I was born on the 2nd of August, exactly 33 years before my father was born. I always taught the fact of sharing the birthday with my dad was something really unique. I don’t even have two friends who were born on the same day.

I never really thought about the math of two people having the same birthday. If one day a friend of mine hadn’t talked to me about the birthday paradox, I probably never would. He said, “You're at a party. There are exactly 23 people in the room, what are the odds of two people sharing the same birthday?” I said, “I don’t know but I think they are pretty low.”

“Actually, it is more than 50%.”

“Shut up! No way that’s true!”

As it turns out, it is.

Introduction

To solve this problem we have to answer a simple question:

How many people do we need to have the probability of two of them sharing the same birthday be more than 50%?

Before we begin we have to make some assumptions. First, we consider a year of 365 days (no leap years, sorry). This means that to have a 100% probability we need 366 people. The second assumption is that all the 365 birthdays are equally likely. In reality, this is not true but the results are affected only slightly. Actually, this is the worst case (learn more know here)

Solution

Let’s start simple. What’s the chance that two people share the same birthday? The first person can be born on any day of the year, this means that the probability is 365/365 = 1. The second person has to be born on the same day as the first and there is a 1/365 chance of that happening.

These two events need to happen at the same time so the probability is:

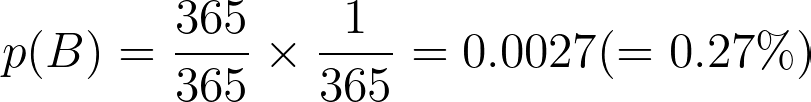
Not very high as we expected.

Now we can consider a group of three people (let’s call them A, B, C). To know the probability of at least two people sharing their birthday we have to calculate:

1. Probability of A and B having the same birthday.
2. Probability of B and C having the same birthday.
3. Probability of A and C having the same birthday.
4. Probability of A, B, and C having the same birthday.

This is not too difficult. However, if we want to do the same for a larger number of people the calculations needed would be too many.

Thankfully, we can use a little trick.

We want to calculate the probability that two people are born on the same day, which we call p(B), but it’s more simple to do the opposite. So we’re going to compute the probability of two people not sharing their birthday, and we call this p’(B).

When we have p’(B), to calculate the probability p(b) all we have to do to get the result is p(B) = 1-p’(B)

Let’s start simple. The probability that two people don’t have the same birthday is p’(B)

The 365/365 term means that the first person can be born on any day of the year. However, if we want that the second person doesn’t share the birthday with the first one, we have to exclude that day from the number of possible birthdays for the second person.

We can do the same for three people and the result is this

You probably already guessed where we’re going with this. If we apply this principle for 23 people the result we get is

This means that the probability of two people not sharing the birthday is 49.3% if there are 23 people.

Now to calculate the probability we simply have to do

There we have it, if we take a group of 23 people, it is more likely that two of them share their birthday than not.

To better visualize the result it is useful to plot in a graph the two probability we have calculated, p’(B) and p(B).

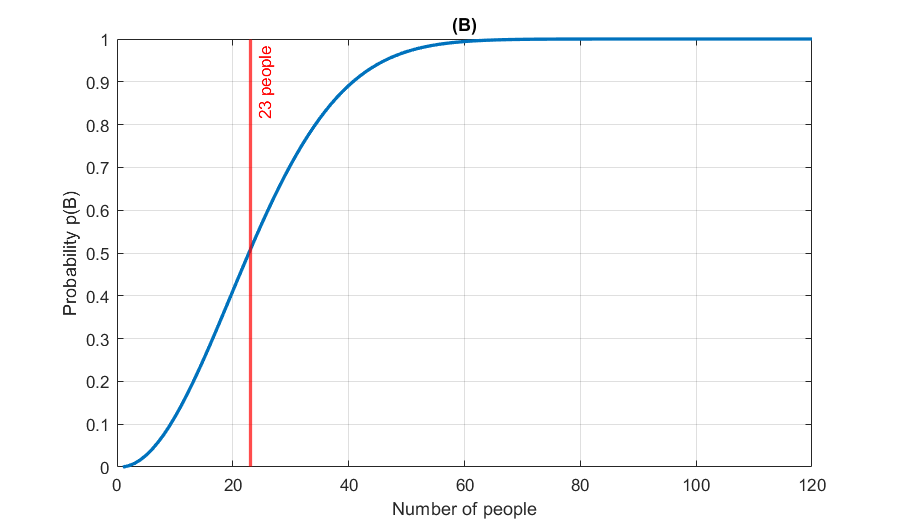
To be more specific, here are the probabilities of two people sharing their birthday:

• For 23 people the probability is 50.7%
• For 30 people the probability is 70.6%
• For 40 people the probability is 89.1%
• For 50 people the probability is 97.0%
• For 75 people the probability is 99.97%
• As the number of people increases the probability gets more closer to 100%. It is exactly 100% for 366 people.

Conclusion

Now you may be wondering why is this problem a paradox. And you would be right because it is not. However, the fact that there's more than a 50% chance that two people are born on the same in a small group of 23 people, is really counter-intuitive.

The main reason is that if we are in a group of 23 and we compare our birthday with the others, we think we're making only 22 comparisons. This means that there are only 22 chances of sharing the birthday with someone.

However, we don’t make only 22 comparisons. That number is much larger and it is the reason we perceive this problem as a paradox.

In fact, the second person was compared with the first one, so he/she has 21 comparisons to make. The third one has to do 20 and so on. To get the total number of comparisons we have to do:

So in total, we make 253 comparisons. Those are a lot more than the 22 we thought we were making at the beginning.

In conclusion, the counter-intuitive nature of this problem is the reason everyone refers to it as the birthday paradox even though it isn’t.