You are probably already somewhat familliar with the notions of entropy and the second law of thermodynamics. These are key concepts in thermodynamics classes, but entropy is a notion that we all struggled with at some points in our studies. Like my statistical physics teacher used to say:

There are only 4 or 5 persons in this world that truly understand entropy, and I don’t belong to them.

— Nicolas Sator —

In fact, in contrast to other quantity in physics such as mass or energy, it seems that entropy is a subjective quantity that depends on the macroscopic variables that an observer chose to define, or has access to. Yet, the second law seems to be a fundamental law driving our universe, on the same level as convervation of Energy. And everytime I was digging deeper into these matters, I was just getting more and more confused…

So, what is entropy ?

Entropy was originally introduced by Clausius in the early 1850s in order to describe energy loss in irreversible processes, which turned very useful topredict the spontaneous evolution of systems (e.g. chemical reactions, phase transitions, etc). But at that time, this was more like an abstract math artifact and there was a lack of formalism that could explain what entropy fundamentally represents. It’s in 1877 that Boltzmann, founder of statistical thermodynamics, proposed an elegant formalization of entropy. Put simply, he defined entropy S as the measure of the number of possible microscopic arrangements (microstates) Ω of a system that comply with the macroscopic condition of the system (observed macrostate), e.g., temperature, pressure, energy:

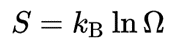
In other words, Boltzmann entropy represents the hidden information of a system i.e., the higher Ω, the less you know about its true microstate. As an example, one of the objects having the highest entropy in the current universe are black hole, as their macrostate are only defined from their mass, charge, and spin. Because we only have access to these variables, there is a very high number of possible ways the matter could be aranged inside it.

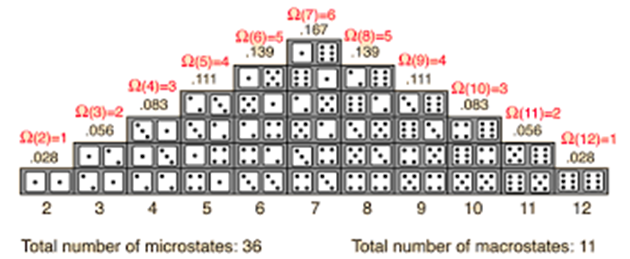
Since the mid-20th century, the concept of entropy has also found applications in the field of information theory and quantum mechanics, but this article is focused on entropy in the context of statistical thermodynamics.

Entropy is not Disorder

One of the most popular belief about entropy is that it represents disorder. It comes from the intuition that what we perceive as “messy” systems generally can take many more possible configurations than ordered systems, which thus have lower entropy. However, as I show you below, the notion of order is subjective and there are several counter-intuitive examples showing why describing entropy as disorder can lead to confusion:

• We usually consider the crystal form of a system to be more ordered than its fluid form. Still, there are few systems that are in a higher entropy state in their crystal form than fluid phases under the same thermodynamic conditions, which goes against the above intuition (see crystalline phases of densely packed tetrahedra [1]).
• Contrary to popular opinion, uniformly distributed matter (which is typically percieved as disordered) is unstable when interactions are dominated by gravity (Jeans instability) and is actually the least likely state, thus with very low entropy. Most probable states, with high-entropy, are those where matter is all lumped together in massive objects.

The 2nd law is just a probabilistic reasoning

A popular statement of the second law of thermodynamics is “The entropy of a closed system can only increase”. However, it is actually not what the 2nd law is about. A correct formulation would be:

When a thermally isolated system has passed from one thermodynamically equilibrium state A to another thermodynamically equilibrium state B, increase of its thermodynamic entropy S is greater than or equal to 0.

The key take-away here is that entropy is not a properly defined quantity outside of thermodynamic equilibrium, a topic still actively debated among researchers [2]. Still, non-equilibirum entropy may be defined in specific systems where we have a set of macroscopic variables that we can continuously monitor at each time point. Then entropy is defined from the number of possible microstate compatible with these macrovariales, and the second principle naturally emerge from a probabilistic reasoning (H-theorm) [3].

A system will spend most of its time in its most probable state, i.e. the ones compatibles with the highest number of possible microstates.

For example, with a simple system of light particles expanding in a box, these macro variables can be the number of particles in each ”grid” of the box. Then, the most probable configurations are the ones with homogenously distributed particles, i.e., with same number of particles in each grid. In order to visualize it, I made a simple simulation with 100 particles starting in a corner and spreading across the room (interacting via Lennard-Jones potential).

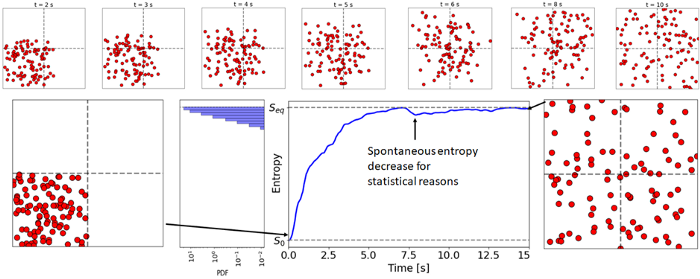
By initializing particles in the corner, the system is starting from a very unlikely state (p = 1/4¹⁰⁰ = 1/10⁶⁰) with low entropy. Then the particles spread in the room and entropy increases quickly. But sometimes, just by chance, more particles will end up in a corner than expected, thus temporarily lowering the entropy (See the fluctuation theorem for a quantitative formalism of this phenomenon). Hence my earlier point about the second law.

Here, I defined some “grids” in order to compute the entropy. There is actually much more complexity on that aspect, for example what happens if you reduce the grid resolution ? How does that change the calculation of entropy ? And how does that generalize to any physical systems ? Check out the second part of this article for a more in-depth discussion.

The arrow of time -> from Big Bang to Heat death

From the second law of thermodynamics follows that the entropy of the universe has been increasing, and will continue to do so, until it reaches thermodynamic equilibrium with its maximal entropy state. Interestingly, this irreversibility creates an asymmetry in the flow of time (in contrast with the 3 spaces dimensions where each direction are symmetric). By going backward to the early time of the universe, one can conclude that it started at an extraordinarily and surprisingly low entropy state [4]. So, how can we explain it ?

Part of the answer is Cosmic Inflation. During its first instants, the universe entered a phase of exponential growth, dominated by a high cosmological constant (~20 orders of magnitude higher than its current value). During that phase, matter was spreading too rapidly for gravity to play a significant role, and thus the maximal entropy state during cosmic inflation was a uniform distribution of matter. However, after roughly 1/10³⁵ seconds of expansion, the universe had grown by a factor of 10²⁶ when the cosmological constant suddenly decayed to its current value and the expansion stopped [5].

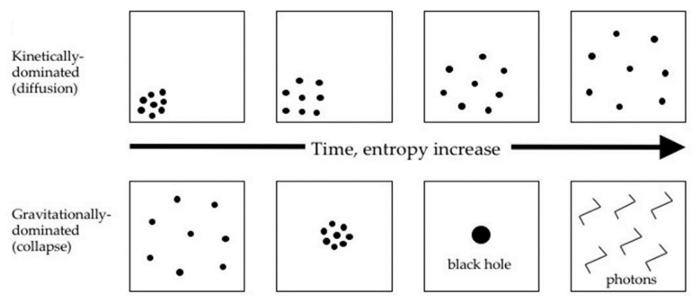
After that event, gravity could finally start playing around and the universe was no longer in thermodynamic equilibrium. Objects started to clump together into what will later become stars, galaxies, and black holes, thus vastly increasing the entropy of the universe (remember, uniformly distributed matter is unstable when gravity is dominant, and thus generally has low entropy).

Regarding the future of our universe, it is just a matter of time before all matter collapse into black holes, which will themselves evaporate via Hawking radiation. It is expected that the last black holes would have evaporated after ~10¹⁰⁰ years. After that point, the universe will mostly consist of photons and neutrinos, very close to its maximal entropy state, typically described as Heat death.

Spontaneous entropy decrease

There is an important subtility to the second law of thermodynamics. As we discussed earlier, on mind-blowingly large time scales, entropy may decrease spontaneously to a low value simply for statistical reasons. For example, the particles in your room could spontaneously end up in a corner if you wait for a very, very, very long time.

Formally, this is known as the Poincaré recurrence theorem, which states that certain dynamical systems will always return to their initial (low entropy) state after a finite time. This does not violate the second principle, which simply states that “A system will spend most of its time in its most probable state”. In other words, over long times, the system will spend only a tiny fraction of its time in one of these low entropy states. Thus, the second law is about statistics, not about deterministic predictions. Still, because the timescales involved in these Poincaré recurrence is typically much larger than the age of the universe, the second law becomes deterministic in practice, and we recover the classical thermodynamics formalism introduced by Clausius and Callen.

Interrestingly, following on the same idea, some formalism of string theory suggest that any macroscopic object of any size could appear spontaneously in vacuum via quantum fluctuation. As an example:

• A Human Body may appear after ~10^(10⁶⁹) years somewhere in our observable universe after it reaches heat death (see Boltzman brain). The same calculation applies for any human sized combination of atoms.
• A New early universe may appear after ~10^(10^(10⁵⁶)) years [6]. By new universe, I mean around 10⁸⁰ atoms being packed in a very tiny volume, thus creating condition similar to our early observable universe in that region.

Boltzmann imagined that our universe could have reached thermodynamical equilibrium and its maximal entropy state a long time ago, but that a spontaneous entropy decrease to the level of our early universe occured after an extremely long period of time, just for statistical reasons. However, the timescales involved in these calculation are so unreasonably large and abstract that one could wonder if these makes any sense at all.

Concluding remarks

Here I tried to provide an intuitive understanding of the entropy and the second law. But actually, several questions were not addressed in this article. For example, when we computed the entropy of these particles expanding in a box, we arbitrarily defined a 2x2 grid to compute entropy. However, we would have obtained different results if we used other grids, or even any other quantity we chose to define. Thus, it seems that entropy is a subjectivequantity that depends on the macroscopic variables that an observer chose to define. So how could we objectively define a set of macrovariables to calculate it?

Actually, digging into this question is quite complicated, and we only scratched the surface. Check out the second part of this article to go more in depth !

Acknowledgements

I thank Bastien Marguet, Hugo Belleza, Clement Quintard and Janos Madar for their valuable remarks, corrections and suggestions, which led to several important edits of this article.

About me

I am a PhD candidate in AI & Healthcare currently working at IBMResearch and I hold a master in quantum physics. In my spare time, I am a blockchain (Web3) developer and the CTO of Peer2Panel, a blockchain startup focused in renewable energy.

I enjoy writing in-depth articles about diverse topics such the Universe, Blockchain and AI. Unfortunatly, writing such articles is quite demanding and I whish I could take the time to write more. If you are thinking about subscribing to Medium and enjoy reading these type of articles, please consider using my referral link ! That would support me directly with a portion of your subscription and incentivize me to write more articles like these. If you do so, thank you a million times!

https://medium.com/membership/@aurelien-pelissier

References

[1] Haji-Akbari, Amir, et al. “Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra.” Nature 462.7274 (2009): 773–777. (https://www.nature.com/articles/nature08641)

[2] Šafránek, Dominik, Anthony Aguirre, and J. M. Deutsch. “Classical dynamical coarse-grained entropy and comparison with the quantum version.” Physical Review E 102.3 (2020): 032106. (https://arxiv.org/pdf/1905.03841.pdf)

[3] Jaynes, Edwin T. “Gibbs vs Boltzmann entropies.” American Journal of Physics 33.5 (1965): 391–398. (https://bayes.wustl.edu/etj/articles/gibbs.vs.boltzmann.pdf)

[4] Egan, Chas A., and Charles H. Lineweaver. “A Larger Estimate of the Entropy of the Universe.” The Astrophysical Journal 710.2 (2010): 1825. (https://arxiv.org/pdf/0909.3983.pdf)

[5] Patel, Vihan M., and Charles H. Lineweaver. “Solutions to the cosmic initial entropy problem without equilibrium initial conditions.” Entropy 19.8 (2017): 411. (https://arxiv.org/ftp/arxiv/papers/1708/1708.03677.pdf)

[6] Carroll, Sean M., and Jennifer Chen. “Spontaneous Inflation and the Origin of the Arrow of Time.” arXiv preprint (2004). (https://arxiv.org/abs/hep-th/0410270)