At a young age a builder taught me how to mark out a right angle using the 3,4,5 triangle rule with a tape measure. That math practicality has stuck with me and recently I have been working to decipher it into its ‘LEGO block’ constituents to increase intuitive understanding.

This post adopts a ‘Tool Kit’ of methods of finding polynomial roots using basic math including Similar Triangles, ‘internal Quadratic architecture’ and formula adaptations and creation of twin function ‘SOSO’ nodes as application points for root approximation methods. Its purpose is to foster intuitive thinking over convenience solutions.

The intention isn’t to beat a calculator. It is to give students confidence to play the function as they see it, to be creative and in the process strengthen their math abilities.

This post assumes math at a high school level.

The Architecture

Consider the following Sextic function:

y= x⁶+x⁵-13x⁴-0.9x³+34x²-14.5x-5.

The 5 Steps to Finding 6 Roots:

1. Find Root B using Similar Triangles , supported by ‘SOSO’, a constructed twin function with Same Opposite Same Opposite +/- coefficients to provide application nodes. Refer to Quintic Polynomials-Finding Roots From Primary and Secondary Nodes; a Double Shot! for an appreciation of the scope of SOSO nodes.
2. Find Root C using the quadratic content to approximate the principal function. Refer to Cubic Polynomials — Managing the Architecture to Calculate Roots, to get the ideas. This also provides an initial application node for Root D.
3. Find Root D using Similar Triangles, a method presented in Cubic Polynomials — Using Similar Triangles to Approximate Roots.
4. Find Root E using a variant of Similar Triangles discussed in The Simplest Cubic Root with a combination of SOSO nodes derived in step 1.
5. Finally Roots A and F are simply downloaded from an Extended Quadratic Equation I presented in Cubic Polynomials — A Simpler Approach which presents in Sextic-Quadratic application as follows:

Where the Factors K, L, M and N represent the known roots.

A, B, are usual x^n coefficients and G the constant=-5.

Step 1 — Root B

Consider the following function y= x⁶+x⁵-13x⁴-0.9x³+34x²-14.5x-5, shown in blue and twin y= x⁶-x⁵-13x⁴+0.9x³+34x²+14.5x-5 derived from SOSO shown in red.

Three Nodes H, V and J are created by the intersection of the SOSO twin and the primary function as follows:

y= x⁶+x⁵-13x⁴-0.9x³+34x²-14.5x-5; subtract the twin.

y= x⁶-x⁵-13x⁴+0.9x³+34x²+14.5x-5 hence:

y= 2x⁵-1.83x³-29x=x(2x⁴-1.8x²-29); solve by standard quadratic equation letting z=x², z=+4.28, from which x=+-2.07. x=0, +-2.07. Hence; Node H=(-2.07, -19.32), Node J=(+2.07, -19.32) and Node V=(0, -5).

To apply Similar Triangles to approximate Root B. We first need to raise Node H above the x axis by see-saw action.

See-Saw Rotation to raise the Node

A) Change the coefficient of x to avoid introducing a constant term into the simultaneous SOSO Quartic function. This see-saws the twin function proportionally with x so it is necessary to divide the required height shift at Node H(x) and reduce the current twin x coefficient F=14.5 accordingly as follows:

B) Reduce coefficient of x by 19.31/2.07=9.33; hence Coefficient F=14.5–9.33=5.17 thereby transposing Node H to (-1.9, 4.07) and Node J to (1.9, -13.68) as shown in Graph 6.

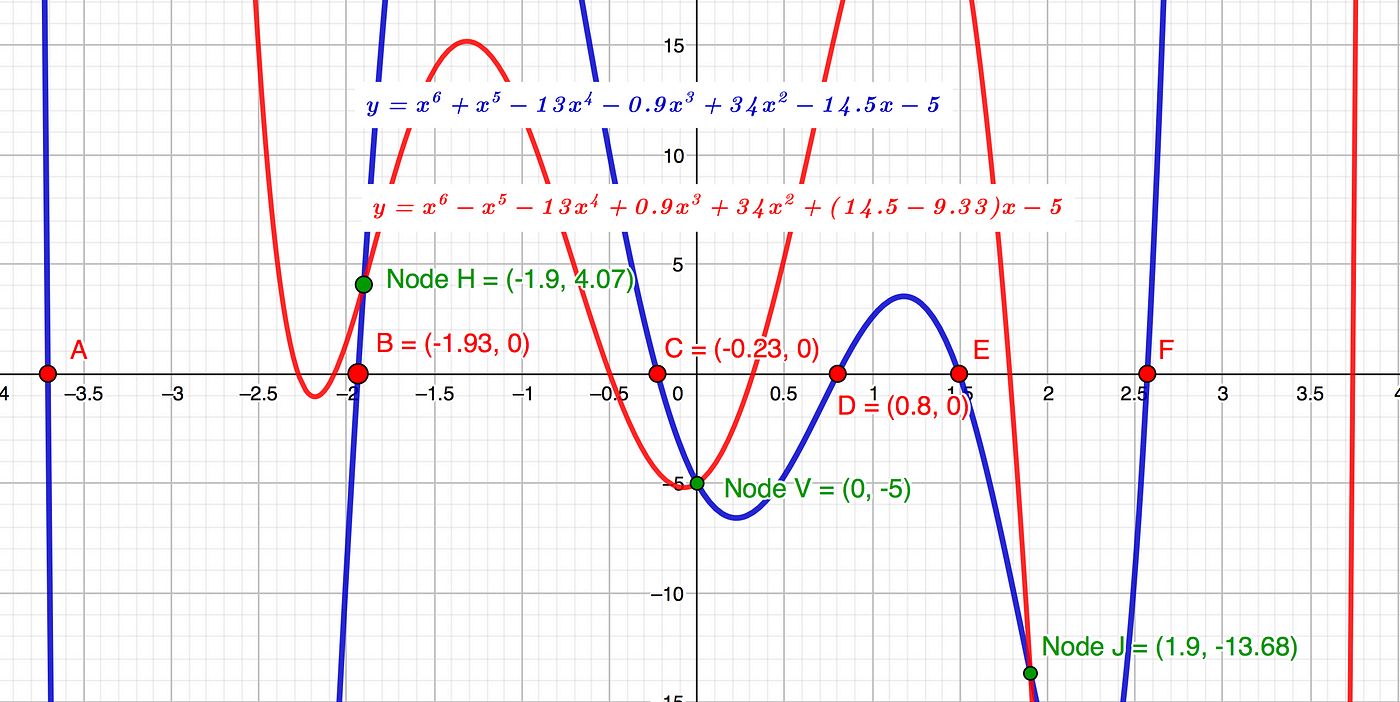
Node H coordinates are again easily calculated by simultaneous equations between the new function: y= x⁶-x⁵-13x⁴+0.9x³+34x²+5.17x-5, and the principal function: y= x⁶+x⁵-13x⁴-0.9x³+34x²-14.5x-5

Hence: y=x(2x⁴-1.8x²-19.67) which can readily be solved by letting z=x².

Hence: x=0, +-1.907 and y=4.07.

Note: there is no known rule to determine a shift that would transpose a node exactly onto the root! The overshoot to y=4.07 occurred because the twin gradient is positive at x=-2.07.

Similar Triangles

Referring to my earlier Post and Diag 1 below, Nodes H and H’ strike a chord across the segment containing the target Root B shown in red.

Node H has transposed from (–2.07, -19.31) to (-1.9, 4.07) hence:

Δx=k*J/(k+m)=4.07*(-2.07+1.9)/(4.07+19.31)=-0.03.

Approx Root B=-1.9+Δx=-1.93, which equals actual x=-1.93.

Step 2 — Root C

Referring to Graph 2 below; separating the function into (a) Sextic-cubic Ya=x⁶+x⁵-13x⁴-0.9x³ and (b) Quadratic Yb=34x²-14.5x-5 shown in dotted black which closely approximates the principal function from the turning point Xtp well through Root C.

The Quadratic equation content directly delivers quadratic Root C=0.23 and also provides Quadratic Root k=0.65 which is the starting point for creation of a Node for application Similar Triangles approximation to Root D.

That was the easy one!

Step 3 — Root D

Referring to Graph 3 below; construct a 1st node intercept on the function using a Sextic-Cubic and Quadratic Contents.

1st Node Intercept

Again consider the Quadratic content Yb=34x²-14.5x-5 with Root K(J)=0.65. Since y=Ya+Yb the Sextic-cubic content Ya=x⁶+x⁵-13x⁴-0.9x³ (shown in dotted green) must intersect the principal function at Node K, where x=0.65. Therefore Ya=-2.4.

2nd Node Intercept

Refer to graph 6

Establish the 2nd node as close as possible to the root with y positive. A simple method is to construct a segment from TP=(0.21, -6.55) through Node K=(0.65, -2.4) and using similar triangles, intercept the x axis at I=(0.9, 0). Use that intercept as a root of the Quadratic content from which the y value of the Sextic-cubic content can be calculated.

Refer to Graph 7

Next calculate the constant shift H of the Quadratic required to create Root I.

Let Yb=34x²-14.5x+H.

Since roots are +0.9 and -0.9–2*0.21=-0.48 as shown at Root J, Constant C=-0.432*34=-14.69. Adding this to Ya=x⁶+x⁵-13x⁴-0.9x³ to maintainy=Ya+Yb we get Ya=x⁶+x⁵-13x⁴-0.9x³+14.69 from which intercept Node K2=(0.9, 1.43).

Using Similar Triangles

Node K has transposed from (0.65, -2.4) to (0.9, 1.43) hence:

Δx=1.43*(0.9–0.65)/(1.43+2.4)=0.09

Approx Root B=0.9-Δx=0.81, compared with actual 0.8.

Step 4 — Root E

Referring to Graph 8, even after the shift to find Root B, the remoteness of Node J=(1.9, -13.68) coupled with its negative twin gradients makes overshoot in 1 iteration for Similar Triangles as used in Steps 1 and 3 too complex so we will adopt a variation for Root E.

In my post The Simplest Cubic Root, Similar Triangles are adopted using a Cubic polynomial Inflection point Ip and the Constant term to construct a triangle hypotenuse which intercepts the x axis close to the target root. Unlike the preceding examples, the nodes don’t strike a cord across the x axis.

In this Sextic example, Node J=(2.07, -19.3) coordinates prior to shift, are to represent the constant term and after shift Node J=(1.9, -13.68), assumed to be proximal to Ip (not defined).

Using Similar Triangles

Δx=0.17*13.68/5.62=0.414.

Approx Root E=1.9–0.414=1.486 versus 1.49 actual.

Note 1: The assumption to use a proximal Ip in this particular case is borne out when it is considered that the worst case scenario for Ip=B<-13.69 results in an approximation A=1.53 as shown in Graph 9 below. This is comparable with a result using Newton’s approximation from Node J=(1.9, -13.68) of;

A=1.9-(-13.68/-37.99)=1.54.

Note 2: Using an Ip value very close to the initial Node J would be akin to using Newton’s approximation from that same point which would not result in a good 1st approximation from either method.

Step 5— Roots A and F by Formula

Given Roots B, C, D and E and their related Factors k, l, m, n, Roots A and F are simply derived from the Extended Qudaratic Equation I presented in an earlier post Cubic Polynomials — A Simpler Approach as follows:

Giving Root A=-3.68 compared with -3.7 and Root F=2.54 compared with 2.57 actual.

I hope this post has shown that even with higher order polynomials, a partnership of node management and basic architectural content can lead to very good results. I have tried to adopt its simplicity, to play with the architecture and use lego block math to solve a complex function with no paternal rules specific to it. Making math work for you, not you for it!