You meet a man on the street. He has two kids. He tells you that one of them is a boy.

What is the probability of the other child being a boy as well?

Before you read on, I want you to think about this problem. Maybe take a pen and a piece of paper and jot down some numbers or calculations. But I encourage you to think about the answer before reading on!

This is your moment to pause before scrolling down!

What answer did you come up with?

If your answer is 1/2, you are correct. If your answer is 1/3, you are also correct.

This may seem surprising and even impossible to you. And it’s the reason why so many people struggle so much to understand probabilities. I recently spent a lot of time discussing this problem with a friend of mine, also a Mathematician after we both confidently answered this question with different answers.

Let’s understand why two answers to the same question can be correct and why it is so important to clearly state the setting when calculating probabilities.

Understanding Basic Probabilities

The most basic and simplest understanding of probabilities is that of a Laplace-Experiment. Our above problem may be modeled as such a Laplace-Experiment.

A Laplace-Experiment is an experiment where all results occur with the same probability. Easy-to-understand examples include rolling a die or throwing a coin.

The first step is always to describe the probability space. We usually use the Greek letter Ω to do this. The probability space is the set of all possible results of an experiment. In the case of rolling one die, Ω is given by

or in the case of throwing one coin, Ω is given by

where 1 stands for “Heads” and 0 for “Tails”. If we throw two coins, we have to differentiate between the two coins and our possible results are given by

Thus, results are tuples such as (1,1) for “heads, heads”, not just simple numbers anymore. Round brackets indicate that the order matters and (0,1) is not the same as (1,0).

Events are any subsets of Ω for which we would like to calculate probabilities. Let’s understand this and first go back to the example of rolling one die.

For example, we may be interested in the probability of getting an even number. We can, therefore, define the event E of all even numbers by

To calculate the probability of this event E, we divide the number of elements in E by the number of elements in the corresponding probability space Ω.

Let’s look at the example of throwing one coin. To calculate the probability of getting the event

we divide the number of elements in H by the number of elements in Ω. Thus, the probability of the event H or “heads” is

With two coins, it becomes slightly more complicated, but not much. What kind of events can we now look at?

We could maybe look at the event where we get two heads

This event has a probability of

We could also look at the event “one head and one tails”

which then has the probability of

Introduction of Conditional Probabilities

Now that we understand how to calculate basic Laplace probabilities, let’s get to conditional probabilities. Formally, the probability of A given B (A under the condition of B) is defined as

where P(A ∩ B) is the probability that A and B are true at the same time. The easiest way to understand is that we reduce our initial probability space Ω to the new and smaller probability space B.

This becomes quite intuitive once you visualize this. A probability for an event A can be interpreted as the size of the area A relative to the area of Ω.

By conditioning to B, we basically make Ω smaller — hence reducing our probability space and now taking the relative size of the overlap of A and B to the area of B. Everything that is outside of B does not exist anymore and B becomes everything.

In Laplace-Experiments we can also see this intuitive explanation in the calculations.

Back to the Initial Problem

Let’s get back to our initial problem and let’s define our probability space first. At first, we only know that the man has two children, i.e. the probability space Ω is given by

where M stands for male kid and F stands for female kid. We use round brackets here because the order of the kids matters. This way, we have a Laplace-Experiment.

We will be interested in the event A that both kids are boys. This event is defined by

Now the man tells us that one of the kids is a boy. This is when the problem becomes interesting. Because of the way this is stated, it is not clear how to interpret this. There are two different options.

Option 1: Does it mean that he points at one of the kids (the first kid) and tells us that this is the boy? Then the event

B₁ = “one of them (the first one) is a boy ”

is given by

Option 2: Or does it mean that he doesn’t point at one of the kids specifically, but just generally tells us that any of them is a boy” because then this event

B₂ = “any of them is a boy”

is given by

We are still interested in calculating the probability of A given B₁ and A given B₂.

Now we can calculate the probability for this event A in both cases. For option 1, the unknown probability is given by

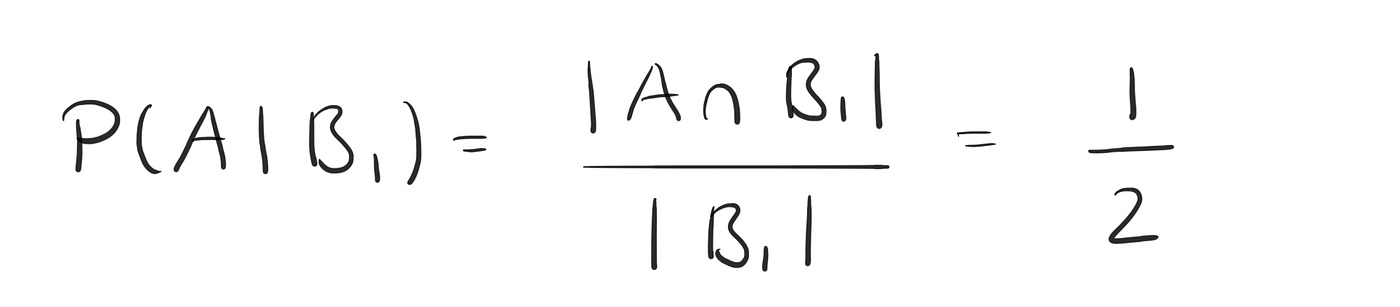
and for option 2, the probability can be calculated by

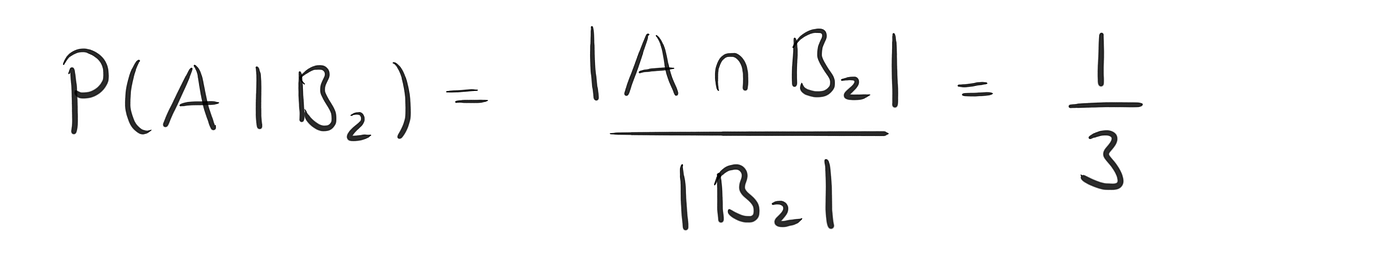
As we can see (and as you probably already expected) — these numbers differ.

This may seem confusing at first because after all — nothing in our setting changed. The only thing that changed was the information we were provided — but in the end, this is the most important part.

Conclusion

This problem came up as a friend of mine (another Mathematician) and I were preparing exercises for some of our students. We had already created a set of questions and were writing solutions.

As we both found this problem trivial, we just jotted down the final answer — except that these answered differed for the two of us.

This sparked a 30-minute discussion on what the right answer is. We came to the conclusion that both are right.

Which answer did you come up with?