Kepler’s Second Law of Planetary Motion, Vector Calculus, and Force of Gravity

Johannes Kepler, the German mathematician and astronomer, is one of the most famous names in astronomy. Kepler formulated three laws of planetary motion based on the precise, detailed and meticulously recorded observations of planetary motion and stars by the great Danish astronomer Tycho Brahe (who collected astronomical data without the aid of a telescope). Kepler worked as an assistant to Tycho Brahe. It took him around 20 years to arrive at the laws of planetary motion. These laws can be stated as follows (source: Wikipedia):

1. The orbit of a planet is an ellipse with the Sun at one of the two foci.
2. A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time.
3. The square of a planet’s orbital period is proportional to the cube of the length of the semi-major axis of its orbit.

Kepler formulated these laws more than half a century before Newton. The concept of gravitational force did not exist at that time. However, if we present Kepler’s second law in terms of the vectors involved and apply the rules of vector calculus, it hints at a presence of a force between the Sun and a planet, which was later called the force of gravitation. Professor Denis Auroux from MIT presents the interesting calculations needed for this ‘vector interpretation’ of Kepler’s second law in a lecture from the course ‘Multivariable calculus’ (I highly recommend this course from MIT OpenCourseWare to all those who are looking for a great online source to learn vector calculus). Let’s go through this exciting application of vector calculus step by step and enjoy its beauty.

Vector calculus and Kepler’s second law

Here is the alternate statement for Kepler’s second law: the area swept out by the line segment joining the Sun and a planet per unit time is constant. Let’s represent this statement using the vectors involved in the planetary motion around the Sun.

Figure 1 shows a planet (the Earth) revolving around the Sun in an elliptical orbit.

r and v represent, respectively, the position and velocity vectors of the planet at a certain point in time. v is always tangential to the orbit. In a short time interval Δt, the planet covers a short distance along its orbit and moves to a new position, where its position vector is represented as r+Δr. Δr represents the change in the position vector in the time interval Δt.

The line segment joining the Sun and the planet sweeps out area (A) of an elliptic sector in the time interval Δt (the elliptic sector is formed by the arc travelled by the planet along its orbit and the line segments joining the ends of that arc to the center of the Sun). According to Kepler’s second law, this area divided by Δt is constant, i.e., A/Δt = constant. This is the mathematical expression for Kepler’s second law.

The area (Aᵣ) of the triangle formed by r, r+Δr, and Δr, which is hatched with red line segments (Fig. 1), approximately equals the area (A) of the elliptic sector swept out by the line segment joining the Sun and the planet in the short time interval Δt. This approximation becomes better for smaller values of Δt. From vector calculus, we know that the magnitude of a cross product of two vectors equals the area of the parallelogram formed by those two vectors. Hence, the area (Aᵣ) of the triangle from Fig. 1 is half the magnitude of any of the following cross products: (a) r × Δr, (b) r × (r+Δr), and (c) (r+Δr) × Δr. Since A ≈ Aᵣ,

For sufficiently small Δt (Δt tending to zero), the directions of Δr and v almostcoincide. Using the definition of v, we can write Δr ≈ vΔt. Substituting for Δr in Eq. (1), and knowing that Δt is a scalar quantity, we get,

According to Kepler’s second law, A/Δt = constant. Hence, Eq. (2) implies,

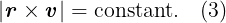
Kepler’s first law implies that the planetary motion is planar. Hence, r and v lie in the same plane, and the direction of r × v is always fixed (r × v always points in the direction perpendicular to the plane of the planetary motion). Since, |r × v|= constant, and the direction of r × v is always fixed,

where C is a constant vector. Hence, differentiating Eq. (4) with respect to time results in a zero vector. Mathematically,

In Eq. (5), dr/dt is written as v (as Δt tends to zero, Δr/Δt = dr/dt=v). aₚ (dv/dt) represents the acceleration of the planet. A cross product of a vector with itself results in a zero vector. Hence, v × v = 0. Therefore, Eq. (5) implies,

Hence, r and aₚ are parallel to each other, i.e., the acceleration of the planet acts in a direction parallel to its position vector.

According to Newton’s second law of motion, F = ma, where F is force and a is acceleration. Hence, in the case of the planet, there must be a force associated with its acceleration. Since the planet rotates around the Sun and does not dash off to infinity, this force must be attractive in nature and directed towards the center of the Sun. This attractive force is the force of gravitation.

Thanks for reading! Constructive criticism and feedback are always welcome!

References:

1. Multivariable calculus, MIT OpenCourseWare.
2. Kepler’s laws of planetary motion
3. Tycho Brahe
4. George Gamow, Gravity, Dover Publications.