Deriving the Quadratic Equation From the Roots Up

An important characteristic of the Quadratic Polynomial y=ax²+bx+c is that it retains its parabolic ax² shape and size wherever it is located in the x-y grid. The other terms, bx +c are just the, “Sit where we say”, ushers!

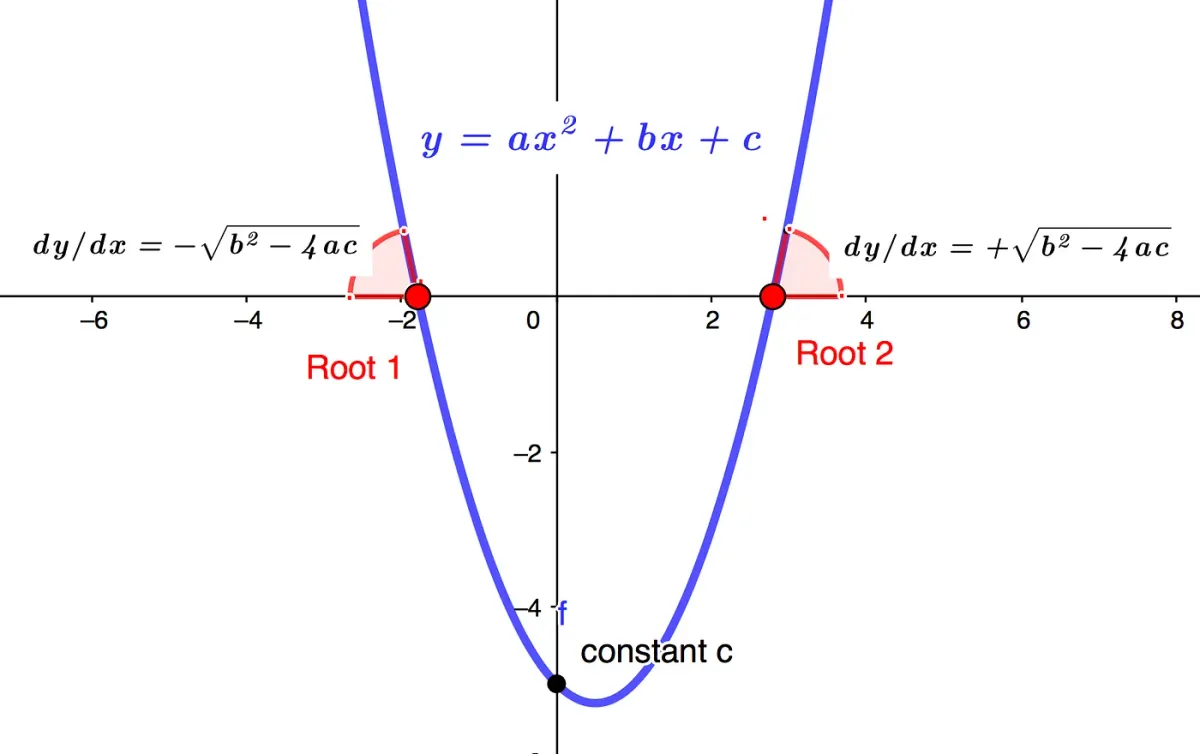
This architectural symmetry and stability means that the gradients at the roots are of equal magnitude and opposite sign and can be used to calculate the roots.

For example, we will show how a quadratic such as y=2x²+x-3 has root gradients:

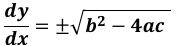
giving dy/dx=+-5, and since dy/dx=4x+1, we can transpose and find x=+1 and -1.5 at the roots!

Accordingly we can proceed to construct the standard Quadratic Equation from the roots up!

This post assumes year 10 or 11 level high school math with the following refresher.

The Standard Quadratic Equation

To begin, let’s remind ourselves of a Quadratic Polynomial, which typically takes the form:

In this, all three terms, ax², bx and c, combine to construct each pixel of the parabolic component ax², in the x-y grid of its graph.

For a detailed review refer to Maths is Graphs — A Visual Perspective.

The roots can be found by use of the standard Quadratic Equation shown below.

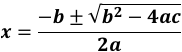
Construction From the Roots Up

Let y=ax²+bx+c hence:

dy/dx=2ax+b, transposing; x=(dy/dx-b)/2a.

Substituting for x in the function y=ax²+bx+c:

y=(dy/dx-b)²/4a+b(dy/dx-b)/2a+c=(dy/dx)²-b²+4ac

Hence, when y=0 at the roots:

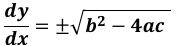
as illustrated in Graph 1:

Since dy/dx=2ax+b, we can substitute for dy/dx and write:

Giving the standard Quadratic Equation:

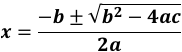
Example: Finding Roots From Gradients

Consider the following Polynomial, y=x²-x-5, shown in Graph 2 below with derivative dy/dx=2x-1 shown at the roots.

Example: y=x²-x-5

Giving: Root 2=2x-1=+4.58; x=5.58/2=2.79 and

Root 1=2x-1=-4.58=-1.79

This post has presented an alternative method for developing the standard Quadratic Equation using the gradients at the roots. It can be intuitively useful in cases where the gradients are an algorithmic design objective and also simply recognising they are the very familiar discriminant.

I hope this post has helped you understand the math behind the formulas and graphs and the Quadratic Equation in a new way. Once again, I have tried to adopt a ‘visual and intuitive’ approach, making math work for you, not you for it!