In Albert Einstein’s original formulation of general relativity (his theory of gravity), the fundamental field is the metric tensor g and the theory is covariant in spacetime. Covariance (more precisely general covariance) “consists of the invariance of the form of physical laws under arbitrary coordinate transformations.” The idea is that since coordinates are only human-made labels, physical laws shouldn’t depend on the way they are chosen.

In general relativity, the action (“an attribute of the dynamics of a system from which its equations of motion can be derived”) is called Einstein–Hilbert action:

where g =det(g), R(g) is the Ricci scalar or scalar curvature, which is roughly a measure of how much the volume of a small ball in a curved manifold differs from the volume of a ball in Euclidean space, G is Newton’s constant and Λ is the cosmological constant or vacuum energy (which I will omit from now on). (note that S should include a boundary integral if the spacetime in question is bounded). For simplicity, let us assume the absence of matter.

Demanding that the variation of this action with respect to the (inverse) metric be zero we obtain Einstein’s source-free field equations:

where R is the Ricci curvature tensor.

An analogy with particle mechanics may help clarify these ideas. In Lagrangian mechanics, we are given a Lagrangian L, we build an action functional S and obtain the equations of motion by extremizing S:

The Goal of This Article

The goal of this article is to show that time is encoded in the geometry of space. The procedure follows the 1962 paper by Baierlein, Sharp, and Wheeler (which I will henceforth call BSW). In the words of the famous book by Misner, Thorne, and Wheeler, Gravitation, “three-geometry is a carrier of information about time”.

This occurs for the following reason. In the extension of the Lagrangian approach in Eq. 3 to general relativity, we will have (see Eq. 4):

• An initial three-dimensional surface with an intrinsic geometric structure (first term of Eq. 4 below).
• A second three-dimensional surface also with an associated intrinsic geometry (second term of Eq. 4).

The goal is to find a four-geometry (the third term of Eq. 4) that satisfies Einstein’s equations (Eq. 2) and reduces to the three-geometries on three-surfaces σ and σ’. In other words, quoting the book Gravitation, “Given the 3-geometries of the two faces of a “sandwich of spacetime”, adjust the 4-geometry in between to extremize the action.” For that, they develop a variational principle (the so-called “condensed thin-sandwich variation principle”) that depends only on the intrinsic properties of the two three-surfaces. Following their procedure we:

• Find the timelike separation between two three-dimensional surfaces (quoting Barbour “how far apart in time” the three-spaces are)
• Find the location of the surfaces in spacetime.

In such four-dimensional spacetime, each three-geometry is well specified based only on the two intrinsic geometries.

Before going any further, it is crucial for the reader to have a notion of the so-called ADM formalism of general relativity. This will be the topic of the next section.

Bird’s-Eye View of the ADM Formalism

In the ADM formalism, named for its authors Ricard Arnowitt, Stanley Deser, and Charles Misner, general relativity is formulated as a dynamical theory (an initial value problem such as described in the two sections above).

The dynamics of general relativity is referred to as Geometrodynamics. As will be shown in this section, the “things that change” in general relativity are distances within three-dimensional surfaces embedded in four-dimensional spacetime (and not the four-dimensional spacetime distances).

In this dynamical version of general relativity, the configuration space is called superspace.

The ADM construction is illustrated below:

The shift vector N, shown in the figure, is a measure of the “distortion of the surface as it evolves with time.” The proper distance between the two surfaces is dτ = N₀ dt where N₀ (or N) is the lapse function. The lapse function measures the rate of change of proper time with respect to the time label of the surfaces Σ(t).

Using Fig. 2, we can re-write ds² using the shift and the lapse (for details see Poisson):

where the tensor g after the second equality is the metric of the three-surface. The extrinsic curvature of the three-dimensional hypersurfaces embedded in the four-dimensional spacetime has the following form

where the symbol “|” denotes the covariant differentiation with respect to the intrinsic spatial metric within the surfaces.

The Ricci scalar R can be written in terms of the extrinsic curvature K, its trace K, and the 3-curvature intrinsic ³R (the 3-dimensional version of the Ricci scalar). Denoting the intrinsic curvature by:

the Ricci scalar can be written as (see Poisson):

The Lagrangian density is then:

The Lagrangian density does not depend on the time derivatives of the shift and the lapse. Denoting by π and dπ/dt the momenta conjugate to N₀ and Nᵢ respectively we find:

Hence, π and πⁱ, the lapse and shift are zero for all times and therefore are not dynamical variables (they are only measurements of deformations of the surfaces Σ). Consequently, we have:

From the H expression:

where we defined:

The tensor G in the first equation is given by:

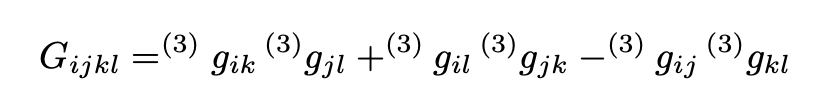
and is called the Wheeler–DeWitt metric.

Finally, using Eq. 11 we obtain the equations of a Hamiltonian dynamical system with constraints, which a reformulation of the Einstein field equations, which describes the evolution of three-metrics:

Paul Dirac, one of the most important physicists of the 20th century, and the American theoretical physicist John Wheeler who was largely responsible for reviving interest in general relativity after World War II were “impressed by the simplicity of the Hamiltonian formulation that he questioned the status of spacetime”.

Dirac declared:

“This result has led me to doubt how fundamental the four-dimensional requirement in physics is. A few decades ago it seemed quite certain that one had to express the whole of physics in four­ dimensional form. But now it seems that four-dimensional symmetry is not of such overriding importance, since the descrip­tion of nature sometimes gets simplified when one departs from it.”

— Paul Dirac (1963)

Wheeler wrote:

“Here the dynamic object is not space-time. It is space. The geometrical configuration of space changes with time. But it is space, three-dimensional space, that does the changing. No surprise! In particle dynamics, the dynamical object is not x and t, but only x… [H]ow can physicists change their minds and “ take back “ one dimension? The answer is simple. A decade and more of work.. has taught us through many a hard knock that Einstein’s geometrodynamics deals with the dynamics of geometry: of 3-geometry, not 4-geometry.”

— John Wheeler (1967)

Using geometrodynamics with the action obtained from Eq. 9, the time evolution of a three-geometry of curved empty space evolving can be determined by giving:

• The geometry of the initial surface (the induced metric three-dimensional hor intrinsic curvature)
• The extrinsic curvature of the initial surface K which describes its embedding in the spacetime to be constructed using Einstein’s equations (see Fig. 3).

However, h and K cannot be specified independently. They must obey the initial value equations of Foures and Lichnerowicz.

The Baierlein, Sharp, and Wheeler Procedure

I will now describe the steps in BSW (following BSW, the prefactor 1/16πG will be omitted).

Step 1

First, choose two very similar (almost identical) three-dimensional metrics:

The time separation between the two surfaces is finite and it is chosen for convenience to be Δx⁰=1.

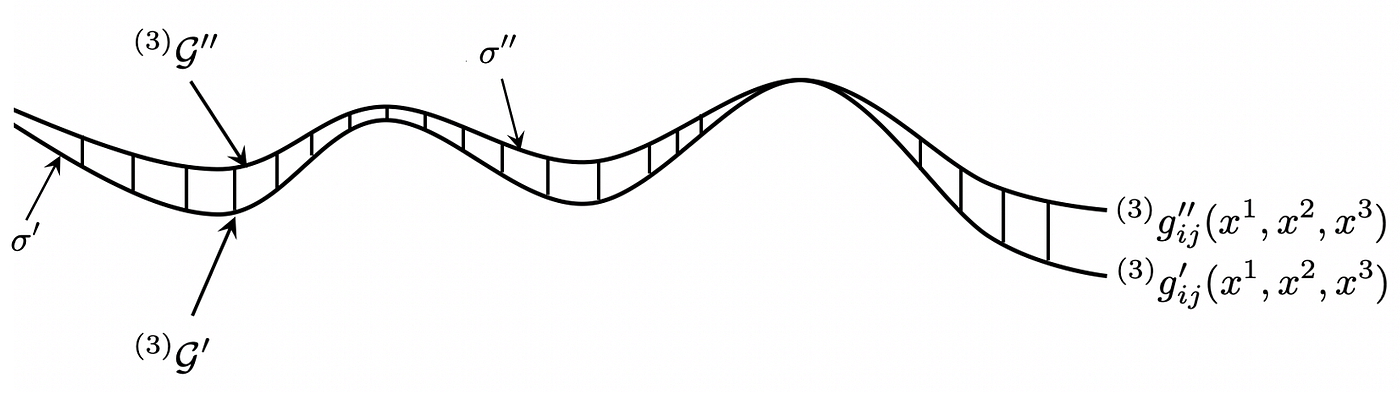
Step 2

The next step is to fill the region between the surfaces with a yet undetermined four-geometry. The separation between two points with coordinates

is given by:

Here η₀ is the lapse function, ηᵢ the shift vector and the first factor of the first term is an average between the metrics of the two three-surfaces.

Step 3

A four-geometry that is an extremum of the BSW action below and has as boundary conditions the geometries of the two three-surfaces will satisfy Einstein’s field equations (Eq. 2).

The action integral is:

In the ADM language it becomes:

The quantity π is the geometrodynamic field momentum conjugate to the geometrodynamic field coordinate ³g defined by:

The vertical bar represents covariant derivatives within the 3-surfaces.

Step 4

Now suppose that the three-geometries are nearly identical. We then have:

Replacing the extrinsic curvature by the following unnormalized time derivative of the three-metric in the direction normal to the surface:

and using Eq. 21, the action becomes:

Step 5

One now extremizes with respect to η₀ and find:

This is the proper time separation between the two three-surfaces.

Step 6

Note that η₀ depends on κ which depends on the shift vector ηᵢ(x¹, x², x³). To obtain ηᵢ(x¹, x², x³), one substitutes Eq. 22 into the action Eq. 23. The result is:

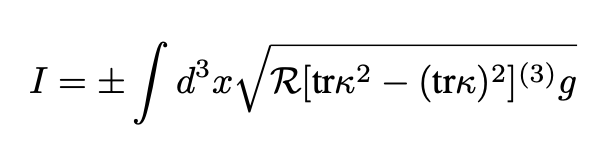
where η₀ was eliminated from the action. One then varies the action I only with respect to the components ηᵢ of the shift vector and obtains three equations of the second order for the ηᵢ.

Step 7

The next step is to solve the equations in Step 6 for the ηᵢ (with appropriate boundary conditions) and substitute them into Eq. 22 and Eq. 24. One, therefore, finds the time separation η₀ in terms of the intrinsic geometries of two three-surfaces.

Step 8

The extrinsic curvature K is obtained from Eq. 22. It can be shown (see references in BSW) that using Einstein’s field equations together with the initial three-metric and the extrinsic curvature K determine (up to a coordinate transformation) the four-metric of the spacetime where the surfaces are embedded.

BSW, therefore, showed how to find the time-like separation between the two surfaces and where they are located in spacetime given the two three-geometries.

Thanks for reading and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin, personal website www.marcotavora.me, and Github have some other interesting content about physics and other topics such as mathematics, machine learning, deep learning, finance, and much more! Check them out!