On September 26, 1905, Albert Einstein’s revolutionary paper Zur Elektrodynamik bewegter Körper (On the Electrodynamics of Moving Bodies) was published in the scientific journal Annalen der Physik (Annals of Physics). In it, Einstein describes his theory of special relativity, which provides fundamentally new definitions of the concepts of space and time. Special relativity reconciles electromagnetic theory (more specifically, Maxwell’s equations) with mechanics by introducing significant changes to Newtonian mechanics for speeds approaching the speed of light.

The Two Postulates of Special Relativity

Special relativity is based on two basic postulates:

• Principle of relativity: The same laws of physics are valid in all inertial reference systems (a reference system not undergoing acceleration).
• Universality of the speed of light: The speed of light in the vacuum, usually denoted by c, is the same for all inertial observers, and it does not depend on the motion of the emitting source.

The first postulate, the principle of relativity, was first enunciated in 1632 by the Italian astronomer, physicist, and engineer, Galileo Galilei (1564–1642) in his book Dialogue Concerning the Two Chief World Systems. The second postulate, the universality of the speed of light, “was Einstein’s great and radical contribution to relativity”.

Relativity of Simultaneity

Suppose we have two events happening in two different locations. The relativity of simultaneity means that, if these events occur simultaneously in a given reference frame, they may not be simultaneous in a different reference frame.

Consider a railroad car, moving at constant speed along a straight track. In the center of the car, a flash of light is given off, and the light spreads out isotropically at speed c. Since the distances between the light source and the two ends of the car are equal, an observer inside it will detect the light reaching the front and back ends of the car simultaneously. However, to an observer outside the car, the two events (the arrival of the light at the front and back ends of the car) are not simultaneous (see the figure below).

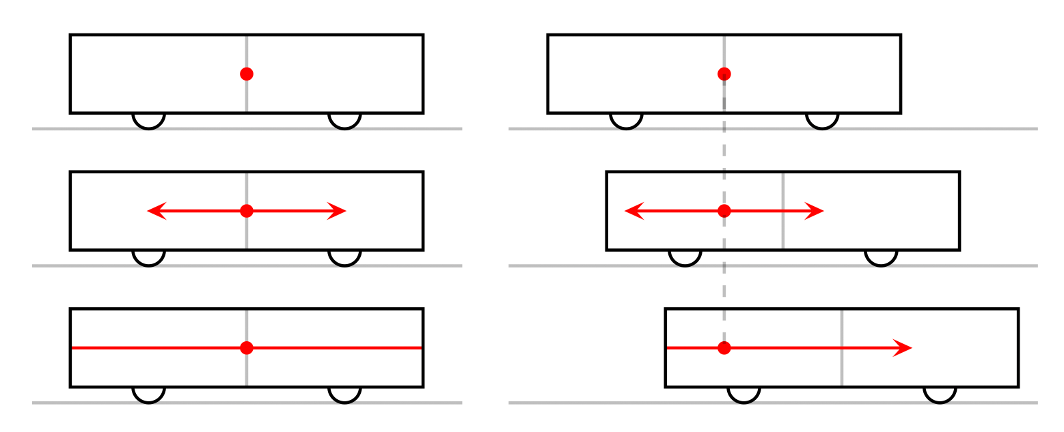
This occurs because, as the light spreads out, the railroad car moves forward, and therefore, from the point of view of the observer outside, the light traveling to the back end of the car has a shorter distance to travel. Since for both observers, the speed of light is equal to c (according to the second relativity postulate), the outside observer will perceive the first event occurring before the second (note that the observers must correct for the time the signal takes to reach them).

Why Clocks in Motion Slow Down

The let us now understand why the slowing of the clocks in a moving system is a direct consequence of the two postulates of relativity.

Consider two mirrors A and B inside a railroad car moving at speed v, and suppose a light pulse coming from mirror A hits mirror B and returns to mirror A. If the distance between both mirrors is L, the time it takes for the light to follow this path is, according to an observer inside the car:

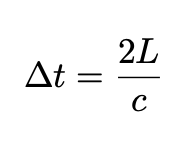
In the reference frame of the observer outside the car, the bouncing light pulse traces out a longer path (the two hypotenuses of the triangles in the figure above). Since, according to the second relativity postulate, the speed of light is constant (equal to c) for all inertial observers, the time the light takes to bounce between the two mirrors, from the perspective of the outside observer, is longer. This implies that, in the reference frame of the outside observer, the clock inside seems to be running more slowly. The time for the light pulse to bounce between the mirrors is then:

To calculate the distance D we apply the Pythagorean theorem:

Using the last three equations we obtain:

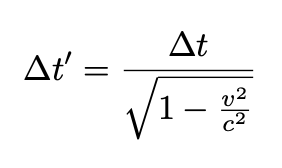
Since the denominator is smaller than 1, this equation shows that the time interval measured by the observer outside the train (which is moving with respect to the mirrors), given by Δt’, is longer than the time interval measured by the observer inside the train (which is at rest with respect to the mirrors), given by Δt. In other words, it takes a longer time for the light beam to bounce between the mirrors in the moving clock than in the stationary one. Therefore, from the perspective of the outside observer, the moving clock runs more slowly.

A fascinating example of the slowing of time with motion is provided by muons in cosmic rays coming to Earth. Muons are produced some 10 km up, at the top of the atmosphere. The spontaneous disintegration lifetime of muons is, on average, equal to 2.2 μs (this is the lifetime in the muon's own reference frame). Due to time dilation, the muons moving very close to the speed of light “live” for a much longer time in our reference frame (the Earth), and that longer time is enough for them to reach the Earth.

Lorentz Transformations

Suppose that the coordinates of an event E in some inertial system S are given by (t, x, y, z). Consider another inertial system S’ where the same event has coordinates (t’, x’, y’, z’). The relations between the primed and unprimed coordinates are called Lorentz transformations and are given by:

Let us now see how the results above can be obtained from the Lorentz transformations.

The Geometry of Spacetime

The geometry of space and time in the special theory of relativity is represented graphically by spacetime or Minkowski diagrams. Spacetime diagrams are two-dimensional graphs with one space and one time dimension. As will be shown below, these diagrams can give a qualitative understanding of the two phenomena we previously discussed, namely, time dilation and the relativity of simultaneity.

Two important concepts are represented in a spacetime diagram:

• An event is an instantaneous occurrence represented by a point (t, x).
• The world line is a line representing the history of the location of an object moving through time.

A spacetime diagram can be used to represent a Lorentz transformation, which relates two inertial reference frames. If an observer at the event (t, x) = (0, 0) (the origin) starts moving along the x-axis, the new time axis t’ and the new space axis x’ of the observer will be inclined with angles smaller than π/4 with respect to the original axes (see figures below). In the reference frame of the moving observer (the primed reference frame), simultaneous events occur in lines parallel to the inclined x’-axis.

Relativity of Simultaneity in Minkowski Diagrams

Consider two events A and B. Their coordinates in the unprimed reference frame (see Fig. 8 below) are:

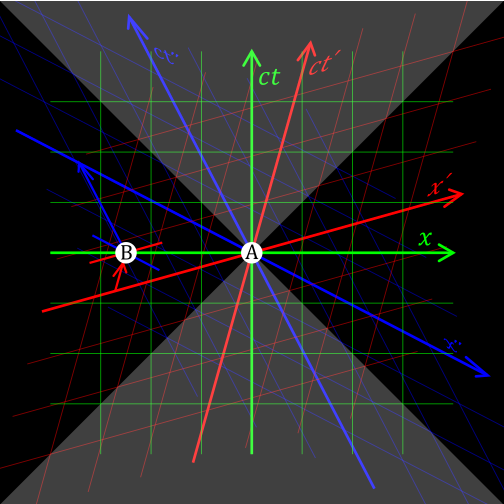
A and B are simultaneous in the unprimed reference frame (they occur at t=t’=0). In the primed reference frame the coordinates of the events are:

Therefore, they are not simultaneous in the primed reference frame. According to the clocks in that frame, B occurred after A. Hence, we see that the relativity of simultaneity can be quickly obtained from the Lorentz transformations.

The figure below shows three events A, B, and C. The moving white line is a plane of simultaneity (the set of events that the moving observer detects as being simultaneous). We see that the order of the events A, B, and C depends on the speed of the plane of simultaneity.

Time Dilation

Consider an observer in the unprimed reference frame at t=0 who examines all clocks in the primed frame. Each clock will read a different time, depending on its position x:

Now let us consider one of the clocks located at some position p. Since we chose one fixed clock, its position x’ in the primed reference frame is constant. To obtain the equation for time dilation we first write the unprimed time coordinate in terms of the primed one. This can be done simply by changing the sign of v in Eq. 5. We get:

Since Δx’=0, Eq. 9 gives:

Hence, as in the case of the relativity of simultaneity, we can straightforwardly obtain the equation for time dilation from the Lorentz transformations.

Thanks for reading and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin profile, my personal website www.marcotavora.me, and my Githubprofile have some other interesting content about physics and other topics such as mathematics, machine learning, deep learning, finance, and much more! Check them out!