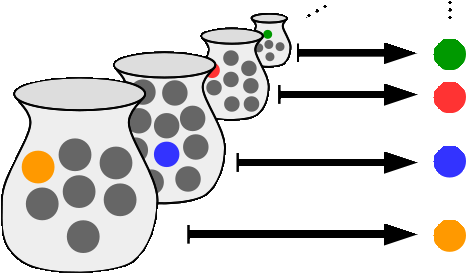
Here’s a fun 2-minute guide to the infamous Axiom of Choice, one of the stranger mathematical curiosities.

What is the Axiom of Choice?

The short answer, not at all rigorous answer, is that the axiom of choice allows mathematicians to extract elements from an infinite number of infinitely large sets at once. This turns out to be very important, because mathematicians are very fond indeed of making infinite-sized things, and even more fond of being able to formalise their manipulations of infinite-sized things.

But let’s dig a little deeper.

The axiom of choice allows us to pick elements from ‘indexed sets’. When dealing with ‘finite things’, this seems kinda obvious. For instance, if A={1,2,3}, B={3,4,5}, and C={5,6}, then it is easy to pick an element from each. Just pick, say, 1 from A, 3 from B, and 6 from C. In fact, if you only every deal with finite sets (e.g. dealing with finite numbers, finite graphs, a finite number of people, etc…), then you will never need the Axiom of Choice. That includes lots of interesting maths, from computer science to graph theory. And it probably includes everything in the real world.

But, Mathematicians don’t want to be constrained to the finite. How very dull it would be if we couldn’t make nearly as many weird and wonderful mathematical objects as our imagination allowed, while keeping coherency through the use of sensible axioms.

Now, imagine we have a bag filled with sets, and there are an infinite number of sets in the bag. The Axiom of Choice tells us that there is a set containing an element from each of the sets in the bag. Basically, this allows us to meaningfully extract elements from infinitely large collections of sets. In fact, it allows us to do this even if each set contains an infinite number of elements themselves! As those sets are often characterised by some property, the elements we get ‘chosen’ for us by the Axiom of Choice will often have structure we can exploit!

Why(!!) the Axiom of Choice?

I start this section with a quote from an answer on MathOverflow, titled “How I Learned to Stop Worrying and Love the Axiom of Choice”. See here.

The universe can be very a strange place without choice. One consequence of the Axiom of Choice is that when you partition a set into disjoint nonempty parts, then the number of parts does not exceed the number of elements of the set being partitioned. This can fail without the Axiom of Choice.

*That answer was written by the mysteriously named Dr strangechoice*

What does this mean? It means that you can take a set, distribute all of its elements into different parts, and end up with more parts than you have elements. Imagine taking a set of different sweets, all of different colours, putting two in each bag, and ending up with more bags than sweets!

Without the Axiom of Choice, a lot of things fall apart, and rather quickly.

We require the Axiom of Choice to determine cardinalities. If you remove the Axiom of Choice, then it is consistent that the real numbers can be written as a countable union of countable sets.

What if we want to sensible deal with ‘large’ vector spaces. In R³ we can construct a ‘basis’ for the space, so that any point can be written as a linear combination of 3 components (e.g., 3 across , 2 up, 4 along, where ‘across’, ‘up’, ‘along’ are our ‘basis’). This requires a Hamel basis, (which I constructed here during lockdown), which is the equivalent of a basis from our standard 3-Dimensional space, but for an infinite-dimensional vector space.

Oh, and it is possible that the reals can be written as the union of two sets which are smaller cardinalities. That’s basically heresy! This would make a nonsense of comparing the sizes of infinitely large sets.

Is the Axiom of Choice even true?

… is the wrong way to look at it.

It has been proven that the Axiom of Choice is consistent with the other axioms of set theory, but so its negation. I.e. we don’t need to worry about it messing up our consistency with the apparatus we use for finite sets.

The Axiom of Choice extends what we are comfortable doing with finite sets, is consistent with the other axioms, and makes a vast amount of mathematics work, and much of this mathematics is extremely useful.

If you are looking for some kind of Platonist truth, then I think you are barking up the wrong tree. It is better to view mathematics as structure, much of which parallels the real world (such as Euclidean geometry giving real insights into objects which aren’t actually 2D and have perfectly smooth edges), rather than necessarily being some necessarily true statements.

It works and underpins the mathematical objects we use to talk about probabilities, particle physics, and more.

Jerry Bona put it: “The Axiom of Choice is obviously true, the well-ordering principle obviously false, and who can tell about Zorn’s Lemma”. The *joke* is that these three principles all imply each other; yet mathematicians have very different intuitions about whether they should be true.

In any case…

In any case, I’ve ‘stopped worrying, and learned to love the axiom of choice’. Perhaps when in a few years after learning more about the foundations of mathematics, I’ll be sufficiently spooked out to reconsider :)

P.S. If you’re interested in this kind of mathematics, I wrote a short intro to the (in)famous Zorn’s Lemma. Also, if you would like some random mathematical updates, you can follow me on twitter, where I am ethan_the_mathmo. If you have thoughts and/or corrections please leave them below. I think I manage to respond to 85%ish of comments and try to update articles if mistakes are spotted.