What Did Newton Do with his Time During Quarantine?

Similar to the colleges and companies that recently sent people to their homes due to the coronavirus pandemic, Trinity College, Cambridge, sent Isaac Newton to his home in Woolsthorpe Manor during the Great Plague of London (1665–1666), while he was only at his early 20s. Newton spent 2 years at his home, where the famous apple tree is located now.

Although his professors were not there to guide him, Newton continued his studies on mathematics and optics. His incredibly productive year of quarantine, 1666, is now referred to as his “annus mirabilis”, meaning the year of wonders.

As a reference to Newton’s annus mirabilis, the year when Einstein published four papers that changed modern physics, 1905, is also called Einstein’s annus mirabilis, the miracle year.

During his time at quarantine, Newton did groundbreaking discoveries on mathematics, which are now the fundamentals of calculus. The question of who discovered calculus first is a controversy since at the same time with Newton, Gottfried Wilhelm Leibniz also discovered calculus with the notation that we use frequently today. I included a letter from Newton to Leibniz at the end of this story to give you a better understanding of their relationship.

Let’s look at Newton’s notes on “the method of series and fluxions”, which is now called Calculus, to understand him and his discovery better.

In his notes, Newton uses the letter “o” to describe an infinitesimal change in time, which now we refer to as “dt”, the velocity in the x-direction as “p”, and the velocity in the y-direction as “q”. Therefore, he represents a particle’s change in location as below. Note that “ad” is the new x-coordinate and “bh” is the new y-coordinate.

Newton then makes a demonstration on taking the time derivative of an equation, which is basically the differentiation we use today. He first replaces the x and y terms with the terms that he showed above, (x + po) and (y +qo).

Here, Newton draws a line through the number “0” at the end of the equation to make sure that it is not confused with the letter that he uses to represent a very small change in time, “o”.

Then, he uses binomial expansion to expand his equation.

Then he cancels out the following terms because, from Equation 1, he knows that they are equal to zero.

Then he divides every term by “o”. He can do this because “o” is not zero, but close to zero.

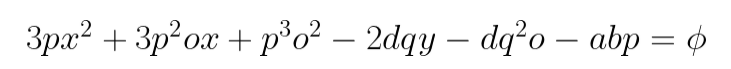
Now, he gets rid of all the terms that have “o” in them, because “o” is so small that these terms will not contribute to the result. However, at this point, you may realize that Newton treated “o” as if it is zero and as if it is not zero at the same time. At his time, this was very controversial, but today we use the idea of limits to do the same thing.

Finally, he gets the result in Equation 5, which is what we would get if we did implicit differentiation by taking the time derivative of Equation 1. Here is the modern-day version of the time derivative of Equation 1:

As you can see, the velocity p stands for (dx/dt) and the velocity q stands for (dy/dt).

This was Newton’s work on differentiation, but later he also talks about integration and The Fundamental Theorem of Calculus. During his times of quarantine, Newton also does very important work on optics by demonstrating that white light is heterogeneous though separating it by refraction. Newton was so devoted that he almost blinded himself while doing his optical experiments.

Now, we can take a look at his letter to Gottfried Wilhelm Leibniz.

Although this letter is in Latin, a part of it would not be meaningful to a person who knows Latin as well, because Newton, concealed a part of his letter to Leibniz by using a code to make sure that Leibniz doesn’t steal his work. Newton writes,

“the basis of these operations, sufficiently obvious (since now I cannot continue my explanation) I have thus rather concealed 6a 2c d æ13e 2f 7i 3l 9n 4o 4q 2r 4s 9t 12v x.”

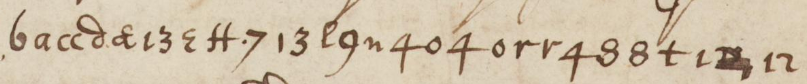
The enciphered sentence was later decoded by Wallis as “Given any equation, involving fluent quantities, to find the fluxions, and vice versa,” which is Newton’s way of stating The Fundamental Theorem of Calculus.

Sources

Brockell, Gillian. “During a Pandemic, Isaac Newton Had to Work from Home, Too. He Used the Time Wisely.” The Washington Post, WP Company, 12 Mar. 2020, www.washingtonpost.com/history/2020/03/12/during-pandemic-isaac-newton-had-work-home-too-he-used-time-wisely/.

From the Letter of Newton to Oldenburg (to Be Forwarded to Leibniz) of October 24, 1676. L. T. Moore, Isaac Newton. A Biography, Dover, NY, 1934., www.math.purdue.edu/~eremenko/dvi/newton.pdf.

JCU Collection Services, and Post. “Isaac Newton’s ‘Year of Wonders’ 1665–1666.” JCU Library News, jculibrarynews.blogspot.com/2020/04/isaac-newtons-year-of-wonders-1665–1666.html.

Levenson, Thomas. “The Truth About Isaac Newton’s Productive Plague.” The New Yorker, The New Yorker, 7 Apr. 2020, www.newyorker.com/culture/cultural-comment/the-truth-about-isaac-newtons-productive-plague.

“Newton Papers.” Cambridge Digital Library, cudl.lib.cam.ac.uk/.

“The Newton Project.” The Newton Project, www.newtonproject.ox.ac.uk/.

Tibees. “Newton’s Quarantine Notes That Changed Math Forever.” YouTube, 23 May 2020, www.youtube.com/watch?v=M6g-sR-lRCU.