What is Wave-Particle Duality?

One of the most well-known ideas in quantum physics, and one of the ideas most frequently held up as an example of the mysterious nature of quantum physics, is that material objects exist simultaneously as particles and as waves. Material objects exist as particles in the sense that they can be assigned definite quantities like location and momentum, but they also exist as waves in the sense that they can be described as a propagating disturbance in some underlying (possibly very abstract) field.

In this article, I’ll explain what this actually means.

The wave nature of light

It’s interesting to note that the very first people in history to attempt a study of the nature of light, those being the ancient Greek and Indian philosophers who lived around 500 BCE, believed that light was a stream of infinitely small particles. It’s also interesting to note that philosophers in these two civilizations reached the same conclusion completely independently of each other. However, these conclusions were completely pre-scientific, being motivated by philosophical and metaphysical ideas.

Rene Descartes (1596–1650) is generally credited as the first scientist to offer the correct view. Descartes compared what was known at the time about the propagation of light to what was known about the propagation of sound, which was known to be a wave, and concluded that light propagates from a luminous source because of a disturbance that the source causes in a transmitting medium.

The failure to actually identify this medium was the main point of contention among scientists in the debate that took place over the next 200 years over whether light was composed of particles or waves. During this period, Isaac Newton may have been the most famous supporter of the particle theory of light, although he conceded that individual light particles could interfere with each other like waves when they collided, and due to Newton’s fame this view dominated for almost a century.

But as optical instruments became more sensitive over time, evidence continued to mount that light does indeed propagate as a wave rather than a stream of particles. The final nail in the coffin for the particle theory came in 1802 when Thomas Young performed his famous double-slit experiment.

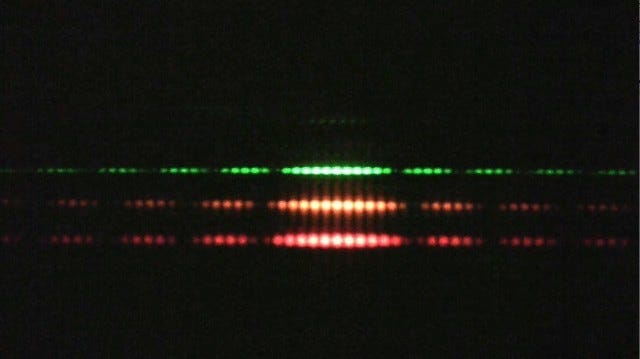
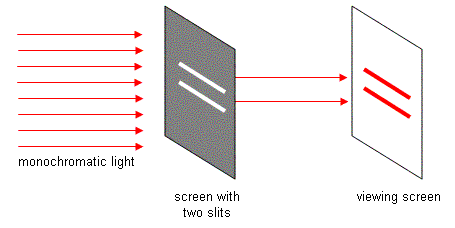
In this experiment, now a mainstay of physics lab classes for college freshmen, light is incident on a barrier with two very narrow slits cut into it, and these slits are separated by a very short distance. The light that passes through the two slits and shines on a screen some distance past the barrier. If light is composed of particles travelling in straight lines, then we should see two bright lines on the screen behind the slits:

But in fact this is not what happens! Instead, one observes a pattern that looks something like this:

The only difference between the modern physics classroom version of the experiment and the one originally conducted by Young is that Young used natural light whereas we use lasers, since they produce coherent and monochromatic light, and that’s a little easier to work with.

Notice the alternating bright and dark spaces. Young argued that this occurs because of constructive and destructive interference. The source is placed so that light waves reaching the two slits are in phase with each other. However, since the two slits are separated, light from each slit has to travel a slightly different distance to each point on the screen, so the travel time of the waves is slightly different, and therefore the two waves reach each point at different phases. At a point on the screen where two waves arrive π radians (180 degrees) out of phase with each other, they destructively interfere and that point appears dark.

To make this clear, let’s try to use Young’s argument to derive a formula for which parts of the screen should be bright and which should be dark and see if that formula matches our observation. To do so, we will find a formula for the phase difference Δϕ as a function of position x along the screen. We will do so by considering the difference in the lengths of the two paths S₁P and S₂P, which we will call ΔL, for each P as a function of x. Assume also that the distance D from the barrier to the screen is much greater than the values of x that we are interested in and the slit separation d. The angle θ is the angle at A, the midpoint of the two slits, of the triangle P₀AP.

Start by drawing a circle centered at P which passes through S₁ and intersects S₂P at point B:

Since B and S₁ are points on the same circle, S₁P and BP have the same length, so the path difference we are looking for is the length of S₂B. Consider the point C chosen so that S₁C makes a right angle with S₂P:

Notice that the length of BC is quite short. If this diagram was drawn to scale then this length would be very nearly zero, so I will approximate the desired length difference as the length of S₂C. Since one of the side lengths of triangle S₁S₂C is given as d, I need either the length of S₁C or the measure of angle ∠S₂S₁C to find the length of S₂C.

Since D is much greater than x, θ is a very small angle. Since S₂C is also very small, so is the angle ∠S₂S₁C. We will assume that these two angles are approximately equal by order of magnitude estimation, justified by the fact that S₂C and θ both approach zero proportionally to 1/D as D goes to infinity.

All of this means that I can approximate the path difference by dsinθ. One could make a more sophisticated justification for this approximation by calculating S₂B explicitly by going through all of the trigonometry and then approximating, and this would probably be a useful exercise for anyone planning to take an advanced course in optics, but for the purposes of this article it’s not worth the extra time.

The time that it takes for a wave to travel from S₁ to P is t₁=|S₁P|/c, so if the wave has angular frequency ω then the phase when it reaches P is ω|S₁P|/c, and since the distance from S₂ to P is dsinθ, this means that the phase of the wave from S₂ when it reaches P is (ω/c)(|S₁P|+dsinθ) so the phase difference at P is Δϕ= (ωd/c)sinθ=(2π/λ)dsinθ. Now we need to do just a bit more work to find the brightness at P. It turns out that the irradiance, and therefore the brightness, of two equal interfering beams at a point is given by:

Obviously the waves being emitted from S₁ and S₂ are not beams, but since we are only considering the intensity at a single point, we can pretend that they are. Because the distances from these two sources are slightly different, the amplitudes will not be exactly equal, but since the distance is very small it’s fair to approximate the two beams as having exactly the same amplitude I₀ at P. Our hypothesis that light is a wave carried by the electromagnetic field will be validated if I, as a function of x, predicts the locations of the dark spots:

In the second line, I used the fact that tanθ=x/D and θ is very small since D is much greater than x and tanθ≈sinθ for very small angles. This formula predicts that we should have peak brightness at x=0, regularly-spaced dark spots occurring when dx/λD is equal to ±1/2, ±3/2, ±5/2, and regularly-spaced bright spots occurring dx/λD is equal to ±1, ±2, ±3, etc. This matches what we see on the screen in the experiment.

This formula only predicts the location of the bright spots, and not how bright they actually are. Notice that in the picture, what we actually see are “blocks” of alternating bright and dark spots separated by large dark intervals. Our formula for I(x) doesn’t predict this behavior because we didn’t consider single-slit interference phenomena, where the light coming from each slit interferes with itself as well as with light from the other slit. If we took this into consideration, then we would see our formula for I(x) scaled by what’s called the single-slit envelope:

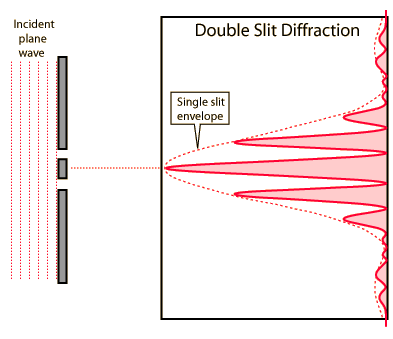
In any case, since single-slit interference is a behavior of waves, this only provides further evidence for the wave theory of light. Word of Young’s result spread quickly and within a few years the scientific community had overwhelmingly accepted the conclusion that light was a wave. The theory of the wave nature of light withstood every challenge thrown at it, and any remaining holdouts were silenced in 1873 when Maxwell’s theory of electromagnetism was validated by experiments conducted by Heaviside and Hertz, including the prediction that electromagnetic radiation behaves exactly like light.

There were just two remaining problems that the classical electromagnetic theory of light couldn’t seem to solve, and the answer eluded scientists until 1905.

The photoelectric effect and the particle nature of light

When monochromatic light of sufficiently high frequency is incident on a metal surface, electrons will be emitted from that surface. It was understood by 1900 that this was occurring because electrons were absorbing enough energy from the radiation that they started to move fast enough to escape from the metal surface. Something odd was happening, however:

• Electrons started to eject from the surface instantly when the light was turned on, regardless of the intensity of the light.
• The kinetic energy of the emitted electrons depended only on the frequency of the light and not on the intensity, though light with greater intensity causes more electrons to be ejected.
• Below a given frequency threshold, no electrons would be detected at all.

When one plots the kinetic energy of the electrons for different metals, one obtains a graph like this:

By fitting the data, one obtains the function K=hf-φ where h is Planck’s constant and φ is called the work function of the metal.

This was at odds with the classical electromagnetic theory, which would imply that:

• The kinetic energy of the emitted electrons should depend only on the intensity of the incident light and not on the frequency, since more brighter light delivers more energy per unit time.
• We should not observe any cutoff, since even if the light intensity is low, the electrons will just slowly absorb energy until they have enough to escape. This also means that there should be a lag time since the electrons will take time to absorb enough energy.

In 1905, Albert Einstein published a paper titled “On a Heuristic Viewpoint Concerning the Production and Transformation of Light” in which he proposed a solution to this problem. This paper later earned him the Nobel Prize in Physics in 1921. The solution came from a surprising source.

Any object with a temperature above absolute zero loses energy by thermal radiation. This is called black-body radiation. A black body is an ideal object that does not reflect any incident radiation, so any radiation detected from a black body must be thermal radiation. A nearly-ideal black body can be constructed by heating a hollow spherical shell made of an insulating material like clay to a very high temperature and poking a tiny hole in it, this hole will be the black body since any radiation incident on the hole is unlikely to be reflected back out. When one measures the frequency spectrum of the radiation coming out of the hole, the graph of the result will look something like this:

There was a problem, however. The classical theory predicted the frequency spectrum curve would become infinite for high frequencies. Not only did this completely fail to match the experimental results, but it also would mean that all matter in the universe would radiate all of its stored away in an instant.

In 1900, Planck was able to derive a formula that gave the correct answer by supposing that thermal energy was absorbed or radiated in discrete amounts, called “quanta”, although he stopped just short of attributing this to actual particles of light. Essentially, Planck’s construction treated the radiation field inside the cavity as a system of harmonic oscillators spontaneously exchanging quanta of energy back and forth with the atoms of the cavity walls, with some of that energy being spontaneously radiated out through the hole.

Einstein took this basic idea further and proposed that, in fact, light could actually act like a stream of particles. His model explained the photoelectric effect by proposing that energy was being delivered to the electrons by particles of light, later named photons, with energy E=hf colliding with the electrons. Each photon collides with exactly one electron and gives up all of its energy. This would mean that:

• If the incident light has lower intensity then this just means fewer photons, but the energy of the photons depends only on the frequency. This explains why the energy of the ejected electrons depends only on the frequency of the light, since the intensity of the light only describes how many photons collide with the metal and therefore how many electrons are ejected, but not the energy of those ejected electrons.
• We should not expect there to be a lag time because the collision process is instantaneous. A photon collides with an electron, instantly giving it enough energy to escape. There is no process by which the electron slowly absorbs energy from the field until it has enough to escape.
• If the energy of the photons is less than the work function, then what happens is a photon hits an electron, raises its energy state by a little bit but not enough to escape from the metal, and the electron will spontaneously radiate away the extra energy and drop back to its ground state without leaving the metal. Although it’s possible in principle for a second photon to hit the excited electron and then giving it enough energy to escape, it turns out that the time it takes for the excited electron to spontaneously drop back to ground state is so short that it’s extremely unlikely for another electron to strike it while it’s excited.

This discovery surprised and fascinated the scientific community. Then in 1921, Einstein’s hypothesis was completely validated by results in Compton scattering, which found that collisions between electrons and photons behaved like collisions of particles. It seemed as though light somehow acts like both a particle and a wave. How could this be?

As if that wasn’t mysterious enough, a few years later, things got even weirder.

The wave nature of matter

Between 1921 and 1925, scientists Clinton Davisson and Lester Germer had been performing a series of experiments to use electron beams to analyze the surfaces of fragments of nickel. Their hypothesis was that the rough surface of the nickel would scatter electrons and they hoped to obtain information about the surface features of the nickel samples by analyzing the scattering.

In the experiment, an electron gun bombards the nickel surface with a beam of electrons, and a detector is used to measure the number of electrons reflected at various angles. The experiment has to be performed in a vacuum tube because free electrons can only travel a fraction of a micrometer in air before losing all of their energy to collisions with air molecules.

To Davisson’s dismay, the initial trials revealed nothing interesting about the surface of the nickel sample or the structure of nickel atoms. It turned out that the roughness of the crystal surface at the molecular scale caused electrons to be scattered in random directions . But then something strange happened in 1925.

During one experiment, an accident caused a breach in the tube, and the air caused the surface of the nickel sample to oxidize. To remove the oxide layer, Davisson and Germer heated the sample in a high-temperature oven. When they next performed the scattering experiment, they suddenly noticed strong peaks in scattering intensity at certain angles.

The purple curve in these pictures shows the scattering intensity at various angles, and the black arrow represents the incident electron beam. (To visualize more clearly, imagine a straight line originating at the point of incidence drawn to each point on the purple curve). The first picture shows an early result. The second picture shows a result from an experiment in 1925 before the tube failure. The third picture shows a result from after the tube was repaired.

What was going on there?

The first thing that Davisson did was have the nickel sample analyzed by microscopist F.F. Lucas. Lucas found that the sample had adopted a regular crystal structure.

Like most metals, the molecular structure of nickel is polycrystalline at room temperature. This means it can be thought of as a jumble of tiny, randomly-oriented crystalline domains called crystallites or grains.

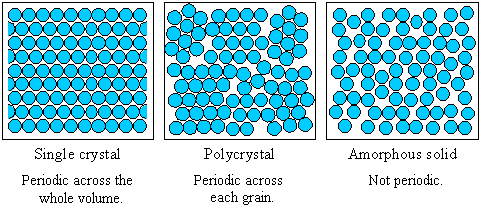
When heated at high temperature, however, these polycrystalline grains can align themselves into a single monocrystal structure. Davisson’s new result must have had something to do with this new crystal structure. However, after a few more months of experiments with specially prepared crystalline nickel samples, he couldn’t figure out exactly what.

In 1926, Davisson attended the Oxford meeting of the British Association for the Advancement of Science. There, he learned of de Broglie’s recent hypothesis that electrons could behave like waves and, to his surprise, Max Born delivered a lecture in which he cited Davisson’s anomalous result as evidence for de Broglie’s hypothesis.

According to Born, a process was occurring in which electron waves were scattering off of parallel crystal surfaces in a process similar to Bragg diffraction. In Bragg diffraction, parallel x-rays incident on a crystal surface pick up a path difference when they reflect off of atoms in parallel crystal layers:

Just like in the double-slit experiment, this causes the two waves to have a phase difference when they reach a detector, causing constructive or destructive interference at that point.

Davisson pursued this line of inquiry over the next few years. This culminated in a 1928 paper “Reflections of Electrons by a Crystal of Nickel” in which Davisson and Germer reported that, although the diffraction process did not exactly match Bragg diffraction (which they found by using electrons with 54 eV of energy, which by de Broglie’s law would have the same wavelength as an x-ray), there was a clear formal analogy between the two processes. For this work, Davisson was awarded part of the 1937 Nobel Prize in Physics, along with G.P. Thomson (son of J.J. Thomson, discoverer of the electron) who had been carrying out similar experiments.

This conclusively proved that electrons behaved like waves. Similar experiments were performed with other experiments, with similar results.

And although by 1961 the question was completely settled, just for good measure, an electron double-slit experiment was performed by the German physicist Claus Jönsson of the University of Tübingen, which also found a double-slit interference pattern exactly like what was found by Young. A particularly famous picture of the electron double-slit interference pattern was produced by Tonomura et all, working for Hitachi in 1989:

This experiment is particularly interesting because it explicitly shows the interference pattern building up from individual electrons. By 1989 it had been known for decades that this would happen, but this appears to be the first reported instance of this being observed directly.

Explanation: Schroedinger’s Equation.

Okay, so now instead of talking about the quantum physics, I’ll actually show you the quantum physics. I’m going to stick to the electron wave problem here because extending this reasoning to photons means getting into quantum field theory, which I don’t think is appropriate for the level of this article. However, the underlying ideas are the same.

In quantum mechanics, we postulate that particles are waves in the sense that there is a function ψ, which is generally complex and depends on position and time, called the wave function or probability amplitude which has the properties that:

• The integral of |ψ|² over all of space is finite.
• The integral of |ψ|² over a particular region of space V divided by the integral of |ψ|² over all of space gives the probability of detecting a particle in region V.

If the particle is not subject to any time-dependent interactions, then ψ is a function only of position which satisfies the time-independent Schroedinger Equation:

Where m is the mass of the particle, ħ is Planck’s reduced constant, V(r) is the potential field (if any) that the particle is interacting with, and E is the particle’s total energy. Note that even if there isn’t an explicit time dependence, we still have to include a phase factor exp(-iωt) so that the full wave function is:

Since |exp(-iωt)|=1, the phase factor vanishes when we compute the probability. Note that ω=E/ħ. In general, we obtain an entire family of solutions

In general, the solution is actually a linear combination of possibly infinitely many solutions ψₙ with energies Eₙ:

Where the cₙ are such that |cₙ|² is the probability of the system to being observed to have energy Eₙ when the energy is measured. If we happen to know for certain that the energy is E, (for example, by taking a measurement, or by deliberately preparing the system with this energy), then the wave function “collapses” down to the aforementioned form:

Observe that when V is zero, corresponding to the situation where the particle is propagating in free space, the equation takes the following form:

For example, this could describe the situation where electrons are freely propagating in a cathode ray tube. By comparison with the one-dimensional version of this equation:

whose solution is:

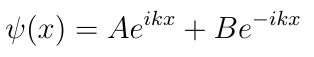
We see that the solution has the form:

The vector k is called the wave vector:

The wave vector tells us which direction the wave is propagating in.

Suppose that in our cathode ray tube experiment, we know the energy of the electrons exactly because we can control the energy with which they leave the electron gun. The solution is:

This wave function is a superposition of two wave functions describing plane waves. The first, with coefficient A, is a plane wave propagating in the direction of k. The second, with coefficient B, is propagating in the opposite direction. Since in our experiment, we know that all of the electrons are propagating in the direction of +k, B must be zero. If there was something causing any electrons to reflect back towards the gun then B would not be zero. So we have:

The fact that this is a plane wave explains the wave behavior of the electron. Just as light waves are propagating disturbances in the electromagnetic field, the electron waves are propagating disturbances in a “probability amplitude field”. When those “probability waves” encounter a double slit barrier, they interfere just like light waves do.

Conclusion: Particle, wave, both, or neither?

So is it fair to say that everything in nature is both a particle and a wave? No, this isn’t quite accurate either. What’s really going on is that sometimes, it’s more efficient to explain physical processes in terms of particles, and sometimes it’s more efficient to explain physical processes in terms of waves. The modern view is that these processes are actually interactions between various quantum or classical (depending on context) fields, which are consider to be the fundamental physical entities.

Closing remarks and copyright stuff

I wrote this article essentially as a preview for an upcoming article (or possibly series of articles) about Schroedinger’s equation. The first of these should be done in the next few days, so stay tuned for that.

I have cited any pictures that are not my own original work. Fair use guidelines protect the use of this material for purposes of reporting, instruction, and criticism.