Understanding the Higgs Mechanism

If you have an elementary knowledge of physics, it is very possible that you are unsatisfied about the metaphoric explanations of the role of the Higgs boson in “giving mass to other particles”. On the other hand we do not explain gravity and electromagnetism in a similar way. We teach them using mathematical equations, whose meaning is very clear and precise, and allow for the computation of measurable quantities.

In a recent post by Ethan Siegel, he correctly pointed it out that most of the mass of the Universe comes, in fact, from strong interactions inside nucleons (protons and neutrons), i.e., the mass m of a proton is, in fact, the result of the interaction between its constituents whose energy sum up to mc².

Yet, the reason why we believe that the “Higgs boson gives mass to fundamental particles” is not so manifest. I wrote few scientific papers [1][2][3] on the subject that I am trying to summarise below. In order to continue reading, you are supposed to be familiar with the physics of electromagnetic fields.

Consider, e.g., a charged particle at rest, in a uniform electric field E. Such a field can be found, e.g., inside a parallel plate capacitor. At distance h from one of the plates, the voltage is V=Eh. V is called the potential at that point.

The energy of the particle can be computed as U’=qV. Such a quantity can be thought of as a measure of the strength of the interaction between the particle and the field. It is proportional to the coupling constant q between the particle and the field E, and is a (scalar) function of the coordinates (V=Eh). As a general rule, a potential energy is always written as U’=cP, c being a coupling constant and P a scalar function of the fields and the coordinates (the potential).

The energy stored within the volume Sd of the capacitor, S being the area of the plates and d their distance, is carried by the electric field and is u=½εE²Sd. It is worth noting that, in general, the energy carried by a field is proportional to its strength squared (e.g., the magnetic energy density stored in a solenoid is u=B²/2μ). In other words, the energy of a field is always in the form u=𝛾F², Fbeing the field, and 𝛾 is proportional to the volume in which the field is contained and to a self-coupling constant (ε or 1/μ, respectively). That can be thought of as a measure of the strength of self-interaction between fields.

Thus, the total energy in the region, inside the capacitor, becomes U=U’+u=qV+½εE²Sd.

According to Albert Einstein, we should include the energy at rest of the charged particle, whose mass is m, such that U becomes U=qV+½εE²Sd+mc². Where the latter term comes from? It is not in the form cP, nor in the form 𝛾F²!

Ok, let’s get rid of this term and let’s suppose that there is another field W’, whose potential is H’, in that region, with which the particle interacts, too, with a coupling constant g. We should thus write the total energy as U=cP+½εE²Sd+gH’+½⍺W’²Sd (The factor ½ in the latter term has been introduced to make the similarity between the terms manifest).

Suppose also that, in contrast with E or B, the W’ field permeates the whole universe, such that its minimum possible value is not zero, but W₀, so that W’=W₀+W. Correspondingly H’=H₀+H. The extra field adds an energy to the system is equal to

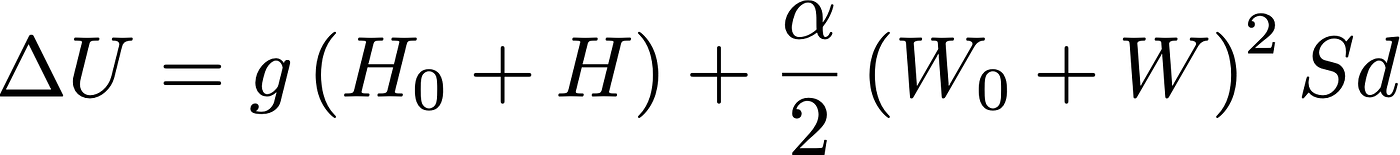
and, removing the parentheses and expanding the square, we find,

The first term in the sum is a constant that depends on the coupling between the particle and the field H₀. The coupling will be different from particle to particle. If mc²=gH₀, the origin of the energy at rest is clear: it is a measure of the strength of the interaction of a (massless) particle with the minimum Higgs field H₀ present in every point of the Universe.

It is worth noting that all other terms can be interpreted such that they, in fact, represent the foreseen behaviour of a Higgs field in the standard model: there is an interaction between Higgs bosons and matter particles, a mass term for the field (the Higgs boson mass) and a self-coupling of the Higgs field. If you want to know more about that, you can read one of the papers in the bibliography, below.

The model makes it clear how the strong interactions inside a nucleon gives rise to a mass term. The mechanism is the same: the strong field (represented, in quantum mechanics, by gluons) interacts with quarks in a very small volume, such that the interaction energy is βG’=β(G₀+G). The “constant” (it depends on the interacting particles) term βG₀, appears to us as mc², m being the mass of the nucleon (a proton or a neutron).

¹ G. Organtini, ”Unveiling the Higgs mechanism to students”, Eur. J. Phys. 33 (2012) 1397–1406 (arXiv:1207.2146v2)
² G. Organtini, “An introduction to the Higgs mechanism based on classical physics secondary school curriculum”, PoS EPS-HEP2017 (2017) 563.
³ G. Organtini, “The Higgs mechanism for undergraduate students”, Nuclear and Particle Physics Proceedings 273–275:2572–2574