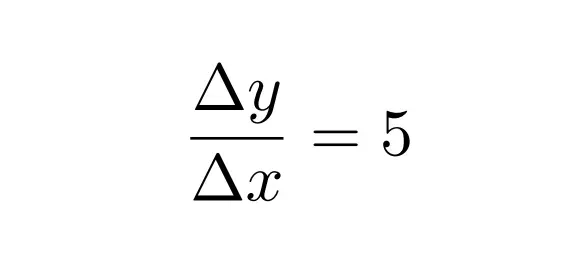
When two lines are perpendicular (or orthogonal) with each other, it means they form a 90° angle when they intersect. If you were taught about perpendicular lines in Algebra or for the SAT, you were probably forced to memorize something like “the slope of the perpendicular line is the negative reciprocal slope of the original line.” I want to focus on why this is true and expand on how we can use calculus to generalize these ideas to functions that are not lines.

For the purposes of this article, let the blue line be the original line, and the pink line be the perpendicular.

Currently, the only thing we know about the pink line is that it forms a 90° angle with the blue line.

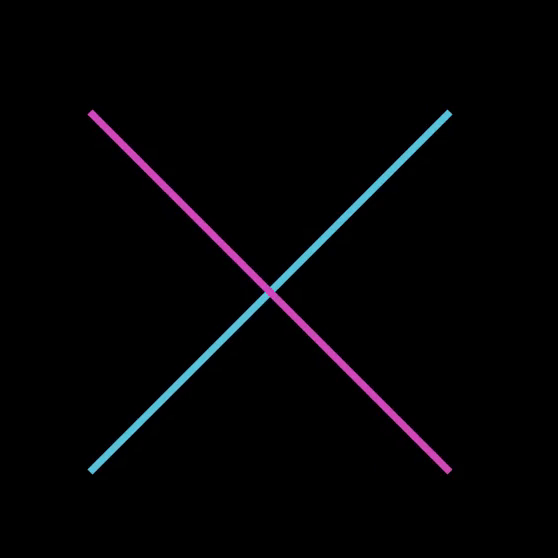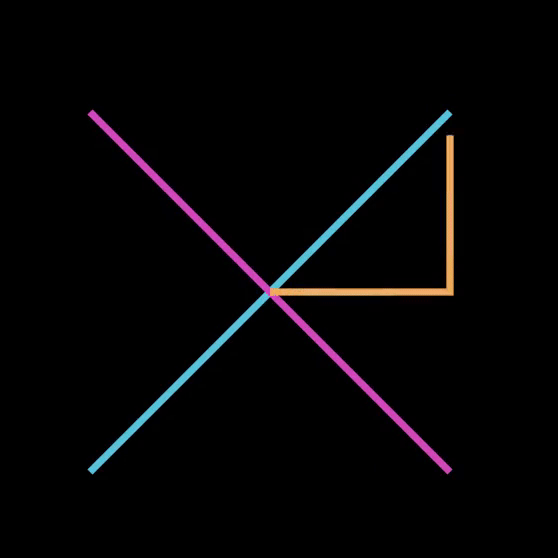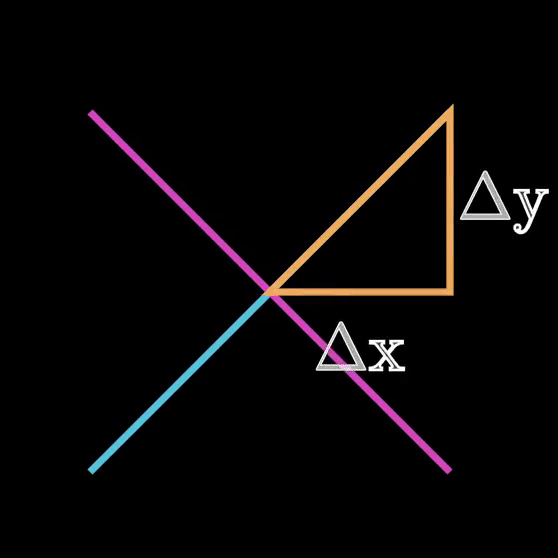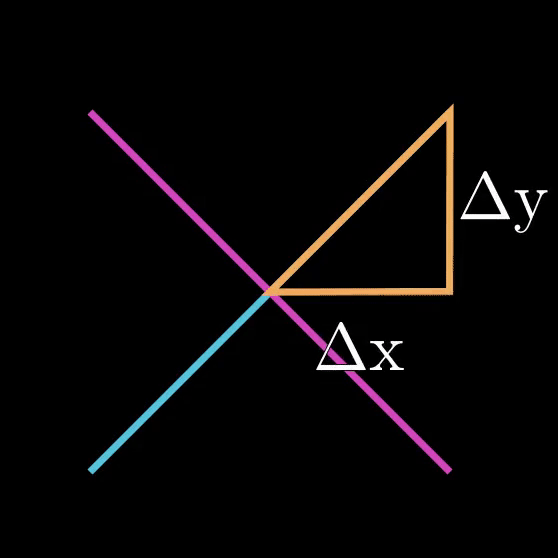
First, we have to define the slope of the blue line. So we can start by drawing a right triangle and label the sides: Δy and Δx.

At this point, we need to somehow leverage Δy and Δx, to express the slope of the pink line.

Take a crack at it before going any further. (HINT: Use the geometrical properties of perpendicular lines)

According to the animation, the triangle is reflected twice to get the slope of the pink line. First, the triangle is reflected across the blue line, and then reflected across a vertical line in the middle.

After the second reflection, the triangle is adjacent to the pink line. This gives us the ability to find the slope of the pink line.

Hence, we can conclude the magnitude of the pink line’s slope is Δx/Δy of the blue line. But, what about the direction?

If you take a closer look at the last animation, we can see the triangle and line both pointing in the downhill direction, which means we will have to multiply by a factor of -1 to account for direction. Therefore, the actual slope of the pink line is -Δx/Δy of the blue line. Let us try an example:

If the slope of the blue line is 5, what is the slope of the pink line?

We can start the problem by writing an equation for the slope of the blue line.

Now to account for the pink line, we replace Δy/Δx with -Δx/Δy (the negative reciprocal).

Finally, we solve for Δy/Δx to get-

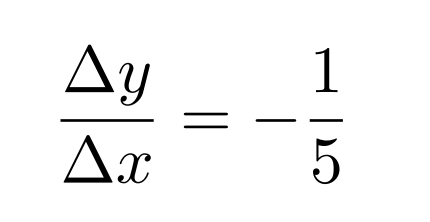
Hence, when the slope of the blue line is 5, the slope of the pink line is -1/5.

This process might seem tedious right now, but will be invaluable once we start talking about calculus.

Now, what if we wanted the perpendicular function of a non-linear function?

Orthogonal Trajectories

The only problem that arises with the previous approach is that non-linear functions have curves and changing slopes. To fight this, we need to shift from a macro perspective to a micro perspective.

When any smooth continuous graph is looked at through a magnifying glass, it looks approximately linear. If we were going to use calculus jargon to say this, we would call graphs that looked this way “local linear”.

This means we can use the “Δx and Δy approach”, but this time we need to upgrade to dx and dy because the triangle sides are infinitesimally small.

Let us see how this can be applied by trying to find the orthogonal function of y=x².

First, we start off by taking the derivative of y = x².

Now, we have to replace dy/dx with -dx/dy, to mimic the “Δx and Δy approach” taken in the first example.

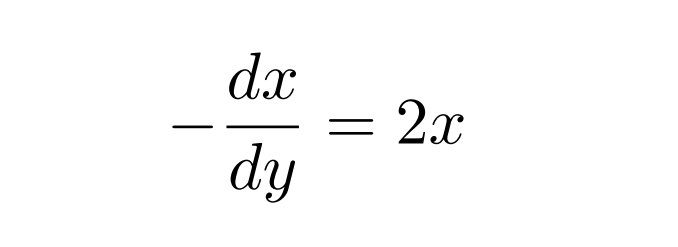
Then, to solve this equation, we separate the variables and integrate:

Which further simplifies to:

In the final solution, k is a constant, which is determined by the initial conditions. We can test this out by graphing the function:

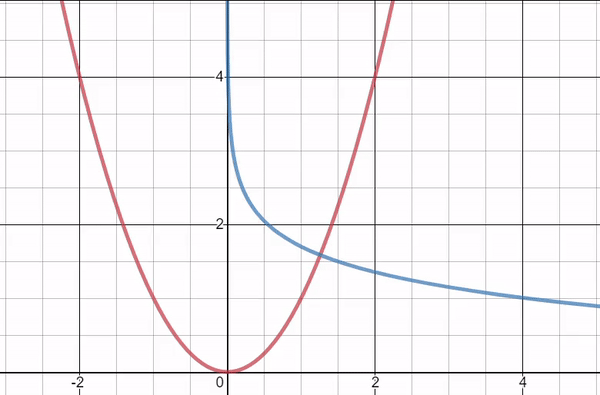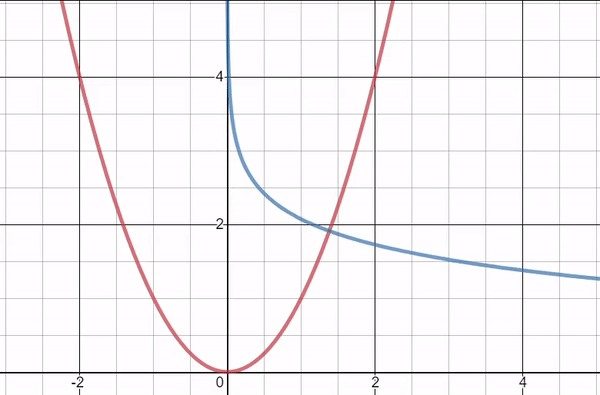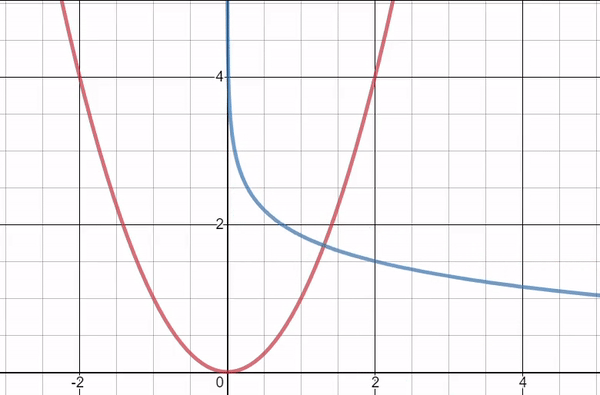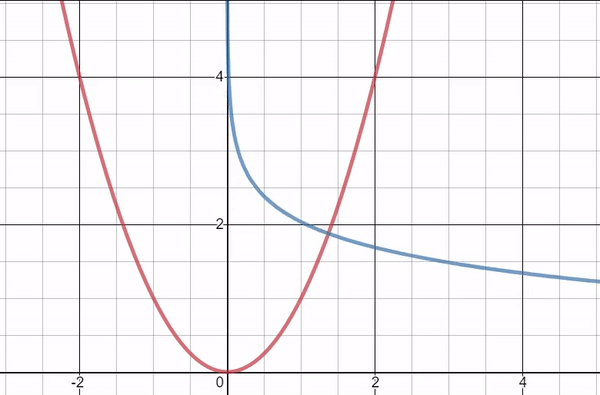
In this graph, the red curve represents y = x² and the blue curve represents the orthogonal trajectory, which we just derived.

As the point of intersection changes, k changes, but the blue curve is always perpendicular to the red curve at the point of intersection.

Conclusion

While perpendicular lines are a basic concept, orthogonal trajectories are an extremely important concept used frequently in many fields. For example, in physics, when dealing with electricity, the electric field is always perpendicular to the equipotential lines. So, it is common to have either an equation for the electric field or equipotential, and be expected to come up with the other.