Two Myths of Numerical Integration, Debunked

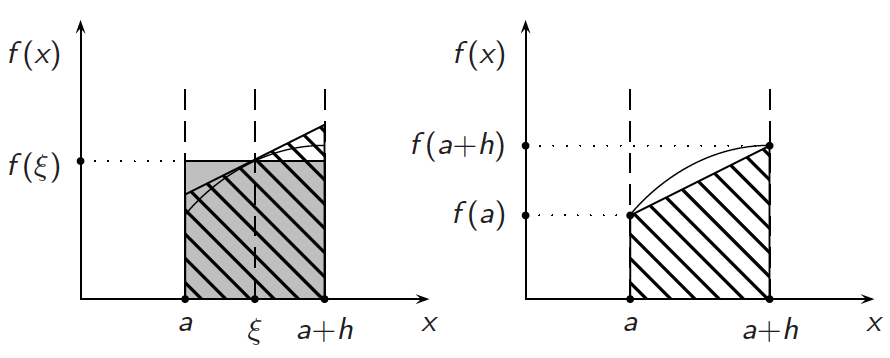
Many programmers believe that the use of higher order integration algorithms, combined with a large number of integration interval divisions, is useful (and sometimes necessary) to achieve good accuracy. In this article we show that this is not always true.

Myth No. 1: Higher Order Methods Are Better

Browsing Cantor’s Paradise articles, one of my favourite publications on Medium, I found an article written by Kazi Abu Rousan, in which the use of the trapezoidal rule for numerical integration is advocated (I am attracted by articles about physics, numerical methods and programming, as well as about the interplay between art and science). It is a well written article, in fact (as usual, on this publication) and I appreciate very much the animated figures that clearly illustrate the method. Bravo!

Indeed, the article is correct in every detail, yet the conclusion to which it may lead may not be such. Let me start with the example provided in the Kazi’s article. Here the integral of 1/(1+x²) is computed within 0 and 1, finding the number n of steps in which the interval must be divided until the precision is of the order of 10⁻⁶. In the original example, n is increased by 15 each iteration; I just modified the program such that n is increased by 1. Moreover, I stop iterating when the remainder (i.e., the difference between the actual value of the integral and its numerical estimation) is below the given tolerance. Using the trapezoidal rule, I obtain the given precision dividing the [0,1] interval in n=204 parts. Using the rectangles rule, described in Kazi’s article, too, the number of divisions needed to achieve the given precision is n=145. What? Wait…how can dividing the interval in less sub-intervals, and, moreover, using a lower order integration rule, lead to a result consistent with a higher order method with more iterations?

For your convenience, I show the integration algorithm, as I modified it, below.

original_value = np.pi/4def rectangles(f, a, b, tol):
sum = 0
n = 1
dx = (b - a)/n
while abs(sum - original_value) > tol:
sum = 0
dx = (b - a)/n
x = a + 0.5*dx
for i in range(0, n):
sum += f(x)
x += dx
sum *= dx
n += 1
return sum, n-1

In fact, there is a trick. The trick consists of the fact that I used a special version of the rectangle rule, known as the midpoint rule. In this case, the height of the rectangle, used to approximate the function, is not f(a), nor f(b), but f((a+b)/2). You will have no difficulty in showing that the area of a rectangle whose height is the average of the lengths of the bases of a trapezoid is equivalent to the area of the latter. The two methods are, in fact, completely equivalent. The difference in n is mainly due to the specific properties of f(x) (in particular, to the fact that f(x)is monotonically decreasing).

Indeed, the midpoint rule is a special case of the so-called Gaussian integration methods, which exploit the symmetries and other properties of the function to be integrated, to make a clever choice of the points in which f(x)=P(x,m), P(x,m)being a polynomial of degree m.

Myth No. 2: Good Accuracy Implies Large n

It can be shown that the remainder of a numerical integration algorithm, defined as the difference between the approximated and true values of an integral, can be written as

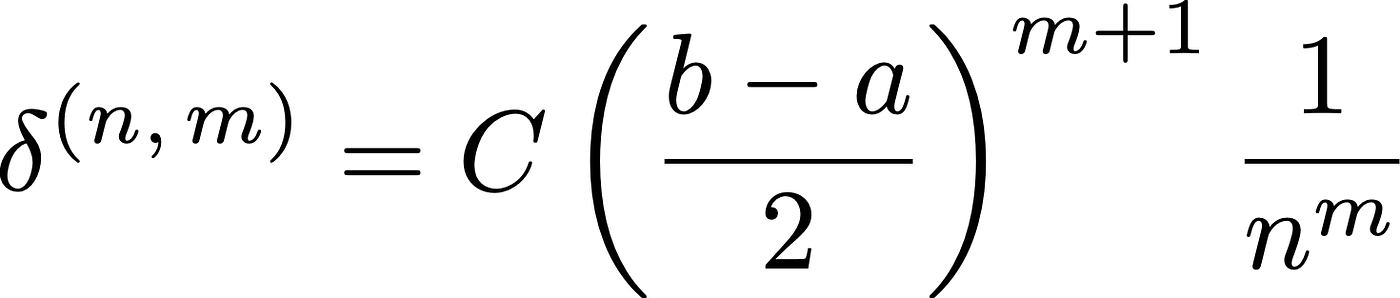
where C is a constant that depends on the m-th derivative of f(x), m is the degree of the polynomial used to interpolate f(x) and n the number of intervals in which [a,b] is divided. For the rectangle rule, m=1, while m=2 for the trapezoidal and for the midpoint methods (that, as shown above, is equivalent to the trapezoidal rule). A formal demonstration could be boring, but it is easy to understand that the larger the interval [a, b], the larger the error, so 𝛿 increases with b-a and decreases with n; moreover, how fast the error increases or decreases depends on the degree m of the polynomial used to approximate f(x).

To achieve the given tolerance just below 10⁻⁶, we needed n≃145 in the most favourable case. Below, I show you how the numerical integral I(n) evolves with n, when estimated using the midpoint method for which the “effective m” is m=2.

The remainder tends to zero as 1/n² when n tends to infinity. Thus, if we plot I(n)as a function of 1/n², according to the above formula, we should expect I(n) to follow a linear behaviour. Indeed, here is how I(n) evolves as a function of 1/n²:

Thus, in order to achieve the same precision, it is enough to compute the same integral numerically for n=3, 5, 7 and 9, then fit the data against a straight line: its intercept coincides with the estimation of the integral for n=∞. The remainder, in this case, is 1.5⨉10⁻⁷, one order of magnitude better than the one obtained with n=145!

The fit can be done using the following code:

from scipy import optimize
p, cov = optimize.curve_fit(line, xx, Integration_values)

where xx is a list of 1/n² values and Integration_values is the corresponding list of integral estimations. line is a function defined as

def line(x, a, b):
return a * x + b

The integral will thus be given by p[1]. Its remainder can be statistically estimated as the square root of the corresponding element of the covariance matrix cov[1][1], as

print("I: {:.2e}+-{:.2e}".format(params[1], np.sqrt(cov[1][1])))

Running our example above we got

I: 7.85e-01+-6.93e-08

In the end, evaluating f(x) just N=3+5+7+9=24 times, we obtained a better precision with respect to the case n=145, which requires to evaluate f(x) 145 times. Not bad, isn’t it?

Of course, the apparent saving of a factor 145/24≃6 in computing time is, at least partially, lost because of the need to fit the data. However, a straight line fit is, in fact, straightforward, and can be achieved with a very simple algorithm, such that the time spent in doing it is negligible. In fact, while we needed 0.0066 s to compute the integral using the midpoint rule and n=145, the time needed to compute it with a precision better than an order of magnitude was, in fact, 0.0012 s.