This subject is one of the most intriguing and mind-blowing in all of mathematics. A lot of ground is uncovered in this area and despite intensive research, we have still a lot to learn and a long way to go.

Let’s warm up by thinking about the number line.

The Number Line

The numbers as we normally think of them, that is, as a number line stretching from negative infinity to positive infinity with 0 right smack in the middle and a lot of famous numbers in between like e, π, etc. are called the real numbers and the set of real numbers is denoted by ℝ.

The set contains many well-studied subsets of numbers including the natural numbers ℕ = {1, 2, 3, …}, the whole numbers ℤ = {…-2, -1, 0, 1, 2, …}, and the rational numbers which are numbers that can all be expressed as a fraction of two whole numbers. This set is denoted by ℚ.

Before moving on, let’s introduce some notation. That a set of numbers say 𝔸 is contained in another set of numbers say 𝔹 is written as 𝔸 ⊂ 𝔹. In this notation, we have

ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ.

which are natural, whole, rational, real, and complex numbers respectively. Note that a whole number can always be written as a fraction, so all whole numbers are rational.

About 500 B.C., there was a community (closer to a cult in our day's terms) called the Pythagoreans and they believed that all numbers were rational numbers. But then one of their own philosophers, Hippasus proves that the square root of 2 is not rational.

The proof is brilliant and simple and is one of the pearls of mathematics and the stars of the history of mathematics for sure. The Pythagoreans were so outraged by Hippasus’ proof that they drowned him.

To be clear, Hippasus proved that

This proof implies that there exist numbers that cannot be expressed as a fraction of whole numbers. We call these numbers irrational numbers.

The set of irrational numbers is a subset of the real numbers and amongst them are many of the stars of mathematics like square roots of natural numbers, π, ζ(3), and the golden ratio ϕ.

This divides the real numbers into two non-intersecting sets. The rational and irrational numbers.

Of course, there are infinitely many irrational numbers and infinitely many rational numbers but for a mathematician, saying that a set is infinite is simply not good enough. Because of Georg Cantor’s investigations into the theory of cardinality (or infinities), we know that sets come in different infinities and it turns out that the set of irrational numbers is not just “bigger” than the set of rational numbers, it is a different and bigger kind of infinity.

Transcendental Numbers

It turns out that some of the irrational numbers come from roots of polynomials with whole-number coefficients.

For example, the square root of 2 is a root in the polynomial f(x) = x² -2.

Such numbers are called algebraic numbers. And they include all the rationals because any fraction is a root of a linear polynomial on the form ax+b. Complex numbers can also be algebraic e.g. the imaginary unit is algebraic because it is a root of the polynomial x² +1.

Many of the famous irrational numbers are algebraic as e.g. the golden ratio ϕ since ϕ is a root in the following polynomial

x² − x − 1.

A real number that is not algebraic is called transcendental.

Since they are non-intersecting i.e. you cannot both be algebraic and transcendental, the real line can be partitioned into two non-intersecting subsets, the algebraic numbers, and the transcendental numbers.

Transcendental numbers had been conjectured to exist for a long time before anyone found one. Joseph Liouville first proved the existence of transcendental numbers in 1844, and later he even constructed such a number.

Georg Cantor proved with a simple argument that there were countably many algebraic numbers (so that the cardinality of the algebraic numbers is the same kind of infinity as the cardinality of the natural numbers) and as we know that there are uncountably many real numbers (also proved by Cantor using his famous diagonal argument), we can deduce that almost all real numbers are transcendental!

Up until the end of the 19’th century, people had only found transcendental numbers by constructing them. They hadn’t really proved that any famous and well-studied numbers were transcendental.

However, that all changed when Ferdinand von Lindemann proved something remarkable.

He showed the following:

It’s hard to fully appreciate and grasp the usefulness and beauty of this theorem. He instantly found infinitely many transcendental numbers many of which were well-known to us and some of which we had been studying for thousands of years but the transcendentalness of these seemed far away.

Sometimes the contrapositive version of the theorem is useful. It states:

The Most Famous Equation in Mathematics

Of course, Lindemann knew of Euler’s Identity which has been called the most beautiful equation in the world. It states the following.

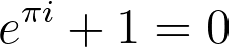
By the contrapositive version of Lindemann’s theorem, we now get that πi is transcendental, but since i is algebraic, π must be transcendental.

This follows from the fact that algebraic numbers are closed with respect to multiplication i.e. if a and b are two algebraic numbers then ab is algebraic. This is not completely obvious but one can use symmetric polynomials and some cleverness to show this.

After this, π has been proven transcendental many more times in different proofs.

Future Challenges

We don’t really know much about transcendental numbers and we don’t have many useful tools that we can use to prove that certain candidates are transcendental.

We don’t even know if eπ or e + π is transcendental. We also don’t know if the Euler-Mascheroni constant γ is transcendental — we don’t even know if the Euler-Mascheroni constant is irrational!

It is a catastrophe and quite embarrassing that we know so little about such an important number.

And in general, we know of very few transcendental numbers, especially taking into account how many there are. Even if we know that a number is irrational, in general, it doesn’t help us much towards proving that it is transcendental.

If you prove a number to be transcendental, that wasn’t known to be before, you will be very famous.

In mathematics the art of asking questions is more valuable than solving problems

~ Georg Cantor