I love these three math problems! The first one requires very little math skill — but it is maybe the most difficult one. The second one only requires basic geometry. For the third one, you need to know elementary algebra.

Three Problems

Problem 1: The 316 problem

I call this problem “the 316 problem” because 316 is not a solution, but almost! The problem is :

The 316 problem

Find an integer number such that it gets exactly twice as big if you move the last digit first.

Take 316 for example: If you move the last digit first, you get 631. If you double it, you get 632. Close, but not equal. We want a normal decimal number.

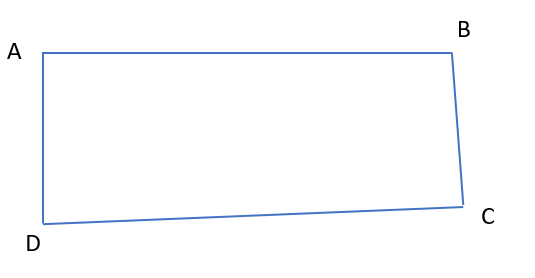
Problem 2: 90 degrees equals 100 degrees

Step A. Draw four lines as the figure below shows. The angle DAB is 90 degrees. The length of AD is 5 cm. The angle ABC is 100 degrees. The length of BC is also 5 cm.

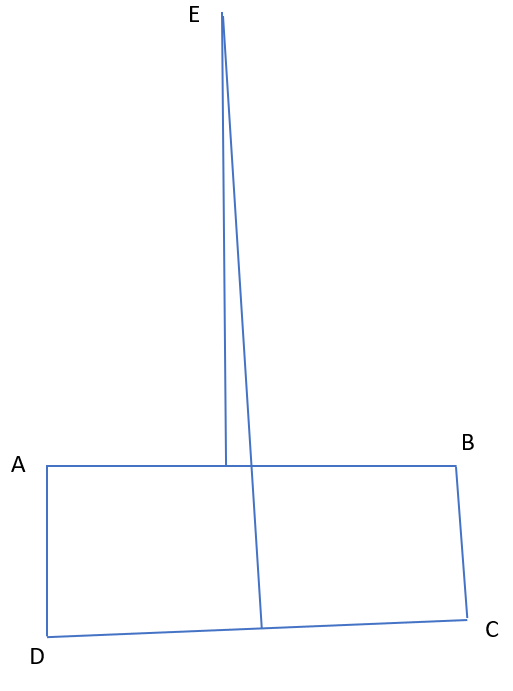
Step B: Draw a line perpendicular to AB, at the exact middle of AB (a perpendicular bisector). Do the same to CD. Since AB and CD are not parallel, the two new lines will not be parallel either. Call the intersection point E.

Step C: Draw lines from E to all four corners of the original figure.

Step D: Let us examine the two triangles △ EAD (red) and △EBC (green).

1. Sides EA and EB have the same length since E is on the bisector to AB.
2. Sides ED and EC have the same length since E is on the bisector to DC
3. Sides AD and BC have the same length since they are both 5 cm long.

Hence the two triangles are congruent and their angles are the same.

In particular, angle DAE equals angle EBC. But angles EAB and EBA are also equal since E is on the bisector to AB. Now subtract the smaller angles from the larger angles. The remainder is angle DAB, which is 90 degrees and angle ABC, which is 100 degrees. Which proves that 90 degrees is equal to 100 degrees.

What is wrong with this geometrical proof that 90 degrees equals 100 degrees?

Problem 3: Imaginary power

The imaginary unit i is defined by its property i² = −1. Most people, including me, find it hard to imagine a number which multiplied by itself becomes -1!

A real number raised to itself is not so hard to understand, like 3³ which is 27. But i raised to itself? If i is hard to imagine, i raised to i must be completely unthinkable.

No, it is 0.21! Can you prove that?

Three Solutions

Solution 1: The 316 problem

Let the digits of the solution be represented by letters a b c … x y z (not implying that the solution necessarily has 26 digits). We can then write the following addition:

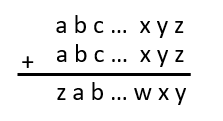
What is the last digit, z? We can only guess. Is there any reason why it wouldn’t be 3? Let’s try that:

We can now see that if z is 3, y must be 6:

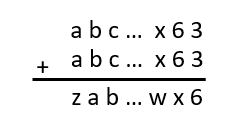
And we now can see that if y is 6, x must be 2!

Then w must be 5. And so on. Now we just carry on until we have a solution:

The last digit being 3 — was that just a lucky guess? No, anything goes, except 0 and 1. I made a small Excel sheet that calculates the solution when you enter the ending digit. Here are the solutions ending 2 to 9:

Solution 2: 90 degrees ≠ 100 degrees

The drawings in the illustrations are wrong. The intersection point E should be much higher up. Then the line EC will be to the right of point B, not to the left. Increase the angle ABC from 100 degrees to 135 degrees and this becomes obvious.

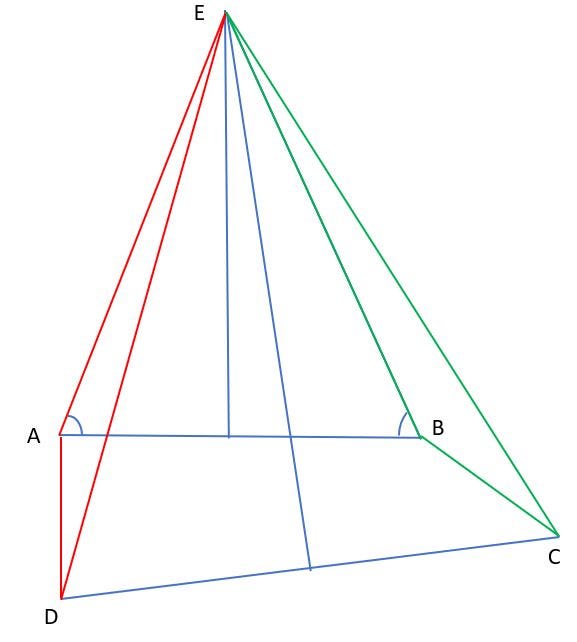
Call the angle ∠EAB α and the angle ∠ABC β. With the wrong drawing, we have α + 90 = α + β. With β = 100, this leads to the contradiction 90 = 100.

With the correct drawing, we have α + 90 = 360 - α - β. α = (270 - β)/2. With β = 100 we get α = 85, which shows that point E is much higher up, but there is no contradiction.

Solution 3: Imaginary Power

Start with the well known Euler’s identity:

Re-write it as:

Take the square root of both sides:

Raise both sides to the power of i:

For a longer discussion of this problem, see for example this reference.