Thinking Relativistically

In my last article on special relativity, I explained how and why our intuitive understanding of space and time needed to be modified to account for developments in electromagnetic theory that took place in the 19th century, in particular the results of the Michelson-Morley experiment and the non-covariance of the electromagnetic wave equation under the Galilean transform. I explained how length contraction, time dilation, the invariance of the spacetime interval, and ultimately the Lorentz transformation follow from the two postulates of special relativity:

• First postulate: The laws of physics take the same form in all inertial reference frames.
• Second postulate: The speed of light has the same numerical value in all inertial reference frames.

Having seen that we live in a relativistic universe, it’s now time to look at the ways in which our thinking must be adjusted in order to properly understand physics in a relativistic universe.

Reference frames

Special relativity is ultimately a theory about the ways in which the same physical phenomena will appear to observers in different reference frames. All of the important and famous ideas that are associated with special relativity, like mass-energy equivalence, the impossibility of time travel, the speed of light as the universal speed limit, and the phenomenon of red shift all follow from those assumptions.

To mathematically express the law of motion for a physical system and to measure the parameters of that system, we need a coordinate system. However, coordinate systems are mathematical abstractions and Nature does not a priorirequire that coordinate systems must exist or that any particular coordinate system must be used for describing a physical system. To use a coordinate system, we will need to declare one. To do so, we will first declare a reference, which consists of a point at some location in physical space and a system of perpendicular lines intersecting at that point. We can then use the reference to declare a Cartesian coordinate system by saying that the reference lines are the axes and the origin is their point of intersection. The combination of the coordinate system and the reference is called the reference frame.

The choice of the location of the origin and the orientation of the axes will always be in reference to a physical object or collection of objects, such as the position of a person standing on a train with the x-axis pointing towards the front of the train or the center of a cube with the axes perpendicular to the faces of the cube. Nothing prevents us from defining multiple reference frames for the same system. For example, we might also define a reference frame attached to the position of a person standing by the tracks watching the train go by, or we might define a reference frame fixed at the position of somebody who’s watching the cube rotate. In this case, the reference frames are in motion with respect to each other.

This is is why it’s important to not confuse the coordinate system with the entire reference frame. A coordinate system is ultimately a function that maps points in space into ordered tuples of numbers and it is nonsensical to say that a function, which is an abstract mathematical object, is rotating or moving in physical space. For our purposes, this function will be defined in terms of the reference. For example, the two-dimensional Cartesian coordinate system will send a point P to the ordered pair F(P)=(x(P),y(P)) where x(P) is the perpendicular distance from point P to the y-axis and y(P) is the perpendicular distance from point P to the x-axis:

In this case, F(P)=(2,3), so (2,3) is the coordinate pair of point P.

We will only consider inertial reference frames, meaning frames that are moving at constant velocity with respect to each other and not accelerating or rotating. Special relativity can account for non-inertial frames as long as gravity isn’t what’s driving the acceleration (for that you need general relativity) but we will hold off on this until much later in this series. The reason for this is that if it was possible to detect absolute velocity then it would be possible to define an absolute reference frame and this would contradict the fact that Nature does not a priori come equipped with a coordinate system. However, absolute accelerations are detectable because accelerations imply forces and a force either acts or does not. If this was not the case then it would be possible for a physical process to be occurring in one frame but not in another, which violates the first postulate.

We will usually be interested in situations where an experimenter is observing the motion of some physical object, and neither the observer nor the object are subject to any acceleration. The unique frame where the object’s velocity is zero is called the rest frame (or proper frame) S′ and the unique frame where the observer’s velocity is zero is called the observer frame (or lab frame) S. It will usually be obvious which is which. Finally, we will always assume that the observer and rest frame are in standard configuration, meaning that S′ has constant velocity in the x-direction with respect to S, the origins of their coordinate systems coincide at t=t′=0, and the coordinate axes in both frames are parallel:

The coordinates in the rest frame are labelled with primes, (t′,x′,y′,z′) and the observer frame coordinates are labelled simply (t,x,y,z) and these coordinates are related by the Lorentz transform:

We will almost always ignore the y and z coordinates.

The symbol γ denotes the Lorentz factor:

One last point before we move on. If an object is determined to have length L in frame S and length L′ in frame S′, if the time interval between two events is Δt in frame S and Δt′ in frame S′, or if the speed of a particle is U in frame S and U′ in frame S′, then I do not say that L, Δt, and U “appear” to have different values in different frames. The word “appear” implies that the difference in these values between frames is somehow an error or an illusion that causes them to deviate from a single “true” value or that the frame dependence of these quantities represents a limitation of our knowledge. This is not the case. There is no such thing as the true length of an object, the true time interval between events, or the true speed of a particle because measuring these things requires a coordinate system and therefore requires a reference frame. There is no single “correct” reference frame, so there is no single “correct” value of these quantities.

Now let’s get to the heart of the matter and use what special relativity tells us about reference frames to analyze some physical problems.

Invariance of causality and the relativistic speed limit

Observing a physical system from a different reference frame doesn’t add anything to the physics that underlie the behavior of that system. This means that anything that is true in one frame must be true in every other frame, although the explanation for why that thing is true may change. Put another way, changing your frame of reference does not change the facts of Nature, and one of the most important facts of Nature is the causal relationships between physical events. If event A causes event B in one frame then there is no frame in which event B causes event A. This is called invariance of causality. We can use invariance of causality to understand what it means when we say that c is the “universal speed limit”.

Suppose that there is a frame S in which event A causes event B via propagation of a faster-than-light signal, for example, by firing a bullet with speed U>c. In this frame, let Δx be the distance between the two events and let Δt be the time separation between them so that U=Δx/Δt. Since event A precedes event B in frame S, Δt must be positive. Let S′ be a frame moving with speed v<c relative to S. Then by the Lorentz transform:

If c²/U<v<c, which must be allowed because all speeds less than c are allowed, then we have found a reference frame in which Δt′ is negative, which means that in this frame B will precede A, and this is not allowed.

What this means is that if one event causes another event then it must do so by propagation of a signal travelling no faster than the speed of light. This is often stated as “Information cannot travel faster than light”. However, we’ll see in a later section that a signal can travel from event A to event B at a speed faster than c if that signal doesn’t allow event A to cause event B.

Relativity of simultaneity: The relativistic snake

A very fast snake has escaped from its cage in the biology department and is rushing across a table at a speed of 0.6c. The snake’s proper length (its length as measured in its rest frame) is exactly one meter. A student intends to catch the snake with a rectangular net, which is exactly one meter wide, by slamming the net down on the table at just the right moment so that the left rim of the net will hit the table just behind the snake’s tail and the right rim of the net will hit the table in front of the snake’s head. If the rim hits the snake’s body then the snake will be harmed and the student will get an earful from her advisor.

The student’s argument is: “In my rest frame, the snake has a velocity of 0.6c so I calculate that the snake’s length is contracted to 80 centimeters, meaning that the left rim of the net will land just behind the snake’s tail and the right rim will land 20 centimeters in front of its head, and I will catch the snake without harming it”.

The snake’s response is: “I am 100 centimeters long, and the net is approaching me with a speed of 0.6c, so its width is contracted to 80cm. If the left rim of the net hits the table right behind my tail then the right rim will hit me and break my back, and you will get in so much trouble!”

The snake will either be harmed or not, so either the snake or the student is wrong. How do we resolve this paradox?

Let S be the rest frame of the student and let S′ be the rest frame of the snake. In S, let x=0 be the point where the left edge of the net strikes the table at time t=0, which coincides with the exact moment that the snake’s tail passes x=0. In S′, the frame where the snake is at rest, let x′=0 be the position of the snake’s tail. Let t₀ and t₁ be the times when the left and right edges hit the table in S and let x₀ and x₁ be the positions where the edges hit the table.

Then t₀=t₁=0s, x₀=0cm, and x₁=100cm. For v=0.6c, γ=1.25. By the Lorentz transform:

So the snake is wrong. In the snake’s rest frame, the right edge of the net hits the table 2.5 nanoseconds before the left edge. It is true that the edges of the net are only 80 centimeters apart in the snake’s rest frame, but because the edges do not fall at the same time in the snake’s frame, the points where they hit the table are 125 centimeters apart.

Here is what the snake actually sees. The two edges are 80cm apart and approaching the snake with a speed of 0.6c. The right edge hits the table at t′=-2.5ns at a position 125cm in front of the snake’s tail, or 25cm in front of the snake’s head. At this time, the left edge is still above the snake at a point 45cm in front of the snake’s tail. At t′=0s, after 2.5 nanoseconds elapse, the left edge will have traveled 0.6c*2.5ns=45cm in the direction towards the snake’s tail, and at this time the left edge hits the table just behind the snake’s tail. Neither edge hits the snake.

The snake is wrong because it neglected to consider relativity of simultaneity: two events A and B that occur at the same time but at different locations in one reference frame will not occur at the same time in any other reference frame. Furthermore, there will be frames where A precedes B and frames where B precedes A. This does not violate invariance of causality because neither of the two events causes the other, since if A and B happen at the same time but at different locations and A were to cause B then this would require a signal to travel at infinite speed from the location of A to the location of B, which is not possible.

You might have noticed a small problem: the right edge of the net continues to approach the snake at a speed of 0.6c after hitting the table. Since the right edge hits the table only 25cm in front of the snake, if the snake stops when its head reaches the right edge then the left edge will still hit the snake 20cm in front of its tail. Does this wreck our entire argument?

No. Suppose that the snake’s head stops at the moment that it reaches the right edge. This will occur at about t′=-1.39ns. Even if we assume that the snake is completely rigid, the tail will not stop at this time because the stopping of the snake’s head is causally connected to the stopping of the snake’s tail and therefore the snake’s tail cannot stop before a signal (a nerve impulse, an elastic shock wave, etc), traveling no faster than the speed of light, propagates from the head to the tail. It is not possible for the entire length of the snake to stop at the same time if the snake stops because of an event that occurs at only a single point along its length. The snake’s length in this frame is one meter and the time it takes for a signal to travel a one meter distance at light speed is about 3.33 nanoseconds, so the snake’s tail keeps moving for plenty of time to avoid being hit by the left edge of the net.

The twin paradox

Consider two identical twin astronauts. The first astronaut, A, remains on Earth and the second, B, is assigned to a mission to Alpha Centauri, about five light years away. B’s spaceship departs from Earth and quickly accelerates to 0.9c (as measured from Earth), and when B reaches Alpha Centauri she stops, turns around, and accelerates back to 0.9c to return to Earth. The acceleration is assumed to be very quick so that B spends nearly the entire trip at constant speed. A will observe the entire round trip to take nine years, but in B’s frame the distance between Earth and Alpha Centauri is contracted by a factor of 2, she sees Alpha Centauri approach her at a speed of 0.9c, and in the return trip she sees Earth approach her at 0.9c, and for her the entire round trip takes only 4.5 years and when she returns to Earth she will be 4.5 years younger than her twin.

This seems to be in contradiction with our claim that there are no preferred reference frames: why was time only dilated for B? Could B not just as well claim that she remained stationary while Earth receded from her and then returned at 0.9c?

The answer is no, because B experienced an acceleration and A did not. She started out in the same rest frame as A, but then she accelerated into a different rest frame, and then had to decelerate back into A’s rest frame. Unlike velocity, acceleration is absolute, and we can definitively say that A did not accelerate away from B.

The faster-than-light laser dot paradox

Here’s another famous one.

Suppose that an astronomer standing on the Earth shines a very powerful laser at the Moon, powerful enough to produce a visible dot on the Lunar surface. The laser is scanned across the Moon’s equator, a distance of 3,393 miles (taking into account the curvature of the surface), in 0.01 seconds. An observer standing on the surface of the Moon will see the dot rushing past at about 1.82c. But doesn’t special relativity say that nothing can travel faster than c? Have we found a fatal flaw in the theory?

No, we have not, because special relativity does not say that “nothing” can travel faster than light. What special relativity tells us is that one event cannot cause another event if this would require the first event to send a signal to the location of the second event at a speed greater than c. In this example, the laser dot is able to travel from point A to point B at faster-than-light speed because the appearance of the dot at point A does not cause the dot to later appear at point B. In a future article when we consider what special relativity tells us about rotating frames, we’ll be able to prove explicitly that there exists a reference frame in which the dot arrives at B before it arrives at A.

Twisting of a spinning rod

As a final demonstration, I’ll cover one of my personal favorites.

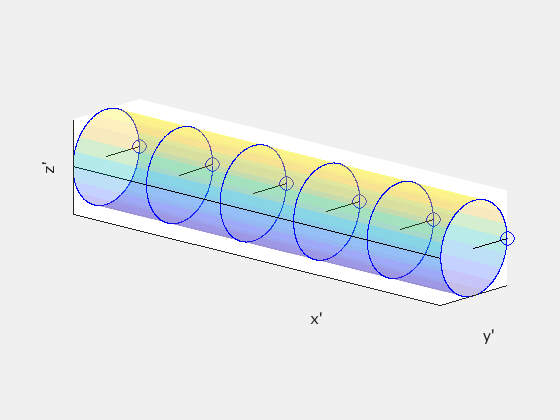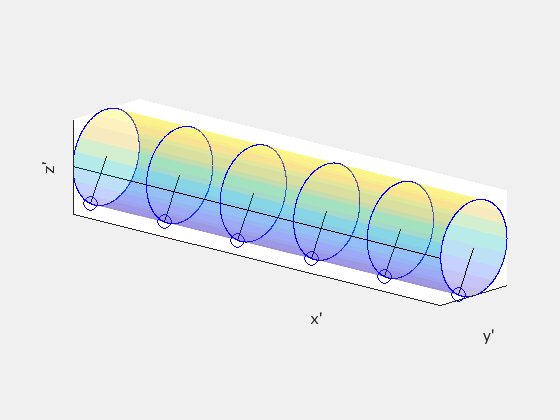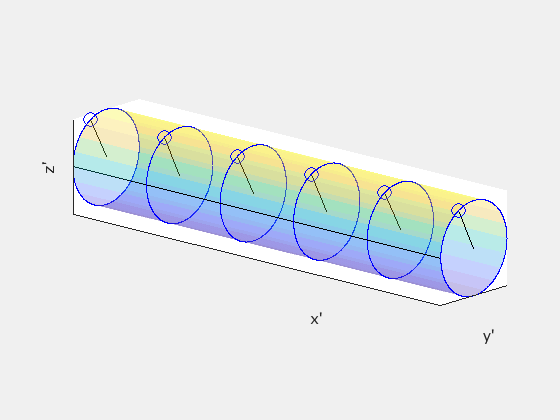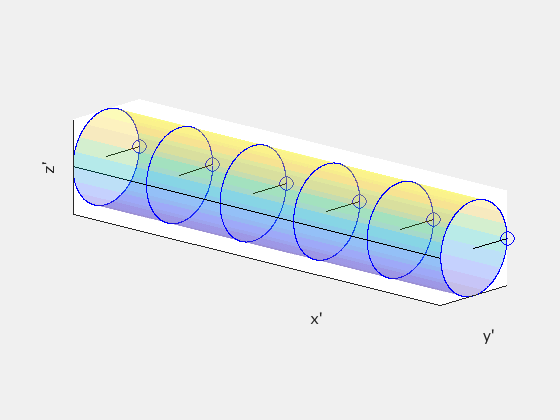
In frame S′, a straight cylindrical rod parallel to the x′-axis rotates with angular speed ω. In frame S, the rod rotates and moves forward with velocity +vx. We will see that in frame S, the rod is twisted about its length.

Start in frame S′ by dividing the rod into disks separated by unit distance Δx′=1. Treat the disks as clocks with a single “hand” drawn on each disk so that the hands are all parallel. This is what the disks should look like in S′:

In S′, neighboring hands hit the black line at exactly the same time. But because of relativity of simultaneity, this is not true in any other frame. So given Δx′=1 and Δt′=0, let’s find Δt in the observer frame S using the inverse Lorentz transformation:

This tells us that there is a time delay of γv/c² between when neighboring hands on our “clocks” will pass the black line, and since ω is the angular frequency for each hand to make one full rotation, this means that neighboring hands are offset by a phase angle of γvω/c². Note that ω takes the same value in both frames because the angular motion is happening in the plane perpendicular to the direction of the velocity of the rod. Neglecting the forward motion of the rod, this is what the clocks might look like in frame S:

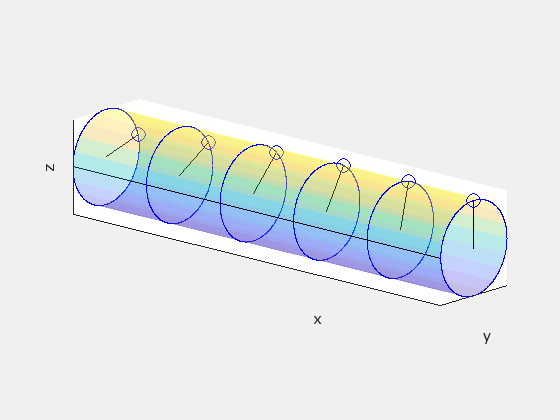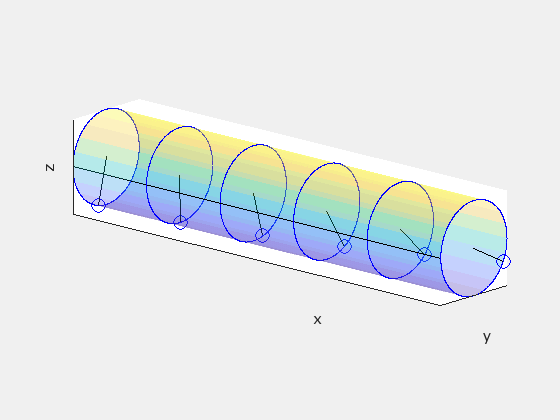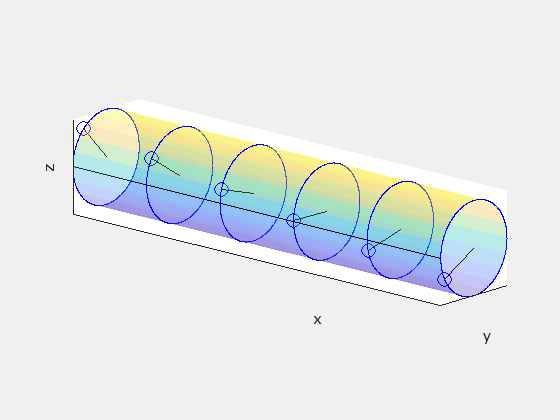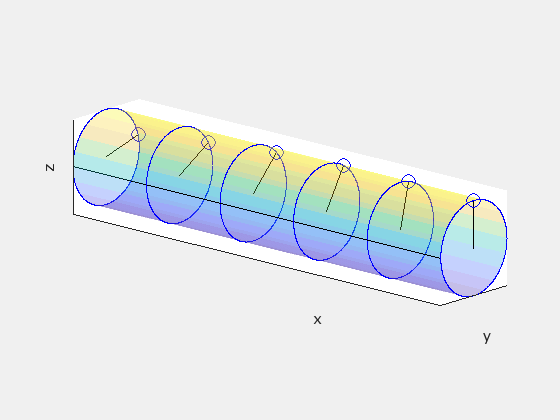
This tells us that the rod must be twisted about its axis in frame S. The following animation compares what the rod looks like in each frame, with S′ on the left and S on the right:

The rod is not being subject to any sort of twisting force or other mechanical deformation. The geometry of the rod itself is different between the two reference frames.

Conclusion

You might have noticed that, for an article about a topic in physics, we actually didn’t really talk about any physics. This was really an article about geometry: the geometry of spacetime itself in terms of how we can build coordinate systems on spacetime and transform between coordinate systems, the geometry of the behavior of moving objects defined in spacetime, and a few allusions to the geometry of causal structure. This is deliberate: relativity is a geometric theory and it is impossible to fully understand and appreciate relativistic physics without first understanding the underlying geometry. Fortunately, in the sequel to this post we will actually start to talk about some actual physics.

All images and animations in this article that have not been cited are my own original work. The use of those images that are not my own is protected under fair use guidelines.

The demonstration with the snake is a variation of an example problem that appeared in Modern Physics for Scientists and Engineers, 2nd edition, by Taylor, Zafiratos, and Dubson. The example of the twisted rod is a problem from Introduction to Special Relativity, 2nd edition, by Wolfgang Rindler.