There is no such thing as √-1

When I was at school, mathematics fascinated me. I used to spend weeks with calculating and deriving different formulas, filling notebooks and sheets of papers day and night. Complex numbers were one of my interests. But I haven’t done everything rigorously, and one day, when I showed some notes to my math teacher, she shook her head in disapproval. “This” — she’s like, pointing to some “magic” calculations with complex numbers — “is something you don’t do”. I learned that you have to have a discipline in your ideas, if you strive to reach further.

This happened a few decades ago. Today, as an engineer I keep the same fascination for math, just I have less time ;) I’ve learned how to do math better and I can share some of this knowledge here. I’ve noticed that complex numbers are not introduced in a truly understandable way in many places, and this leads to all kind of confusions. Actually, searching the Internet it is hard to find an article which introduces them rigorously or, saying in a way I could understand if I was to start them now.

For example, let’s take a video course ranked in the first 5 results in Google for “what is a complex number”. It starts with the following:

You know, there are real numbers, like 1, 2, 3.5, etc. and “i”, the imaginary number, which is √-1. A complex number is a number like a + ib …

Pardon me? Yes, I know about real numbers, they are the numbers we deal with every day. But “i”?? I have no idea what it is. Well… I know now: it is nothing else than a complex number. So “a complex number is a number in the form of a + bi, where i is a complex number” is a circular definition. What is a circular definition? “A definition that is circular”:) Do you find this satisfactory?

The “definitions” “i is the square root of −1” or “i is the number/thing with the property i² = -1” do not shed any more light here. Do they do for you?

If not, then keep reading. I promise to give you an introduction which is rigorous enough, but in the same time understandable and even enjoyable. You’ll realize that complex numbers are very simple constructions, and there is not any “magic” in them. All I ask you is to forget everything you learned about complex numbers. Well, try at least ;) And especially *i*. Remember: “There is no such thing as √-1.”

To understand complex numbers, we have to familiarize ourselves with the notion of fields. A field in mathematics is a set, along with 2 operations defined on that set: an addition operation written as a + b, and a multiplication operation written as a · b.

But what is an operation defined on a set? An operation is a mapping from a pair of objects to one result object. All 3 must belong to the same set.

As an example, let us consider the set of natural numbers, ℕ = {1, 2, 3, …}. If we take 2 objects (numbers) from the set, and add them, we’ll get an object (a result number) from the same set. E.g. 2 + 3 = 5, and 5 is a natural number too. Same story with multiplication.

These (2) operations have some properties, which sound boring at a first reading, but will be important later. We are used to commutativity, a+b = b+a, a·b = b·a. They say that the 2 elements of the operation behave the same way, no one is privileged. This is true even if there are more elements: the property is called associativity, e.g. (a+b)+c = a+(b+c). And there is one property which brings together the 2 operations, the distributivity of multiplication over addition: a · (b + c) = (a · b) + (a · c). This is important, because it allows us to do algebraic calculations the way we are used to.

Another requirement for a field operation is the existence of a special object, which, when mapped with an arbitrary element, yields the same element as a result. As an example, for multiplication this is the number 1 in the set of natural numbers, because a·1=a, for any a we take from the set. We’ll call 1 “identity object”, or IDENTITY constant.

Have you noticed something? For addition, there is no null object between natural numbers. It would be 0 (zero), because a+0=a. If we want the addition to be a field operation, we should extend our set with (the number) 0, so it becomes {0, 1, 2, 3, …}. This is the set of whole numbers, with the identity constants 0 and 1.

So far so good. But the definition of a field imposes also 2 other requirements on the set: the existence of inverses. An inverse of a set object, related to an operation is another object, which mapped with the first yields the identity (for the operation). For example, for addition, given a number a, it’s inverse is a number a’ such as a + a’ = 0.

You may have noticed here that we don’t have the additive inverse of a natural or whole number. We have to extend the set again, now with negative numbers. 2 + (-2) = 0, and the set becomes {…, -3, -2, -1, 0, 1, 2, 3, …}. These are the integer numbers.

Looking for the multiplicative inverse, a’ such as a·a’=1, we see that again, we don’t have enough objects. So we have to extend our set to rational numbers: 3 · (1/3) = 1. 1/3 is the inverse of 3.

You noticed that I put 1/3 in parenthesis above. This emphasizes the fact that it is a unique object, an entity, and not 2 objects. (1 / 3) is a rational number, represented by 2 integer numbers, separated by ‘/’. The second number must not be 0, we do not have an object in the set which would correspond to (a/0). We’ll keep our notation of rational numbers, including parenthesis in this chapter.

So far, we introduced the notion of fields, and we’ve concluded that the set of rational numbers, with the 2 operations + and · form a field. Now I’d like to show you how we can prove this in a more rigurous, mathematical way. This might sound a bit boring at first, but will help us in understanding the notions to follow. Believe me, it will pay off!

Let’s start by checking: are + and · in-set operations?

So let’s define the multiplication of rational numbers, as:

(m/n) · (m’/n’) = ((m·m’) / (n·n’)) (1)

(a bit much parenthesis, I know, but let’s keep this for now). (1) at the end is just a marker for the formula, not part of it. As you see, the result is described also as 2 numbers, separated by ‘/’. And because both m·m’ and n·n’ are integers, and n·n’ is not zero, the result is also a rational number.

Second question, still on multiplication. Is there an IDENTITY rational number, (p/q), such as (m/n)·(p/q)=(m/n) ?

1/1 seems to satisfy this brilliantly, since m·1 = m and n·1 = n.

(You are right, 2/2 will satisfy this too. We can define (m·p)/(n·p) = (m/n), no problem here.)

And we can find even the inverse of a (rational) number (m/n): it is (n/m), since (m/n)·(n/m)=(m·n)/(n·m)=1/1.

What about the addition? Well, we’ll define it as:

(m/n) + (m’/n’) = (m·n’+m’·n / n·n’) (2)

The NULL number is (0/n), and the additive inverse (-m/n). Nice, right? If you’re diligent, you can check that the distributivity of multiplication over addition holds. (You have to do this for a rigorous treatment.)

So we proved that the set of rational numbers, with its 2 basic operations defined by (1) and (2) form a field. A rational number is nothing else then a pair of numbers, (a / b), which are integers and b is not zero. If we look at it, we see that the ‘/’ character is not important here, it is just a symbol which helps gluing the 2 parts together. It could be equally something else, like ‘@’ or ‘#’, it is just a separator. A historic convention, with its own reason.

One more thing comes to mind here. If the denominator (the second number) is 1, the number behaves like an integer, and we can say a/1 = a. That means that one is able to do operations with integers, and integer numbers are a particular case of rationals, where the denominator is 1. The Q set extends the set of integers, Z.

Okay, so far so good. But what are fields good for, why have we started this journey? Well, fields — or algebraic fields, as they are known — are fundamental in several math and physics areas (e.g. linear algebra, quantum mechanics). Its properties allow us to do calculations in a similar way we used to do with real numbers.

If you followed me to this point, congratulations! I admit, some parts might sound a bit boring. But now comes the second part, which promises to be more interesting: we’re gonna build a field from scratch! This needs some creativity, so expect something exciting.

I am going to create a field who’s object I’ll call p-numbers. Because we are used to rational numbers, we’ll make an analogy. We define a p-number also as a pair of 2 numbers, a and b and we’ll write it as p = (a, b). It is similar to a rational number (m / n), just we use comma ‘,’ instead of slash ‘/’. And a and b will be real numbers in this case, not integers.

Now the operations. We are envious to the beauty and simplicity of rational multiplication ((m/n) · (m’/n’) = ((m·m’)/(n·n’)), so we are going to use it, but for addition. We’ll define:

(a, b) + (a’, b’) = (a+a’, b+b’)

Simple, isn’t it? So if I have 2 p-numbers, p = (2, 1), q = (1, 3) then p + q = (3, 4).

But this reminds me some lessons from elementary physics, where we learned that this is the addition rule of 2 vectors!

In a Cartesian coordinate system, a vector has 2 components, which are its projections on the axes. Here, vector u has components (2, 1), vector v(1, 3). If we put the tail of v to the head of u, the tip of v will be the head of w = u + v, starting from the origin. This is the so-called head-to-tail method.

Now if we move (translate) vector v parallel to itself, so as to start from origin, then obviously u+v won’t change. Note that the sum vector is represented by the diagonal of the parallelogram through their common point.

The important point for us is that we can represent our p-numbers by points, or (origin starting) vectors in the Cartesian system: p = (2, 1) by point P, vector u and q = (1, 3) by point Q or vector v. In this case, p-number r = p + q is represented by point R, or vector w = u + v. Simple, right?

Also note that (vector) u is not the same as (number) p, it is just a representationof p. Same for point P: it is also a representation. Also, the vector representation has to start from origin (in general, vectors can be translated, and keep being the same.)

Looking back at the field’s definition, we need to find the NULL object for addition, which does not alter a p-number when added to it. This is, obviously (0, 0) — represented by origin in the Cartesian coordinate system. Also, it’s easy to find the “negative” object, which, when added to p = (a, b) yields NULL: it is (-a, -b). It’s vector is the same as p, but with the opposite direction.

Before jumping to multiplication, let’s see some other properties of p-numbers. What happens with our p-numbers if the second component is 0: ex. p = (a, 0) ?

In this case the projection to the vertical axis is null, so the corresponding point will show on the x axis. The corresponding vector representations will all be horizontal and point to the right if a > 0. Also, since (a, 0) + (a’, 0) = (a + a’, 0), the sum of 2 such numbers will still stay on the x axis and will have its magnitude = a + a’. If we strip (or reset) the second component, they behave just like real numbers. So these p-numbers extend the real numbers, obtained when b = 0. You remember, just like the rationals extended the integers, got when the denominator was 1. In other words, real numbers are also p-numbers.

We’ll take advantage and call (a, 0) scalar p-numbers, or simply scalars, and write them sometimes just a, like the real number.

Now let’s define multiplication. Recall that we want to define an operation between 2 p-numbers, which yields another p-number. We’ll do this in 2 stages: first we’ll multiply with scalars.

For this, we’ll just recall how we defined multiplication in elementary school:

n·p = p + p + … { n times }

We’ll apply this definition also if p is a p-number. So, for example:

2·(a, b) = (a, b) + (a, b) = (a+a, b+b) = (2·a, 2·b)

and generally

n·(a, b) = (n·a, n·b)

where n can be not only an integer, but a real number as well. The following figure shows the vector interpretation of this definition.

In the figure, v = 2·u and w = 3·u . It’s easy to see that by a scalar multiplication, the vector will have it’s magnitude (length) multiplied, while it’s direction will stay unchanged.

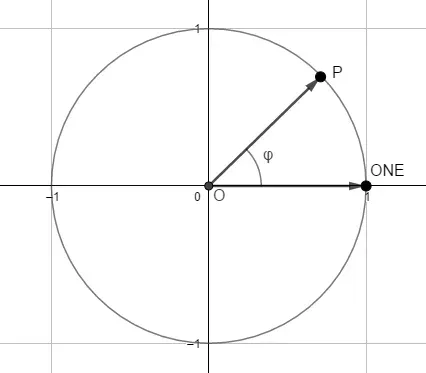
Let’s take note and enter another system of coordinates, which defines a point/ vector not by it’s projections, but by its length and orientation: this is called polar coordinates. In the following figure, the length of u is approx. 2.82 (2√2), while the angle 45°:

We’ll write it like this: u = (2.82; 45°), so having the semicolon as separator. And generally: u = (r; φ), where:

r: radius (or magnitude, modulus, length)

φ: direction, angle, argument. It is 0 for (a, 0), orientated, and increases on counterclockwise rotation. It is usually measured in radians, but we’ll skip this for now.

Note that u above can be a vector, but a p-number as well ;) We know already that:

c·(r; φ) = (c·r; φ) (15)

We can also derive the IDENTITY constant for our p-number multiplication (the p-number which, when multiplied with p, yields p). Without entering in too much details (I am already very lengthy ;), it is the scalar/ p-number 1:

IDENTITY = 1 = (1, 0) = (1; 0°) = ONE

We’ll call this ONE for convenience; see the figure above. Looking at formula (15), we can write it as:

(c; 0)·(r; φ) = (c·r; φ)

(because a scalar has angle 0). Let us extend this and define

(s; θ)·(r; φ) = (s·r; ?)

What we have done above is saying: “when multiplying any 2 p-numbers, the amplitude of the result will be the product of the 2 amplitudes involved”. Easy, right? The resulting angle is still to be defined.

Now, before defining full multiplication, let’s consider another problem: what would be the inverse of a p-number p? This is a number q so that

p·q = ONE = 1

Let be p = (r; φ) and q = (s; θ). Because of the amplitude rule above, it’s easy to calculate the inverse radius:

(r; φ)·(s; θ) = (1; 0) ⇒ r·s = 1, so s = 1 / r (the radius of the inverse is the inverse of the radius). But what should θ equal to?

To further simplify reasoning we’ll set r = 1, this way s = 1 as well. The problem now can be stated: given φ, find θ so as to have:

(1; φ)·(1; θ) = (1; 0)

Let us do a geometrical interpretation of this formula. All p-numbers with radius 1 are represented by points on a circle with radius 1 (what a surprise :) — or, by vectors of module 1, starting at the origin.

So the problem to solve is the following:

Given point ONE = (1; 0) and a random point P = (1; φ) on the unity circle, find a point P’ on the circle which is a good candidate for P inverse: P·P’ = ONE.

We’ll need some kind of symmetry here with respect to ONE, because P’·P = P·P’ = ONE (commutativity) is also a requirement (so P should also be the inverse of P’).

Now I am curious here, what would you have opted for…?

If you have a proposal, then I’ll give you one more hint to check for. When P approaches ONE, so its argument → 0, P’ should approach ONE as well. That’s because at limit, P = (1, 0) = 1, but the inverse of 1 is also 1. So what is your idea for P’?

From my part, I could not think of a better candidate than the reflection of P across the x axis. It’s angle will be negative here and φ’ = -φ.

OK, so now we have the inverse of a p-number:

(1; φ)·(1; -φ) = (1; 0)

We also note that, since φ + (-φ) = 0, the sum of the angles on the left hand side gives the angle of the sum. Now let’s take another random number, Q = (1; θ)

Question: how would you define the angle of product P and Q on the circle?

(1; φ)·(1; θ) = (1; ?)

I would keep the rule we’ve just seen, and put the sum of the angles as the result:

(1; φ)·(1; θ) = (1; φ+θ)

The following figure shows the discussed points.

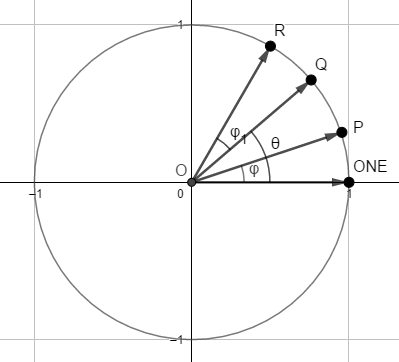
On the figure, φ1 = φ and R = Q·P. So the product of 2 p-numbers on the unity circle is another p-number, keeping it’s point on the same circle and adding the angles. For 2 random p-numbers, we have also to multiply their modules:

(r; φ)·(s; θ) = (r·s; φ+θ) (22)

Sorry, but I cannot help a small moment of admiration here: this rule is just simple, elegant and beautiful.

OK… but wait, you may say: if I have 2 p-numbers, say (2, 1) and (1, 3) like at the beginning, how can I multiply them? This radius — angle thing might be good, but how would I calculate them?

To switch from one coordinate system to another, so to (r; φ) from (a, b) or the other way around is not difficult. We’ll need some basic trigonometry.

In the figure above, observe that a / r = cos(φ), b / r = sin(φ), so

a = r·cos(φ) (25)
b = r·sin(φ)

What we are interested in the first place here is another formula for multiplication: given p = (a, b), q = (c, d), and p·q = (x, y), what are x, y in terms of a, b, c and d?

Let p = (a, b) = (r; φ)
q = (c, d) = (s; θ)
r = p·q = (x, y) = (r·s; φ+θ)

Let’s write (25) for q:

c = s·cos(θ)
d = s·sin(θ)

By applying (25) to r, we get:

x = r·s·cos(φ+θ) = r·s·(cos(φ)·cos(θ) — sin(φ)·sin(θ)) = r·cos(φ)·s·cos(θ) — r·sin(φ)·s·sin(θ) = a·c — b·d

y = r·s·sin(φ+θ) = r·s·(sin(φ)·cos(θ) + cos(φ)·sin(θ)) = r·sin(φ)·s·cos(θ) + r·cos(φ)·s·sin(θ) = b·c + a·d

So the product of 2 p-numbers can be written also as:

(a, b)·(c, d) = (a·c - b·d, b·c + a·d) (29)

Ladies and gentleman, we have almost arrived at the end of our journey. Or… well, almost. We still owe to prove the distributivity of multiplication over addition: p · (q + r) = (p · q) + (p · r). However, I’ll leave this to the reader. It is not difficult, and you have all the necessary tools to do it. Let’s see what have we achieved so far.

We have a set, let’s call it P, who’s objects are pairs of real numbers, e.g. p = (a, b).
We can visualize these objects, by points in a plane, or by vectors from an origin.
We can also calculate other inner properties of these objects, like modulus and argument: p = (r; φ)

We have 2 operations on this set:
Addition: (a, b) + (c, d) = (a+c, b+d)
Multiplication: (a, b)·(c, d) = (a·c - b·d, b·c + a·d), or
(r; φ)·(s; θ) = (r·s; φ+θ) (these 2 definitions are equivalent)

We know that this set extends the real numbers, got by setting b = 0: 
(a, 0) = a.

But what is this set good for ?

Let us observe that (a, b) = (a, 0) + (0, b) = a + (0, 1)·b
Let’s call this constant entity, (0, 1) say “i”. Question: what is the square of it?

i² = i·i = (0, 1)·(0, 1) = (0·0–1·1, 1·0 + 0·1) = (-1, 0) = -1

(Not that we are very surprised. (0, 1) is the point at distance 1 on the y axis, which has angle 90⁰: i = (1; 90⁰). When multiplied with itself, it rotates with another 90⁰, resulting in (-1, 0).)

Hmm… it seems to me to have met this thing somewhere…;) OK, you guessed it: this is the field of complex numbers !

Some notations are different, but you’ll probably forgive me for this. The set is called ℂ, and it’s objects are complex (not p-) numbers. The notation z = (a, b) is common: a is called the real part of z, while b the imaginary part. This comes from the axes of the complex plane: the horizontal is the real axis (since it has the real numbers), while the other called the imaginary axis. z = a + ib is an equivalent notation.

And what is i ?

i is nothing else than a complex number, the constant (0, 1), sometimes called the imaginary unit. You can see it’s point on the complex plane above. Because it’s angle argument is 90, it gives (-1, 0) = -1 when multiplied with itself: i² = -1. But this does not imply that it equals √-1. The other “definition”, found in some places, saying “i is defined by i² = -1” is an even bigger misnomer: partly because there is also another complex number which satisfies x² = -1: (0, -1) = -i. So i is just i, the imaginary unit (which is, obviously not needed for the definition of complex numbers). This is important.

Why is the notation a + ib so much used?

As shown above, a + ib is just another notation for the complex number (a, b). It follows from (a, b) = (a, 0) + (0, b) = a + (0, 1)b = a + ib. It is so appealing because you can make algebraic calculations with it like all elements were “real”, and substituting i² = -1, i³ = -i, a.s.o. If you look, for example at:

(a + ib)(c + id) = (ac — bd) + i(bc + ad)

(which is the complex product definition), it is like doing the normal algebraic operations and substituting i² = -1.

This is due to the fact that set ℂ is a field, and also an extension to the set of real numbers ℝ. There is nothing magical or surprising in this: it follows from the complex field properties.

So you can do many kind of algebraic manipulations with a + ib -like expressions (mostly the 4 basic operations), as long as you understand what you do. Beyond that, everything else is juggling (for example, better not try to calculate i^i if you don’t understand what that means.)

That is it! We come to the end of our journey. I hope you enjoyed it. Have fun in the imaginary world ;)