Given some two dimensional surface in R³, a sensible question to ask when getting acquainted with the beast is what the curvature is at any point (this would be sensible if you are approaching it from a differential geometer’s perspective; from a algebraist’s perspective you might as well ask what the colour 5 smells like).

What is Curvature?

The (Gaussian) curvature at a point is something that is very intuitive yet somehow quite hard to mathematically describe. Unsurprisingly, I will opt for the intuitive approach.

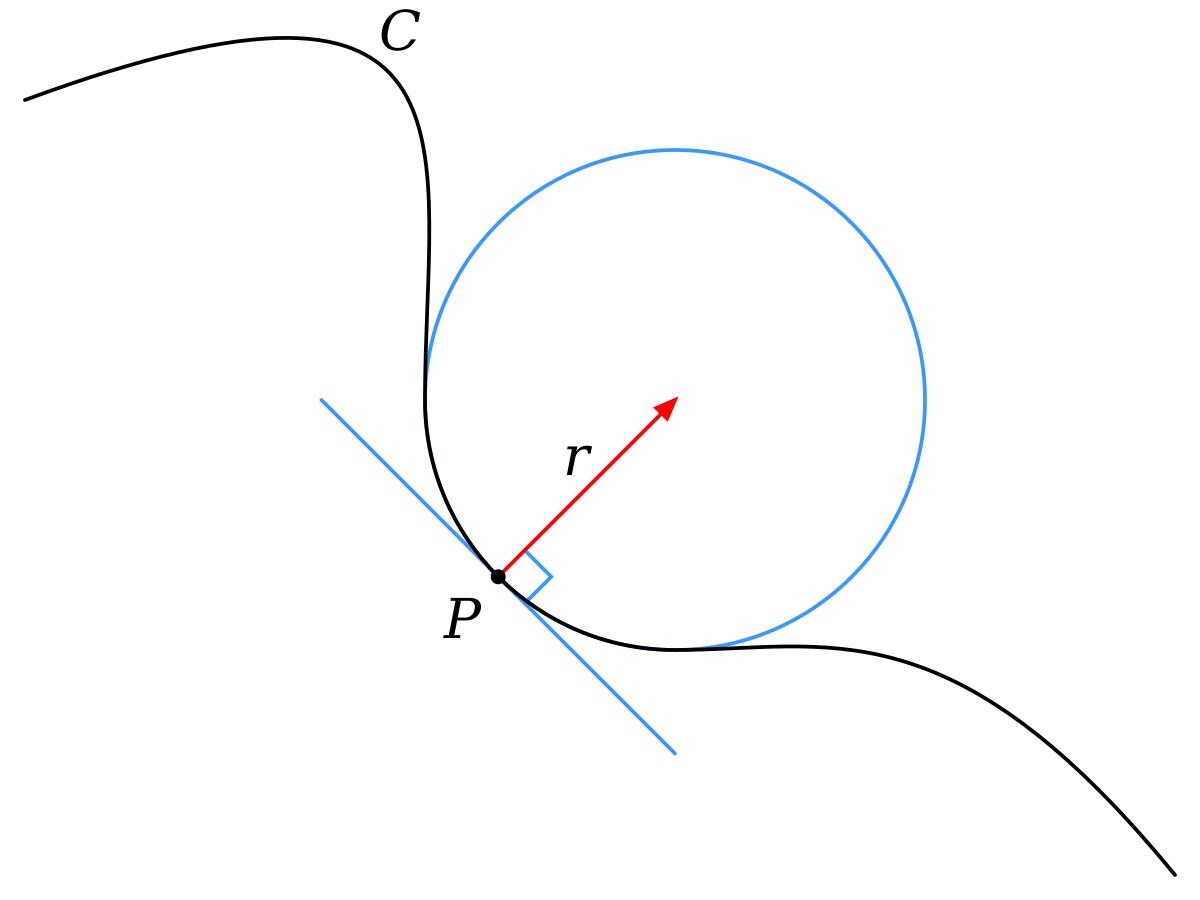
Imagine yourself on the surface in question. Each direction you look in will form a cross-section of the surface forming a curve. And each curve has a curvature associated with it. If you take a cross section of the surface in the direction you are looking in then the curvature is the inverse of the radius of the osculating circle.

An osculating circle is basically the circle that fits the most snugly to the curve at that point. So the curvature at P is 1/r.

Now we have an issue:

In mathematics we like to make things as general as possible but here we will need to make a choice of the direction of normal unit vector. (i.e. which way is up.) It will turn out that this will become somewhat irrelevant but it makes our lives easier for now.

The sign of the curvature at P is going to be positive of the centre of the osculating circle is ‘below’ the surface and negative if it is ‘above’. Here below and above can be determined by looking at the normal vector.

Now we are in a position to define Gaussian curvature. So remember, you are standing (upright) on the surface and we will choose you to be the normal vector. Then there is a direction of greatest curvature (most positive) and least curvature (most negative). Note that the direction of greatest curvature (least) can still be negative (positive).

The curvature in these directions are known as the principal curvature, called κ₁ and κ₂.

Now the Gaussian curvature K at the point you are standing at is simply:

Examples of Curvature of Surfaces

Let’s play around with this a bit to get some intuition.

The easiest to consider is a sphere. If we stand on the surface, the cross-section of the sphere in each direction we look in will be a circle. Moreover, it will be the same circle in each direction and irrespective of where you are standing. (Ah the beauty of symmetry!)

The osculating circle to a circle is (pretty intuitively) the circle itself. So the curvature in any direction is 1/R where R is the radius of the sphere. Since the curvature is the same everywhere, the principal curvatures are both 1/R, therefore the Gaussian curvature everywhere is 1/R².

Since the curvature is constant and positive everywhere, the sphere is known as a surface of constant positive curvature.

Considering a flat plane. The curvature in any direction is 0 and as a result, the Gaussian curvature is 0. Easy enough and pretty intuitive.

Lastly, consider a saddle point (Pringle shaped):

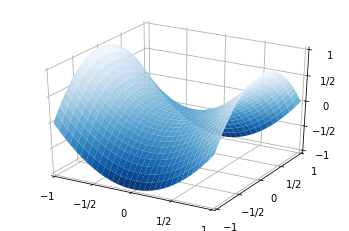
Here we have one direction that has positive curvature and one that has negative. Therefore it has negative Gaussian curvature at the origin.

Side Note:

If we extend the saddle point to the hyperbolic plane, we get a surface of constant negative curvature.

We can have surfaces whose curvature changes sign. One example is the torus:

Now here comes the fun stuff.

Theorema Egregium

Literally means remarkable theorem. This is due to Gauss in 1827.

It states that Gaussian curvature is invariant under local isometry.

An isometry is a map that preserves distances. More formally speaking, it is a map, f, between two metric spaces (this can be generalised to Riemannian manifolds but that is a lot more work) (X, d_X) and (Y, d_Y) such that for all points a and b in X, we have

Trivial examples of such are automorphisms (maps from a space to itself) that rotate or reflect in some symmetrical way.

Another example is bending a sheet of paper into a ‘U’ shape. ‘But!’ I hear you cry, ‘Surely the U shape has negative curvature?’

Well not quite. The most negative direction is up and down the ‘U’ but the other principal direction is along the base of the ‘U’, which has 0 curvature. Therefore the curvature is 0, which is the same as the flat sheet of paper. Gauss is still right.

Now how does this link to eating pizza?

Suppose you have your pizza with your favourite toppings. If you pick up a slice then we all know the pizza will flop down and your toppings will fall off and ruin your day.

In comes Gauss to save the day.

Consider the pizza slice as a surface (it has some depth but we will ignore it). A slice is basically a small part of a plane and so has constant zero curvature. For simplicity, let us define the crust direction is the direction that runs in the direction of the crust and the radial direction is the direction that runs perpendicular to the crust and goes through the centre of the pizza along the radius.

Now when we pick up the pizza, the crust has enough structural integrity to keep the curvature in the crust direction at 0. and due to gravity, the radial direction curves down giving it positive curvature. The Gaussian curvature is still 0 and Theorema Egregium still holds and the pizza toppings are still on the floor.

Now here is the genius part. If we fold the crust in half, we force the crust direction to have negative curvature. But since the Gaussian curvature has to remain 0, this forces the radial direction to have zero curvature. This mean that the pizza won’t flop down and your toppings will stay on the pizza. Success!

This trick may not be new to a lot of you but I think it’s pretty interesting to see why it actually works.

Another interesting corollary of Theorema Egregium is that you can’t draw a (flat) map of the world that preserves distances. This is because the world is a sphere (or at least sphere-like) and so has positive curvature and a map has 0 curvature. Since 0 is not positive, you can’t construct an isometry between the two and so you can’t make a map that preserves distances.

All this talk of pizza makes me really want one now!