The twin prime conjecture states that:

There are infinitely many twin primes

A twin prime is a prime that differs from another prime by two. A set of two primes that differ by two are called a twin prime pair. The first twin prime pairs are:

(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73), (101, 103), (107, 109), (137, 139), ...

The prime pair (2,3) is not considered to be a twin prime set because they differ by one instead of two, thus they are more closely spaced than other all other twin primes.

Origins

Although Euclid in 300 BC proved that there are infinitely many prime numbers, the question of whether there are infinitely many twin prime numbers did not come about until 1849 when Alphonse de Polignac (1826–1863) conjectured that for every natural number k, there are infinitely many primes p such that p + 2k is also prime. The twin prime conjecture is the special case of k=1.

Next, at the International Congress of Mathematicians in 1912, Edmund Landau(1877–1938) included the twin prime conjecture on a list of open prime-related problems in number theory now known as Landau’s Problems. The other three problems he listed were:

• Goldbach’s conjecture: Can every integer greater than 2 be written as the sum of two primes?
• Legendre’s conjecture: Does there always exist at least one prime between consecutive perfect squares?
• Are there infinitely many primes of the form n²+1?

All problems remain open to this day.

The first Hardy-Littlewood conjecture (1923)

A similar, but stronger twin prime conjecture was later made by G. H. Hardy(1877–1947) and J.E. Littlewood (1885–1977). Known as the first Hardy-Littlewood conjecture, it is concerned with prime constellations, defined as

A prime constellation of length k is the shortest possible prime k-tuplet.

A prime k-tuplet is a repeatable pattern of primes that are as close together as possible. The twin prime conjecture is the case (p, p+2). Analogous to the prime number theorem, the first Hardy-Littlewood conjecture essentially states that the asymptotic number of prime constellations can be computed explicitly.

Results

In 2013, Yitan Zhang (1955-) proved that for some integer n > 70,000,000, there are infinitely many pairs of primes that differ by n. That is, he proved that there are infinitely many prime pairs that differ by less than 70,000,000.

“That’s only a factor of 35 million away” — Dan Goldston

The results was published in the Annals of Mathematics, and can be found in:

• Zhang, Y. (2014). Bounded gaps between primes. Annals of MathematicsSecond Series Vol. 179 (3). pp. 1121–1174.

Within a year of Zhang’s announcement, spurred on by a collaborative effortinitiated by Terence Tao (1975-), the bound of 70 million has since been reduced to 246 (!). To date, in other words, we know that there are infinitely many primes which differ by less than 246.

Twin prime functions

With the exception of the primes 2 and 3, every prime may be generated by the function f(n) = 6n +/- 1, including twin primes. To illustrate one of the patterns that twin primes create, first consider the graph of the function |6n+1| below:

Next consider the function

For various values of m, this function generates linear graphs that intersect the function |6n+1|. For the first twin prime pair (3,5):

And for the second twin prime pair (5,7)

..and all twin prime pairs in our list above:

The values of m for each twin prime function is obtained by dividing 6 by the even number number in between the primes in each pair. So, for the list of twin primes above:

(3,5), (5,7), (11,13), (17,19), (29,31), (41,43), (59,61), (71,73), (101, 103), (107, 109), (137, 139), ...

We obtain

4, 6, 12, 18, 30, 42, 60, 72, 102, 108, 138, ...

Which produces

m = 3/2, 1, 2, 3, 5, 7, 10, 12, 17, 18, 23, ...

Together, the twin prime functions form a web of intersecting graphs which transform the one-dimensional number line into a two-dimensional plane:

The pattern is more easily discernible for larger values of n. See below for the first twenty twin prime functions from n = 0 to n = 14,000:

As we move further up the number line (y), we see clearly the large gaps that exists between twin prime pairs, e.g. between the twin prime pairs (659, 661) and (809,811), (881, 883) and (1019, 1021) and so on.

Does the pattern go on to infinity? Perhaps 🤷🏻‍♂️

The largest twin primes found to date, with its 388,342 decimal digits, is:

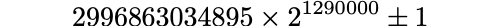
Those interested in a more elaborate introduction to twin primes are encouraged to look up the video “Twin Prime Conjecture” by Numberphile. More advanced readers may be interested in the lecture “Small and Large Gaps Between the Primes” by Terence Tao, also available on YouTube.