Infinity in Numbers — Leonhard Euler

My approach to his work will be both in terms of results, historical remarks, and some curiosities along the way. Reading this essay, hopefully you will get a feeling of timelessness and a glimpse into the beauty of the elegance, art, and eternal truth of mathematics. I will try to blend stories, facts, and easy-to-follow mathematical proofs (as Euler would have written them) in full detail so that in the end, the reader should be left with a good feeling and a desire to learn more. The results shown here have been chosen carefully but are in no imaginable way exhaustive. In fact, it has been estimated that almost a third of all the science and mathematics written in the eighteenth century, was by Euler! We will first get a feel for his origin, then we shall immerse ourselves deep into his thoughts and beautiful mathematics.

Early Life

Euler was born in Basel on 15 April 1707. His father was a friend of the Bernoulli brothers, including Johan Bernoulli (1667–1748) who at that time was regarded as one of the best mathematicians in the world. Johann would come to influence young Euler in the years to come.

Euler received a Master’s degree in philosophy (those day’s science) in 1723 even though he was also studying Theology. In that period Euler spent his Saturday afternoons getting lessons from Johan Bernoulli himself. Johan quickly discovered that Euler had a flair for math, and convinced his father, that Euler should pursue mathematics and not theology.

In 1727 young Leonhard entered the Paris Academy Prize Problem competition. The problem that year was how to best place masts on a ship. Euler was placed number two in the competition only surpassed by Pierre Bouguer (a.k.a the father of naval architecture). Euler had at the time never seen a ship! Later, he would win the competition 12 times over. Around that period, he tried to get a position at the University of Basel but was rejected (a huge mistake by the university of course). In the meantime, Johan’s son Daniel Bernoulli was working at The Academy of Sciences in Saint Petersburg and got Euler a position there a little later.

Towards Infinity

In the middle of the 17th century, a challenge was raised by the mathematical community: find the exact value of the following “infinite sum” (mathematicians call this sort of beast a series)

Note that the more terms one calculates, the closer to a certain value of about 1.644934 one comes. This is called convergence, and mathematicians of the day knew that this series converges. The hard part was to find what is called a “closed-form expression” of it.

At this point, you might be thinking: an infinite sum? That doesn’t make any sense at all... Well, formally an infinite series is not a sum but actually what is known as a limit.

Imagine that you have to paint a wall. Each day you decide to paint half of what’s left to be painted. So you start painting and on the first day, you paint half of the wall, on the second day you paint half of what’s left which is a quarter, and so on. Now, two important facts come up quite naturally.

In applying this strategy,

1. It is not possible for you to paint more than the area of the wall
2. Given an unknown fraction of the wall (arbitrarily close to 1), you can be sure to paint more than that if you continue to paint

You can then (a little hand-wavy I admit) argue that if you had infinitely many days to paint the wall in this fashion, then when you reached infinity you would have painted it all! Because if you had painted more, then it would have violated the first rule above, and if you had painted less then it would have violated the second rule.

This is the essence of convergence. And in fact, what you have just convinced yourself about is that

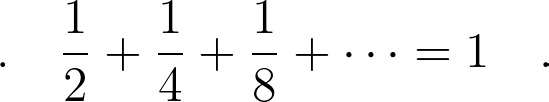
Where the three dots on the left-hand side means “keep going like this" to infinity. Throughout this article, we will prefer this notation where it makes sense rather than a more compressed notation because I don’t assume that the reader knows much mathematical notation and if you do, then you understand this as well. Now that we understand the meaning of convergence, let’s move on because we have a very famous series to calculate!

Prominent mathematicians of the day had tried to solve The Basel Problem, including the Bernoulli brothers and Leibnitz, but nobody could find the true value of this infinite series of reciprocal squares.

Before I give you Euler’s proof of what this value turns out to be, we need a little background. Many of Euler’s proofs involve infinite series. In particular, a type of power series known as a Taylor series will crop up now and then, so I think we will be best off by recalling what that is.

The Maclaurin Series

First of all, if you don’t know what a power series is, then you can think of this as an infinite polynomial i.e.

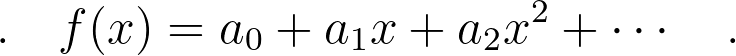
Let’s say that you’re given a function f. Even though your function is not a power series, you could think about how well we could approximate it by a power series.

Let’s pretend that your function actually can be written as a power series. All we need to do is find the possibly infinite number of coefficients. No problem! We grab a warm cup of coffee and think about it for a while. You soon realize that if you set x=0, then you get the constant term, and since

If you differentiate your power series and set x = 0, then you get the linear coefficient, if you differentiate two times, divide by 2, and set x=0, you get the quadratic coefficient and so on.

You need to divide by n! when you extract the nth coefficient because you multiply by a decreasing power for each time you differentiate. You have now discovered a general formula for the nth coefficient of a possible power series of f. In fact, many functions can be represented this way. A more concise notation is the following:

Where the notation in the numerator means f differentiated n times and the Greek letter Σ (called sigma) means sum over n from 0 to infinity. This is known as the Maclaurin series expansion of the function f (since the center of approximation is 0). A more general series of this sort is known as a Taylor series but it is the same idea.

We only need to understand Maclaurin series in this article. It is an amazing fact that when this series converges, then it is actually equal to f. Now we are ready to see what Euler did to the Basel problem. In 1734, Euler came up with the following proof.

Euler’s Solution to the Basel Problem (1734)

First, he recalled the Maclaurin series expansion of the sine function. It turns out that the sine function (yes that trigonometric nightmare from high school that had something to do with circles and right triangles) can be written as a power series.

Then he divides through by x to get

Of course, Euler wouldn’t be Euler if his proofs didn’t have creative sparks of genius. The next step in the proof he gives you just that.

Euler argued that the left-hand side of the above can be seen as an infinite polynomial, and we all know that polynomials can be factored into a product of linear factors of the form

where c is some number and the r’s in the denominators above are the polynomial’s roots (also called zeros). The fact that any polynomial can be written like this is called The Fundamental Theorem of Algebra and is a very important result.

Euler argued that this theorem was also true for some “infinite” polynomials as the power series above.

If the reader is willing to believe this, let’s move on.

Since the constant term of the series of the sine function is 1, it is clear that c = 1. We now have

Euler asked himself what the zeros of this function are, and of course, they are the zeros of the sine function, and those are whole number multiples of π. Therefore,

The second equality comes from multiplying out neighboring terms. Now another brilliant thought is needed.

Euler of course recognizes the square numbers hiding in the denominators of the quadratic terms above and wants to “free them” from the product. What better way to do this than to simply multiply out this infinite product? This sounds dreadful, but we really just need the first two terms of the resulting polynomial, so you can wait with the coffee break.

Obviously, the constant coefficient is 1. How about the second term? Well, for each coefficient in the corresponding infinite power series, we need to choose only one non-constant term and all the 1’s from the other terms in the product. We then obtain

Now Euler compares this with the Taylor expression from the beginning. Namely,

and if these two expressions are true, then the right-hand sides must be equal as well — as functions.

Euler concludes that their constants would have to be pairwise equal as well. That is

Or stated another way:

This is Euler’s proof of this theorem. Mathematicians write this in a more condensed form:

The remarkable result made Euler instantly famous but what is the big deal about this? Well, first of all, it had defied all the best mathematicians for almost a century, but it is not just that. If you take a look at the two sides of the identity above, then you might notice that the left-hand side is about reciprocal squares of whole numbers but the right-hand side is an expression involving the number π which of course is any circle’s circumference to its diameter.

So, on the left, we have an expression containing the reciprocal squares of all the natural numbers, and on the right an expression containing information about circles. That was indeed unexpected. The geometrical reason behind it is also interesting and can be explained by some laws of triangles and the fact that an infinitely big circle (we should take a limit here really, but this sounds better) is linear in a neighborhood around a point, but I am afraid that we digress and need to get back on track.

Euler, of course, didn’t stop here. He calculated the sum of the reciprocal of the fourth powers, sixth powers, and so on and made a general formula for this calculation when the power is even. He couldn’t find a closed-form expression for any odd powers though. And to this day, this is an open problem. Nobody knows the true value of the sum of the reciprocals of the cubes for example and whoever solves this will become extremely famous.

There is a small detail in the proof above, that you may have thought about. Namely, that the proof depends on the statement that the sine function can be written as an infinite product over its zeros. This is by no means obvious and in fact, it does need an argument.

It turns out that the right argument came along with some rich theory from complex analysis and the mathematician Karl Weierstrass (1815–1897) about one hundred years later. But in fact, Euler’s sixth sense was right in that many functions have this property, including the sine function of course (but not all).

A Bridge Between Two Worlds

Euler wasn’t done studying these interesting series and to generalize the problem, he defined the following real-valued function:

It turns out that this function only makes sense when s > 1 otherwise the series diverges. Note that in the special case s = 2, we have The Basel Problem from above. Euler then goes on to find and prove yet another pearl called an Euler product in his honour, namely

Where the sum on the left-hand side is running over all natural numbers and the product on the right-hand side is over all prime numbers. This holds true for all real numbers s > 1. In a more compressed matter, it states

I will not provide a proof of this proposition here, but it is not hard to prove. You can prove it by a combination of the fact that the so-called geometric series has a closed-form i.e.

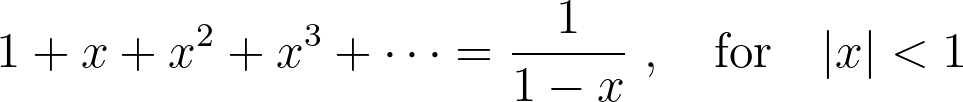
and the fact that each natural number can be written as a unique product of (not necessarily different) primes (up to commutation). The unique prime factorization property is known as The Fundamental Theorem of Arithmeticand is again a very important property of the primes. The Fundamental Theorem of Arithmetic was first discovered by the Greeks, but 2000 years later it was used by Euler to obtain this result which started the field of Analytic Number Theory which is basically the study of whole numbers using real and complex analysis.

The function, together with its Euler product, is like a dictionary between the additive world and the multiplicative world. The fact that this function can be expressed in both worlds makes it very interesting and one might think that one could use it to translate knowledge from one universe to the other and vice versa. More about that in a moment.

Another nice result that kind of falls out of the blue, is that this is yet another proof that there are infinitely many prime numbers, because if we let s → 1 from above on both sides, then certainly the left-hand side blows up as it becomes closer and closer to the harmonic series, and the right-hand side would also have to go to infinity because of the equality. But this could only be so if there are infinitely many prime numbers. Because if there were finitely many, then the product would not diverge.

This is the second proof of this fact. The first is credited to Euclid. The amazing thing about this proof, however, is that it is so different from Euclid’s. Euler used limits and functions from analysis and Euclid used a proof by contradiction that showed a way to always generate the need for another prime give a finite amount of primes.

Euler kept returning to this function throughout his life proving the Basel Problem in many different ways. As mentioned above, he discovered the relationship between the multiplicative and additive world through this interesting function and he obviously regarded it as important but it would take about 100 years and another genius to reveal just how important and interesting the function really is. Nowadays this function is named after him and is called The Riemann Zeta Function (that is if one considers it as a complex function of a complex variable) after Bernhard Riemann.

It turns out that other functions have Euler products (the so-called L-functions) and that these functions display a similar behavior as the zeta function but I’m afraid that that is out of the scope of this article.

The Riemann Zeta Function is worth a whole article in itself and is a very interesting study on its own. The function is surrounded by mystery and there is a great problem associated with it — the so-called Riemann Hypothesis.

If you prove this, you will, not only, get a price of a million dollars, you will be remembered in the same way that we remember Archimedes, Euclid, Euler, and Gauss. You would be remembered as the one who solved the holy grail of mathematics.

What is the problem again? Well, it turns out that if one considers Euler’s zeta function as a function of a complex variable, and makes what’s called an analytic continuation so we can evaluate it at complex numbers with real part less than 1, then the function has zeros (the numbers that it maps to zero). This is the function called the Riemann zeta function. It is important to note that this function is the same as Euler’s zeta function if one restricts it to the real numbers greater than 1. When one studies the zeros one finds that the zeros seem to lie quite neatly on two straight lines. One subset of the zeros lie regularly on the real line at the negative even integers -2, -4, -6, …. This is proved.

The other zeros seem to all lie quite irregularly on a vertical line in the complex plane. At the line Re(s) = 1/2. This is the problem.

Prove that all the non-trivial zeros lie on this line.

The reason why we would like to prove this result so badly is that using Euler’s dictionary between the two worlds, the Riemann Hypothesis says something very specific about how the prime numbers are distributed on the number line.

Euler didn’t consider this because complex analysis wasn’t really developed at his times but he would certainly have recognized the beauty of Riemann’s work on this subject had he been alive in 1859 when Riemann’s paper on the subject emerged. In the next part of our story about Euler, we will investigate what’s been called the most beautiful equation in mathematics and along the way explain geometrically why when we multiply two negative numbers, we get a positive number.

We’ll finish off this part with a quote.

The study of Euler’s works will remain the best school for the various fields of Mathematics and nothing will replace it ~ Gauss