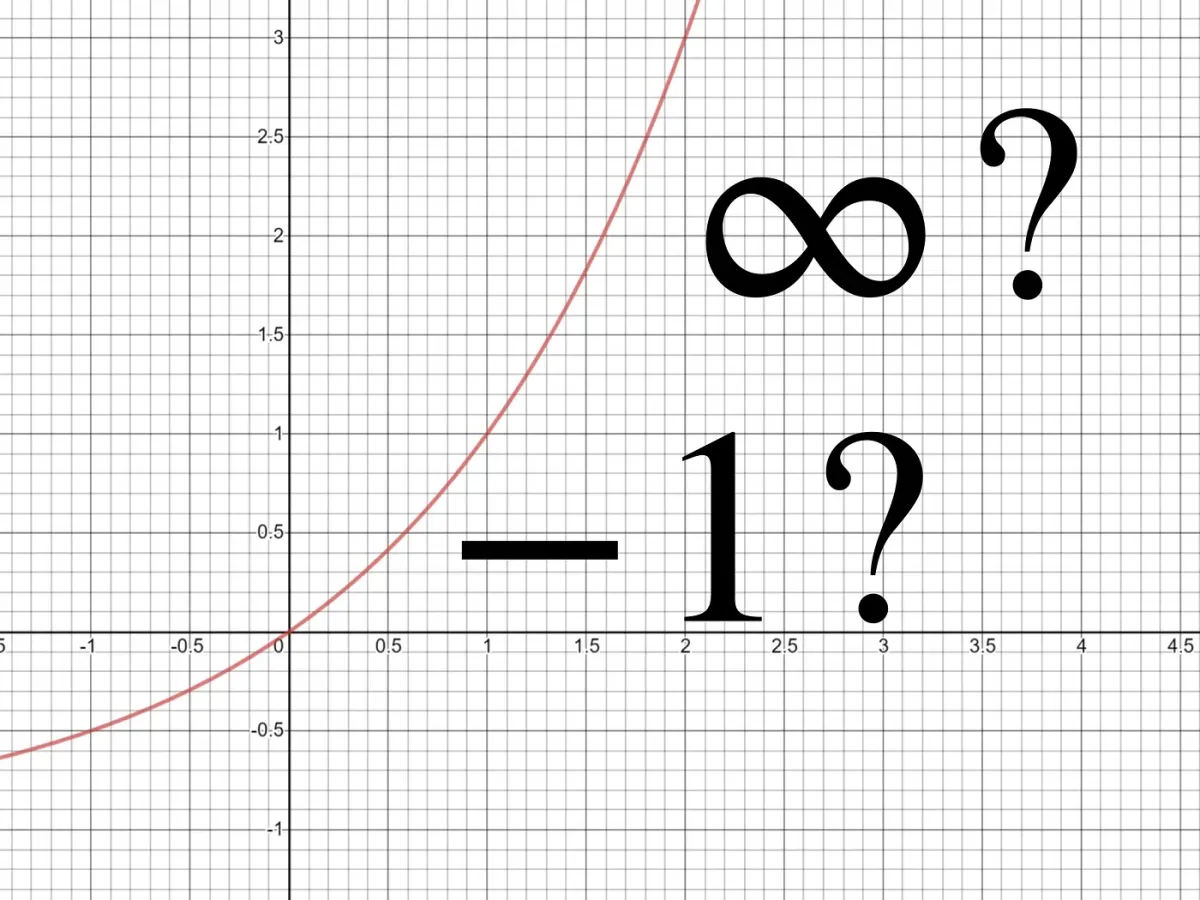
The Short Answer

To satisfy your curiosity and save you from the mathematical jargon, the simple explanation is just:

x = 1 + 2 + 4 + 8 + … 
x = 1+ (2 + 4 + 8 + …)
x = 1+ 2(1 + 2+ 4 + 8…)
x = 1+ 2x
x = -1

This is almost the exact same method you would use for a convergent infinite series, by taking advantage of the common ratio of the sequence and the nature of infinity. But while convergent series, like 1/2 + 1/4 + 1/8 + 1/16…, can easily be visualized and comprehended, divergent series are much more incoherent.

Nonetheless, if you would join me in the scenic route, perhaps we can stumble upon a few more answers and — even better — more insightful questions.

Divergence vs Convergence

A convergent series is one whose sum approaches a limit.

For instance, the convergent series 1/2 + 1/4 + 1/8 + 1/16 + … clearly approaches a certain limit, which is 1, as made apparent by the geometric illustration below.

Partial Sums

We can also differentiate divergence and convergence by their partial sums. As the name suggests, a partial sum is a sum of a part of a series. We can express the partial sum of the first n terms of 1/2 + 1/4 + 1/8 … using the formula for a geometric series.

Applying that formula, we see that the partial sums of a convergent series seem to approach one, which is made even more evident by graphing it.

In the case of divergence, however, the partial sums do not approach a value but extends to infinity

‘Rules’ For Calculating Infinite Divergent Series

Although doing so is comparatively less straightforward, it is still possible to get the sum of a divergent series — as long as we follow a few rules.

Regularity

A summation method is regular if the sum it gives for a convergent series is the limit of its partial sums

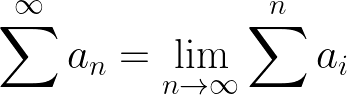
Linearity

To be linear, sums must be distributable and factorable

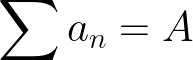
In a linearity, terms of a summation of equal length can be grouped.

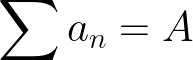
Stability

Stability is present when terms can be “extracted” from a summation

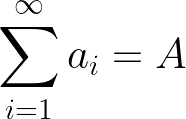
Applications to power of two

x = 1 + 2 + 4 + 8 + … 
(1) x = 1+ (2 + 4 + 8 + …)
(2) x = 1+ 2(1 + 2+ 4 + 8…)
x = 1+ 2x
x = -1

Taking the long route has its benefits. If you paid attention, you would notice that our initial solution is not completely regular. This is because the limit of the divergent series is infinity, and yet we gave a finite value as an answer. Yet we can show that it does comply with linearity and stability.

(1) x = 1+ (2 + 4 + 8 + …)

In (1), we were able to extract a term from the summation, this is equivalent to

Hence we can say that the summation method is stable.

(2) x = 1+ 2(1 + 2+ 4 + 8…)

With (2), we were able to factor out 2 from a summation, which is the same as

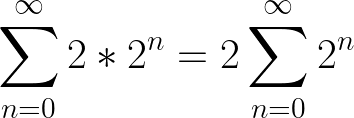
And finally, this shows that the series is linear.

The Long Answer

So given this, we can say that 1 + 2 + 4 + 8 + … is not completely -1, because the summation method we used — although linear and stable — is not totally regular. Totally regular summations would say infinity is an answer.

What’s the real answer? Depends which requirement you prioritize.

But it’s not always about finding the answer, is it? Just grappling with infinite divergent series can lead us to some interesting insights, and even — as Leonhard Euler has shown us — to profound discoveries on mathematics as a whole.

All it takes is time and patience.

Source

Sums Of Divergent Series. Brilliant.org. Retrieved July 1, 2020, from https://brilliant.org/wiki/sums-of-divergent-series/