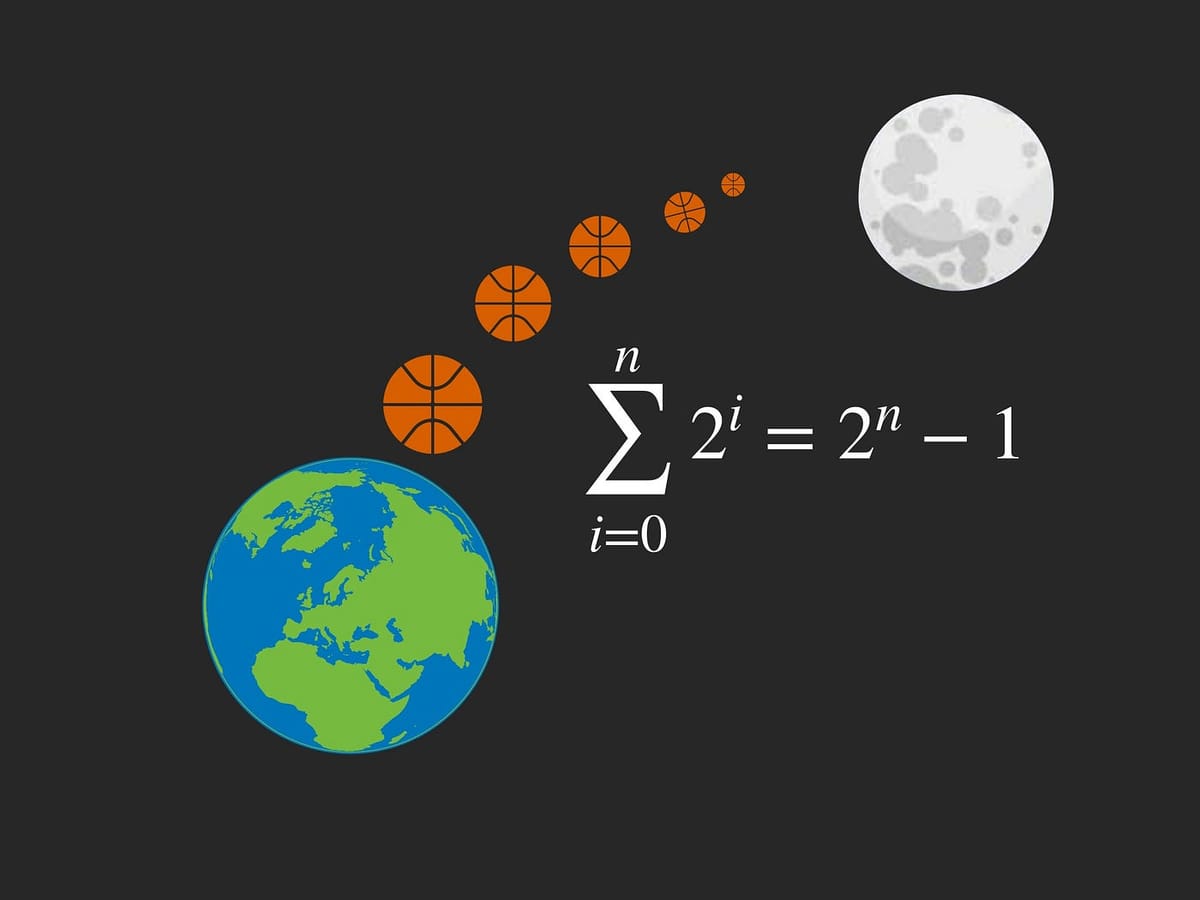
⚠️ Disclaimer: Vectors are not drawn to scale as they should be

If I drop a ball, and it falls at a constant velocity v, what will its velocity be after hitting the ground? That’s pretty straightforward to answer. Disregarding friction and air resistance (and the fact that objects don’t fall at a constant speed), we can say that the ball will bounce back with the same speed, but in the opposite direction. Remember, when describing velocity — a vector — we must account for both magnitude and direction.

As mentioned, that was pretty easy. But let’s spice things up a bit. What if we dropped two balls simultaneously — one stacked on top of the other. Assuming, again, that the objects fall at a constant velocity, what will be the speed of the ball on top after bouncing back?

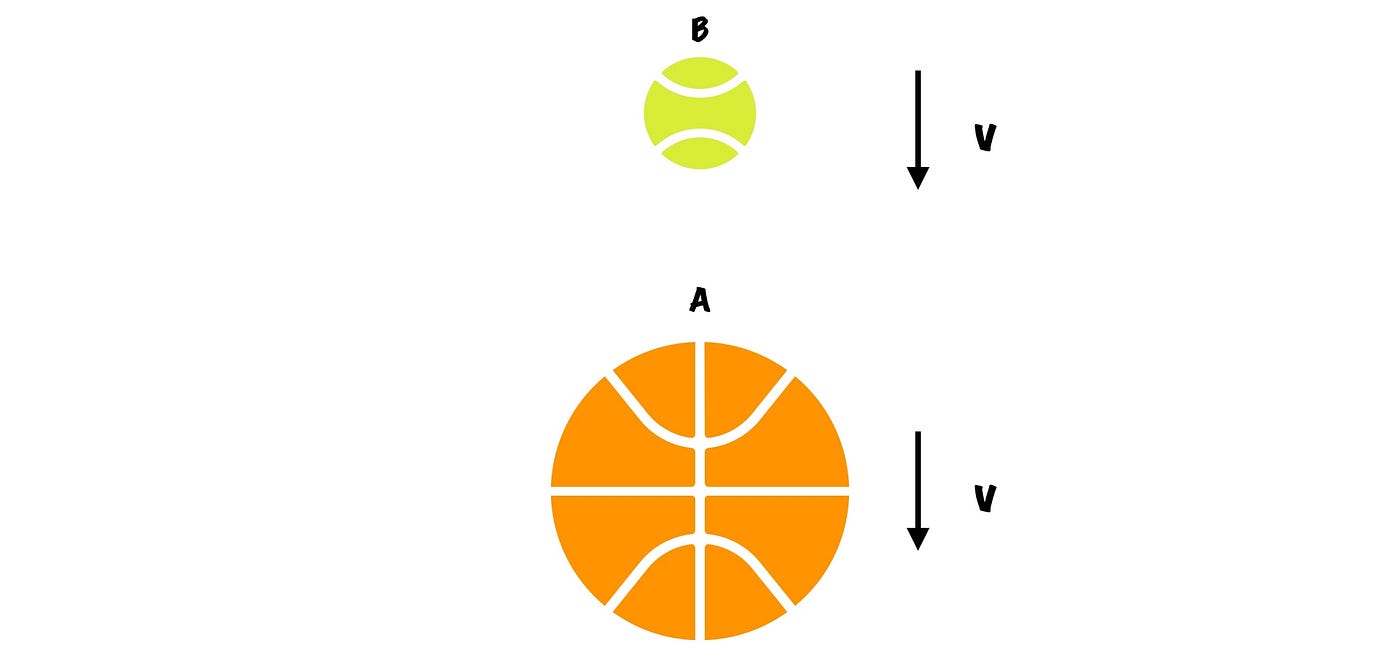
For simplicity, let’s say that the ball on top is small enough to have a negligible effect on the other ball (imagine dropping a tennis ball atop a basketball).

It helps to consider problems like these step-by-step and in terms or reference frames. Let’s see how that would work.

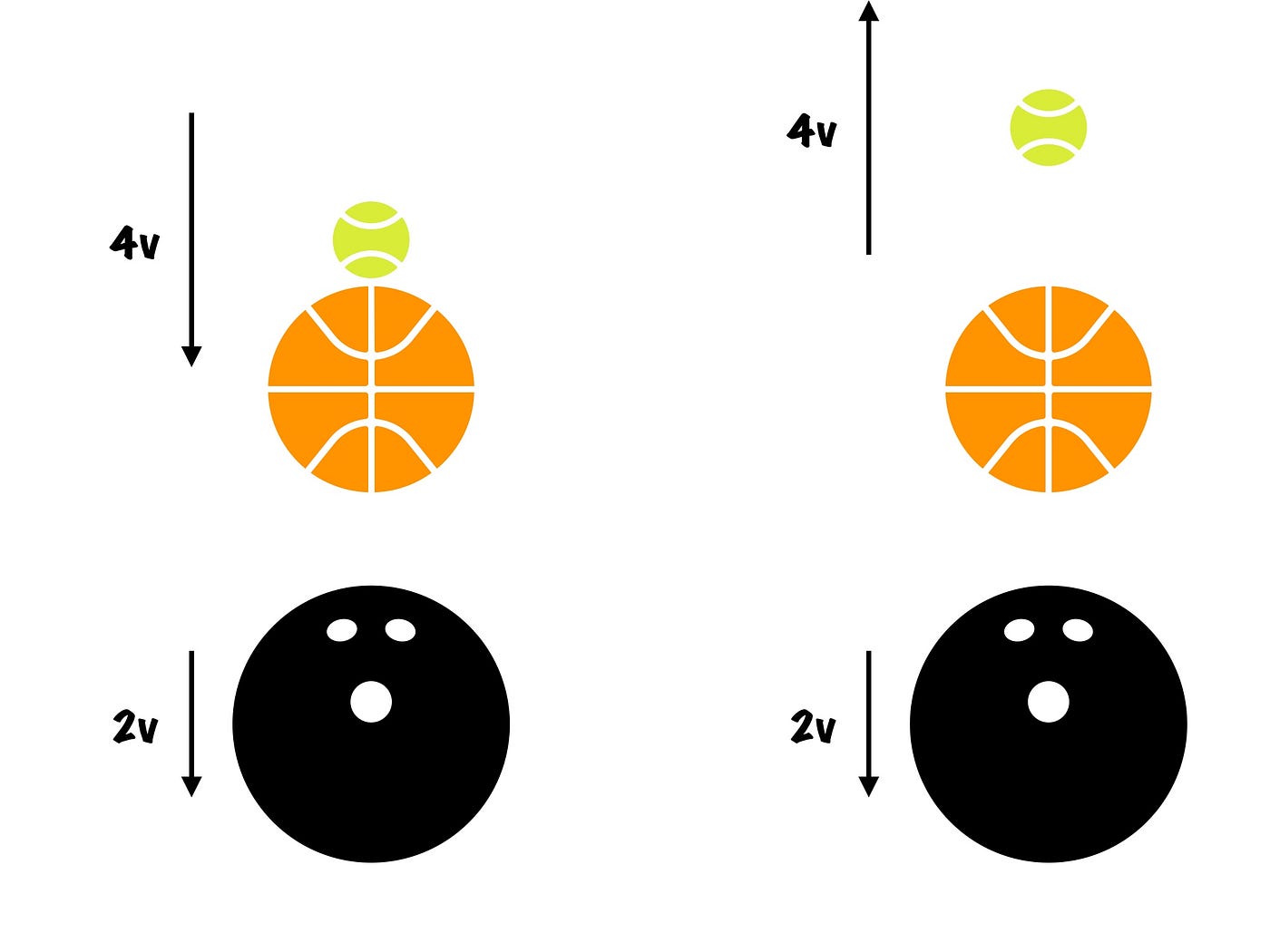
Step 1: Ball A hits the ground

Assuming there is space between the balls, that the first ball will bounce back at speed v.

Step 2: Collision

Next, the balls collide. At this point, it would already help to make use of reference frames. Let’s consider things from the perspective of Ball A. In this frame, Ball B would be approaching Ball A (which is stationary) at 2v. Therefore, after hitting Ball A, Ball B would bounce back at 2v as well.

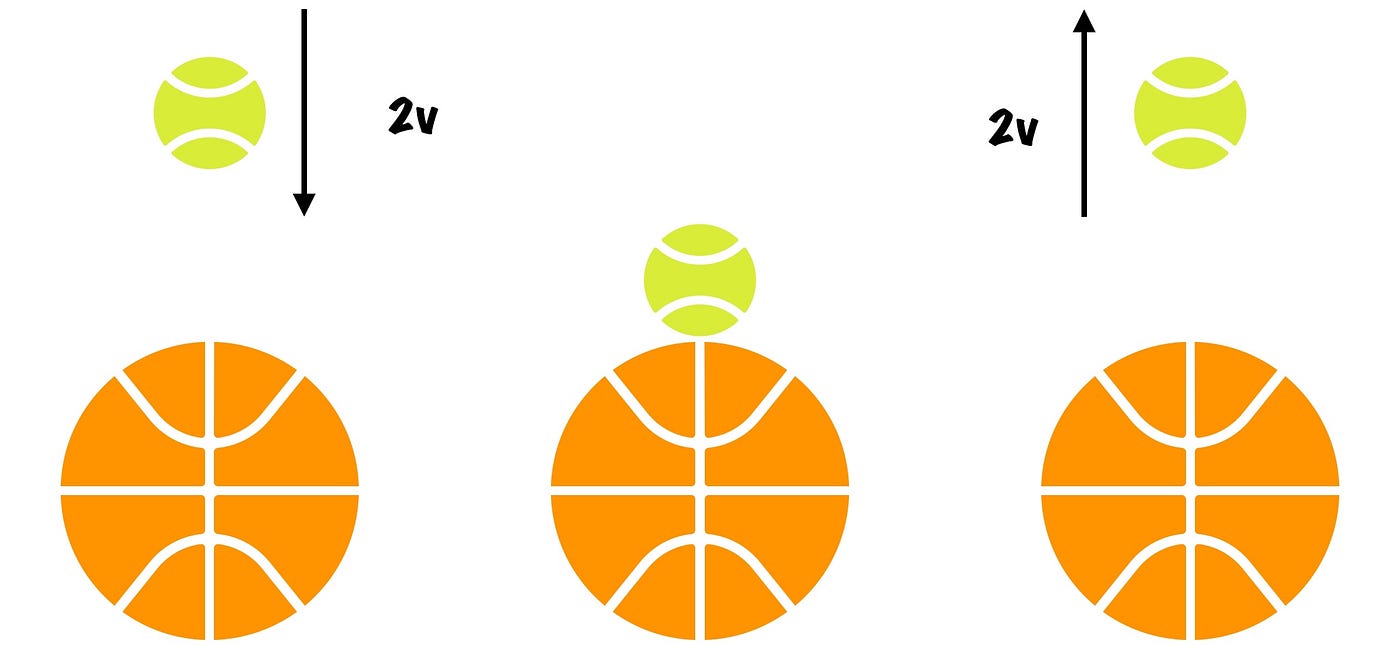
Step 3: Back to our reference frame

But remember, we are still viewing things from Ball A’s perspective. Since Ball A was moving at a velocity of v upward, its reference frame is -v slower than our reference frame. Hence, to convert back is to simply add v to both ball’s velocity.

From this, we can see that Ball B will bounce back at a speed of 3v.

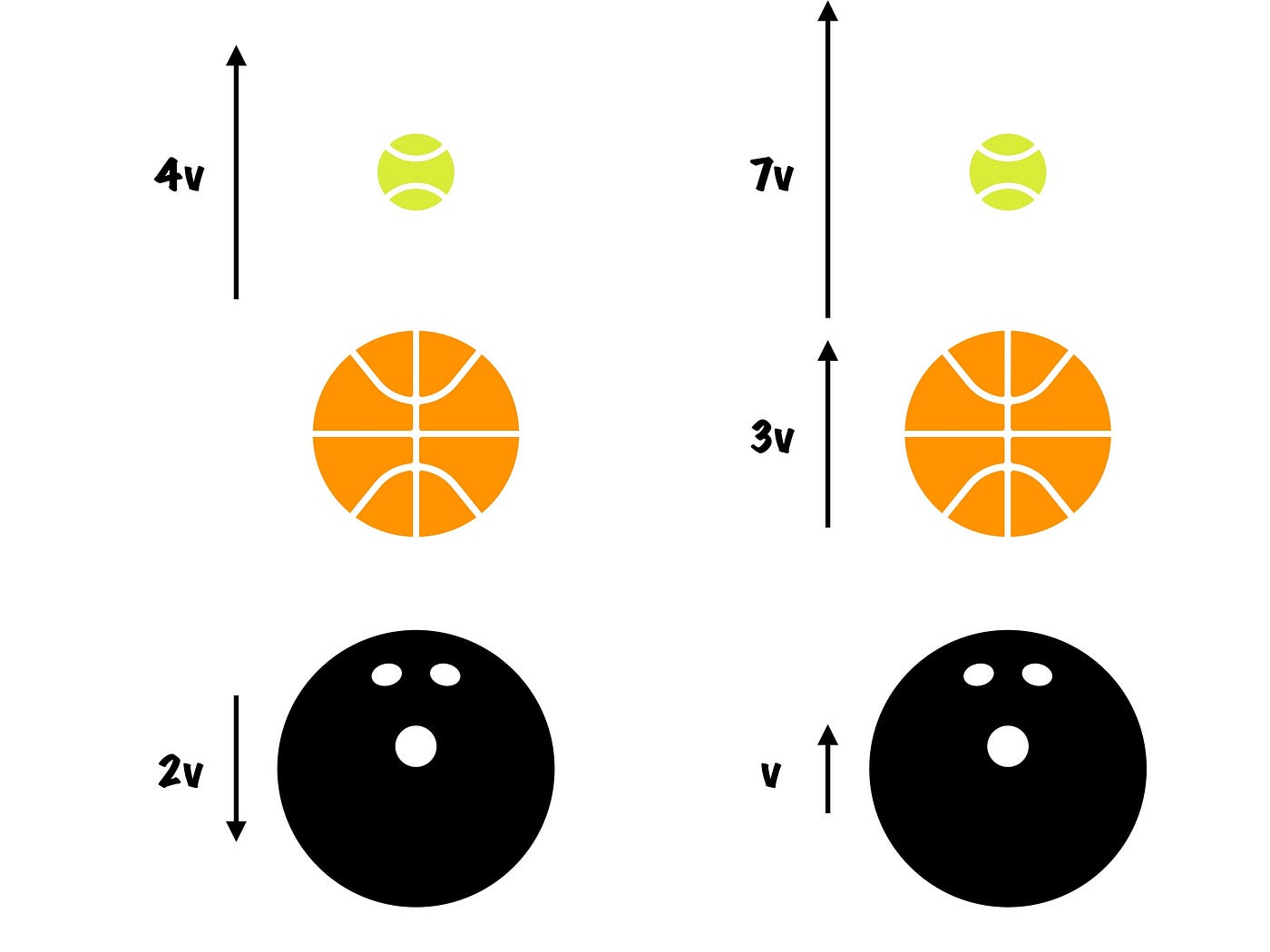
This was easy enough. But what happens if we add a third ball? Well, we can simply repeat the recursive process: convert to the previous ball’s reference frame, do our calculations there, then convert back to our reference frame to get the final velocity. The process is illustrated below.

Change to Ball B’s Reference Frame (-3v)

🎳 Bowling Ball: Ball A

🏀 Basketball: Ball B

🎾 Tennis Ball: Ball C

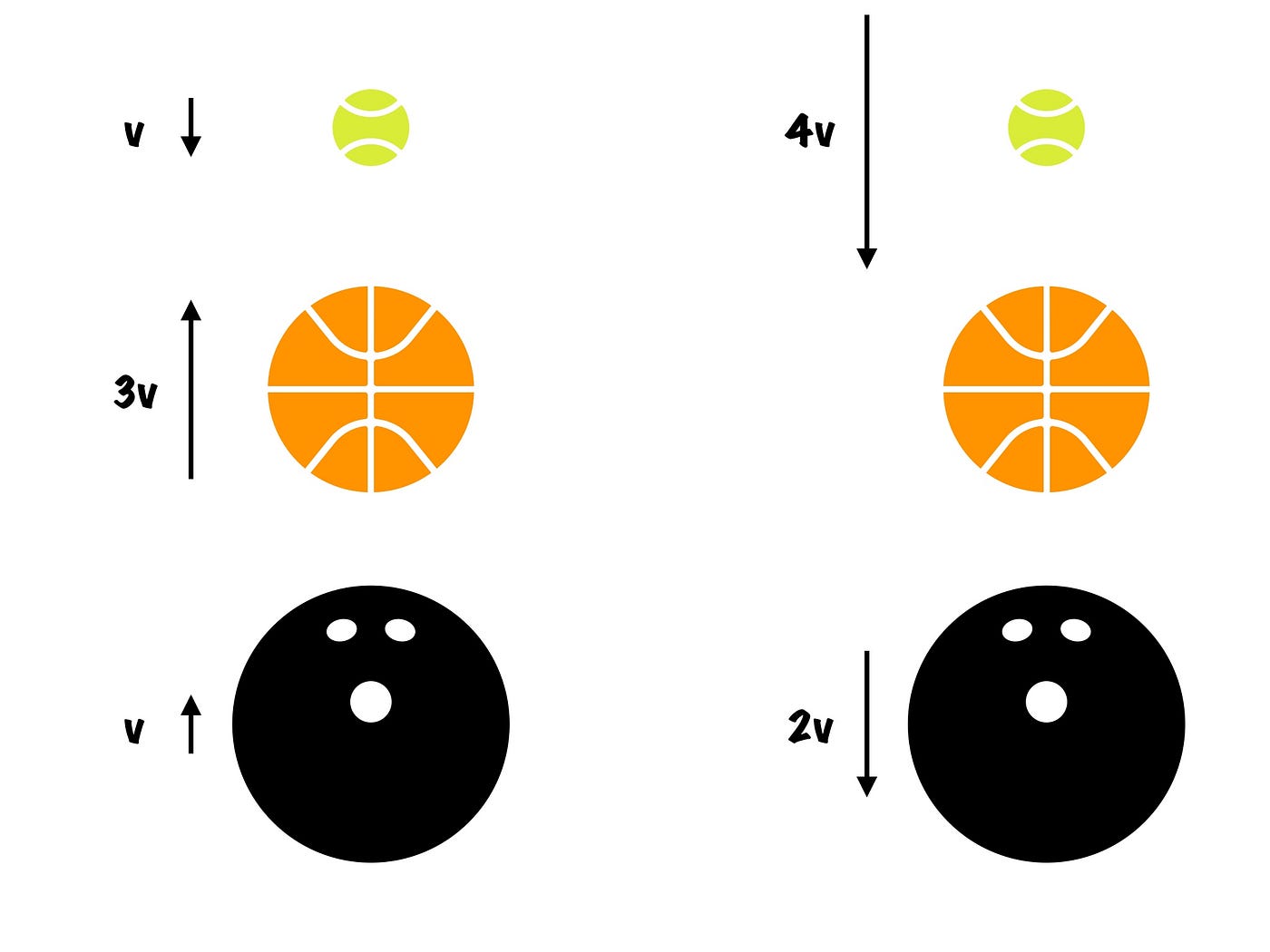
Calculations (collision of Ball B and C)

Back to observer’s reference frame (+3v)

Generalization

From this, we can already try to discern a pattern. Let’s get the common difference of our velocities.

Okay, this doesn’t reveal much. But if we extend our sequence and calculate the final velocity of the next few balls (which I encourage you to do yourself)…

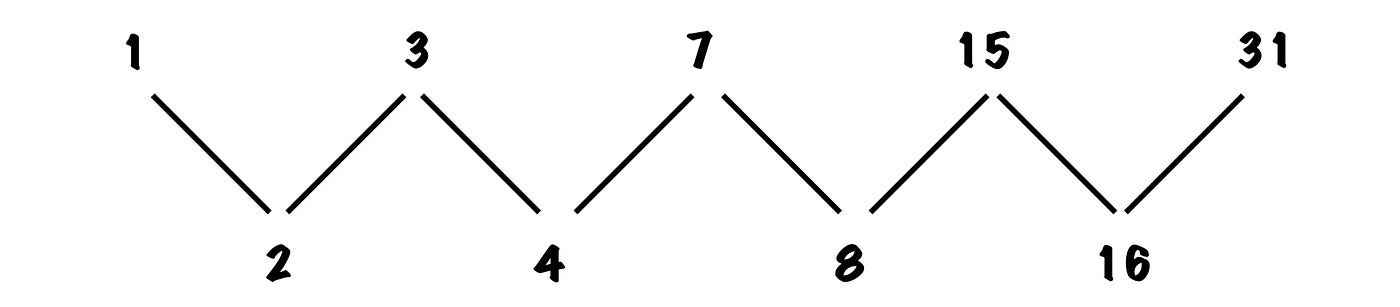
We can clearly see that the common differences are the powers of two! In other words, when stacking n balls and dropping them at a speed of v. The nth ball from the bottom will be the sum of the first n powers of two from 1 (or n=0). Mathematically this can be expressed as:

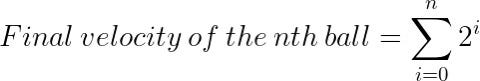
But instead of solving for the sum of the powers of two recursively, we can do so through the formula

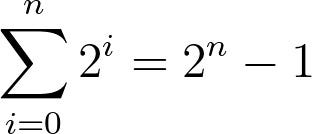
With this formula, we can calculate the speed if any amount of balls are stacked and dropped. Now let’s test that.

A not so practical example

One thing we can easily observe with the speed of the balls, is that the pattern grows rapidly. With say just four balls stacked and dropped, the fourth ball will bounce back at more than 10 times the initial speed!

But just to leave you all with a (not so) practical and a (much more) mind-tickling example, it’s time to think outside our planet. The escape velocity of the Earth (the velocity required to escape the Earth’s gravity) is approximately 11,000 meters per second. How many balls would we need to bounce to launch something out to space?

Using our formula, we know that the number of balls n to exceed 11,000 is

2 ⁿ - 1 > 11,000

2 ⁿ > 11,000

From here, we can use logarithms and get the smallest integer greater than the result

log ₂(11,000) ≈ 13.4

n = 14

And so all technicalities aside, it would just take bouncing 14 balls to escape the Earth’s gravity!

Mathematics is arguably the most intriguing when seen through the lens of practical applications, or physics as we have shown here. Physics in turn, is most enthralling when you take its practical applications to the limits. And when it comes to physics, the sky’s the limit, and beyond.