Comparing properties and patterns of the powers of two and the Fibonacci sequence

The Fibonacci sequence and the powers of two are quite possibly two of the most infamous patterns in and outside of mathematics. Both come from almost humble origins and beginnings, yet find extensive applications. The Fibonacci sequence and the golden ratio occur naturally in nature. Furthermore, they are used to create visually appealing designs — from 2-D artworks to 3-D structures. While the powers of two find use in computer science (binary code and bits) and graph theory (networks; more on that in a later article).

The nth Difference

Aside from their popularity, the powers of two and the Fibonacci sequence have other striking similarities. For instance, the differences between successive terms actually form the sequence they originated from.

Common Ratio

It is common knowledge the the powers of two is an example of a geometric sequence — with a common ratio of two. But strictly speaking, the Fibonacci sequence is not a geometric sequence, yet it somehow appears to behave like one. An example being how, like the powers of two, the Fibonacci sequence also tends to follow Benford’s Law. These uncanny similarities can be attributed to the golden ratio.

Golden Ratio

Given the following lengths

The ratio of b and a is said to be the Golden Ratio when a + b and b have the exact same ratio. Or algebraically

φ = b/a = (a+b)/b

This value can be approximated to φ ≈1.61803

Going back to the Fibonacci sequence, the ratios of consecutive terms appear to approach the Golden Ratio.

2/1 = 2

3/2 = 1.5

5/3 ≈ 1.667

8/5 = 1.6

13/8 = 1.625

…

With this, we can think of the Golden Ratio as an “almost common ratio” of the Fibonacci sequence, which is why it appears to posses some properties of geometric sequences. We can visualize how the ratios of Fibonacci numbers tend to the Golden Ratio with the following python program.

import matplotlib.pyplot as pltfib_ratio = []
fib_cache = {}def fib(n):
if n in fib_cache:
value = fib_cache[n]
return value
if n == 1:
return 1
if n == 2:
return 2
value = fib(n-2) + fib(n-1)
fib_cache[n] = value
return valuefor n in range(1,9):
num1 = fib(n)
num2 = fib(n+1)
ratio = num2 / num1
fib_ratio.append(ratio)plt.plot(range(1,9), fib_ratio, 'o', label='Ratios of consecutive Fibonacci numbers')x_coordinates = [0, 10]
y_coordinates = [1.61803, 1.61803]
plt.plot(x_coordinates, y_coordinates)plt.show()

Memoization algorithm above is courtesy of Michelangiolo Mazzeschi

Result:

‘Forcing’ The Fibonacci Sequence to be geometric¹

Using the more general definition of a Fibonacci sequence, we can construct a sequence that is geometric — common ratio and all. To do this, we can choose our first two terms to be 1 and the Golden Ratio φ. To generate the rest of the sequence, simply add the previous two terms like you would normally.

1 + (φ) + (φ + 1) + (2φ + 1) + (3φ + 2) + …

We can simplify this with the following property of φ:

φ = b/a= (a+b)/b
φ = b/a = a/b + 1
φ = 1/φ + 1
φ² = 1 + φ

Applying φ² = 1 + φ to our sequence, we get

1 + (φ) + (φ²) + (φ³) + (φ⁴) + …

And we see that the resulting sequence is geometric! Hence we have a general case of the Fibonacci sequence that is also a geometric sequence with a common ratio of φ.

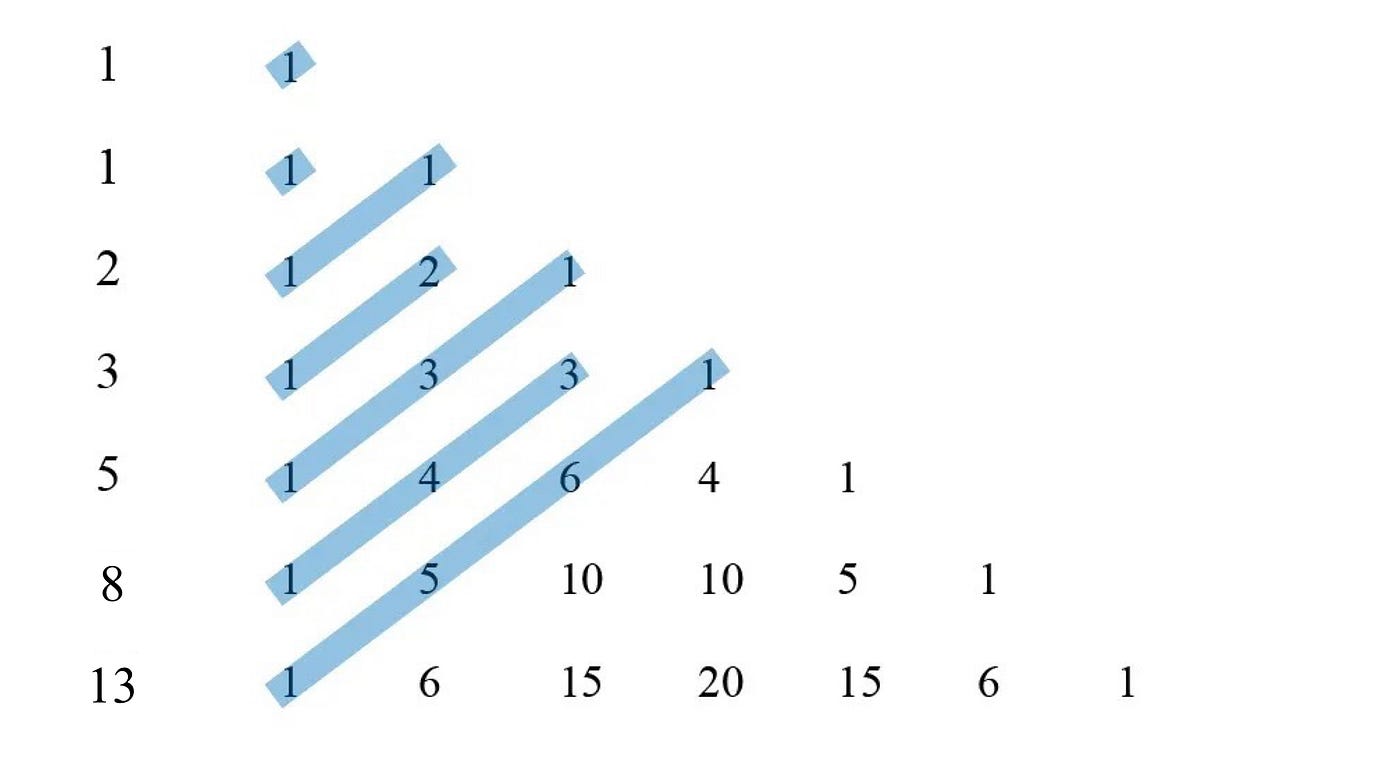
Pascal’s Triangle

Pascal’s triangle is formed by writing the sum of numbers beside each other below and in between them as follows:

The powers of two and the Fibonacci numbers are the sums of the rows and diagonals in Pascal’s triangle respectively. To see this, we can use a left aligned Pascal’s triangle².

Row Sums & Powers of Two³

The sum of all numbers in row n (from 0 onward) of Pascal’s triangle is equal to 2^n.

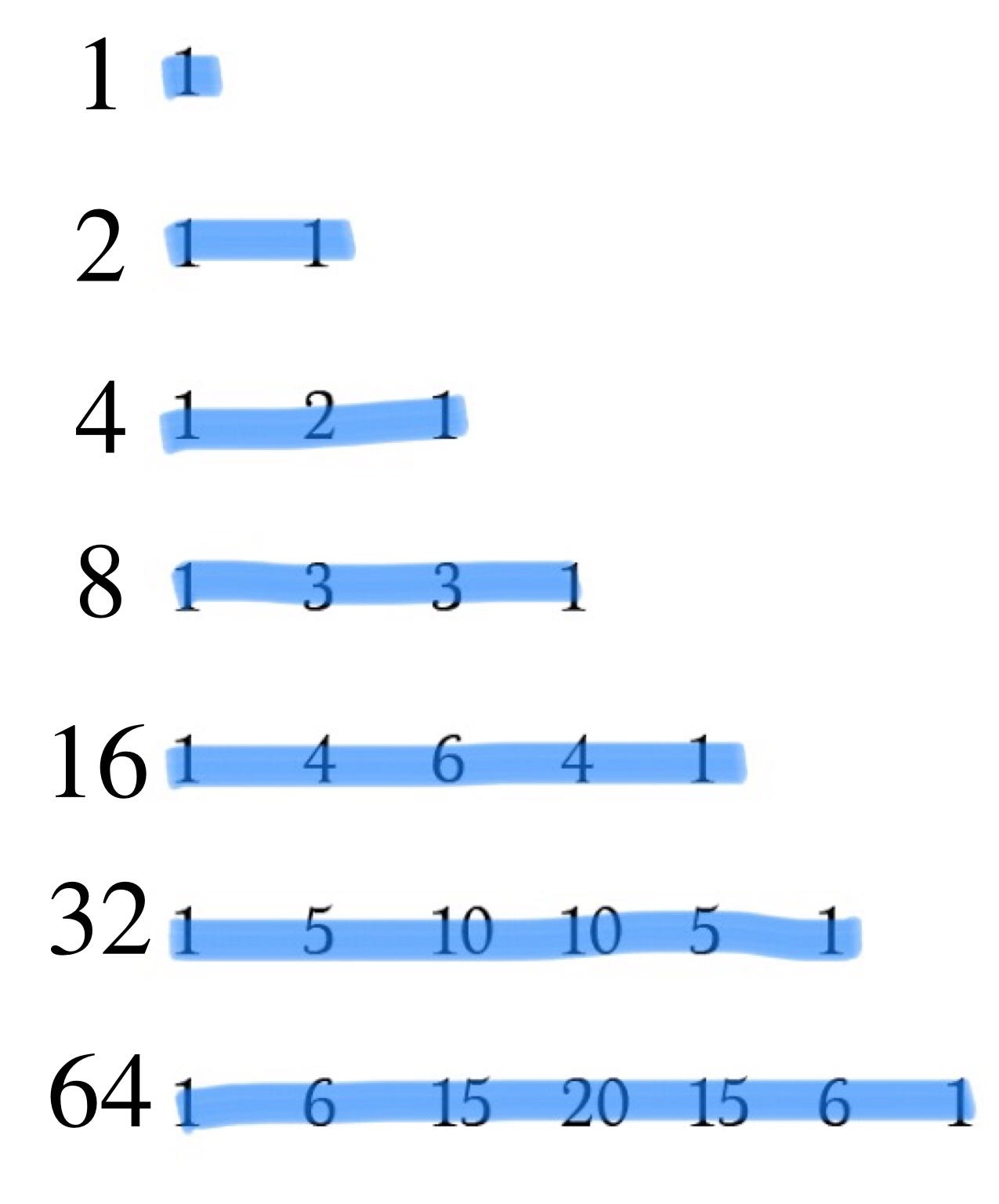
This is because the kth number on the nth row of Pascal’s triangle is C(n,k), therefore the sum of all terms in the nth row is

A proof can be made for the sum of binomial coefficients using induction or the binomial theorem, which can be found here.

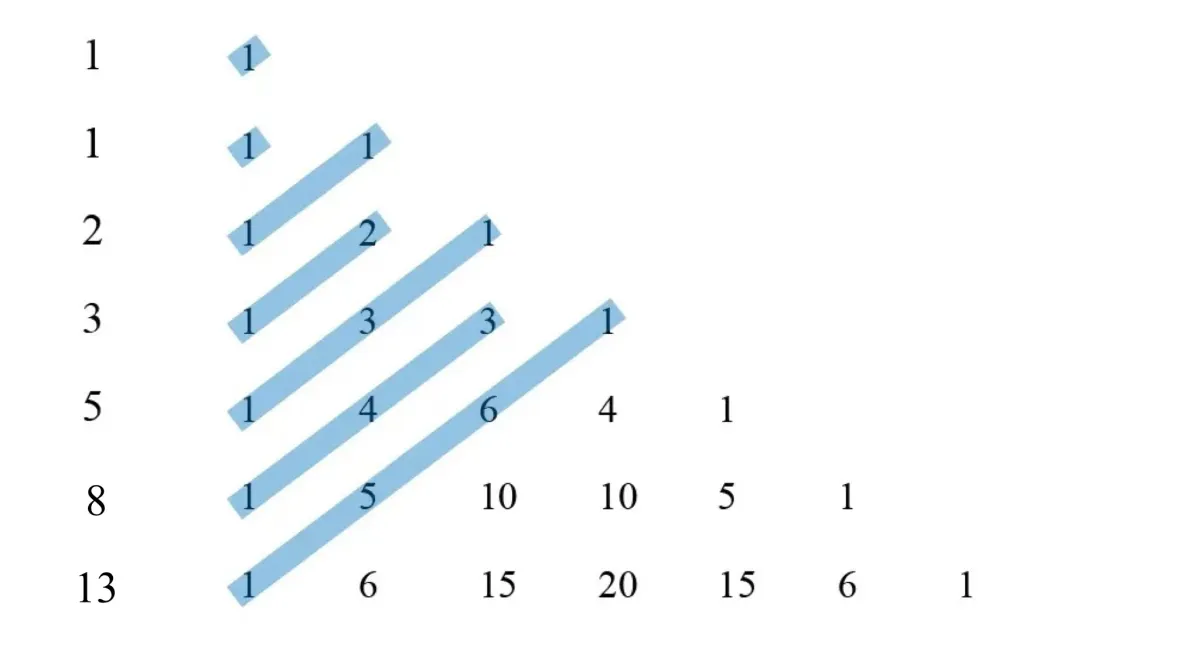
Diagonal Sums and Fibonacci Sequence⁴

The same applies for Fibonacci sequence, except this time we take the sum of diagonals.

The proof of this is beyond the scope of this article, but is discussed extensively in this paper.

“The Eight Conjecture”

What is the largest Fibonacci number that is also a power of two

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584

Given all their similarities, we would guess that there are many numbers that are both a power or two and Fibonacci. Yet at a glance, it seems like 8 could quite possibly be the largest power of two in the Fibonacci sequence. But then again, there might be more lurking farther down the list. When mathematicians aren’t completely sure of an assumption, they call it a conjecture. Here, we’ll make an “eight conjecture” and say that 8 is the largest Fibonacci number that is also a power of two. The challenge now is proving or disproving it.

To go about this, we will use the divisibility rule of Fibonacci numbers⁵.

This simply says that the greatest common denominator (GCD) of two Fibonacci numbers is another Fibonacci number with the GCD of their indices. Using this, here’s a quick proof⁶ by contradiction.

Let F[p]* be a power of two greater than 8. This implies

where | denotes divisibility. Hence with our formula we have

With this we can already tell that a power of two in the Fibonacci sequence should have an index that is a multiple of 6. But we can make further generalizations with m.

Given this, we can make the following statement

If F[6m] is a power of two, 
then F[m] is a power of two,
and gcd(F[m], 2) = 2,
or gcd(F[m], F₃) = F₃

Again, using the formula, we know that the gcd of the indices should be 3 as well, which means m is a multiple of 3. We can therefore express m as 3n, and substitute it back into F[6m] (we are nearly done).

However, this would mean F₉ = 34 also divides our supposed power of two:

Ergo, since F[p] has a factor of 34, and powers of two can only have factors that are other powers of two

*Instances of P[q] in this article refer to “P of q” or P with an index or a subscript of q.

Sources and Acknowledgements

Many thanks to Michelangiolo Mazzeschi for sharing his brilliant Memoization algorithm for the Fibonacci sequence.

[1] https://www.johndcook.com/blog/2009/05/11/fibonacci-geometric-series/
[2] https://medium.com/i-math/top-10-secrets-of-pascals-triangle-6012ba9c5e23
[3] https://proofwiki.org/wiki/Sum_of_Entries_in_Row_of_Pascal%27s_Triangle
[4] https://www.maplesoft.com/applications/view.aspx?SID=3617&view=html
[5] https://www.umflint.edu/sites/default/files/groups/Mathematics_Department/fielddaypdfs/teamessayproblems2008.pdf
[6] https://math.stackexchange.com/questions/795763/fibonacci-numbers-that-are-powers-of-2