Rainbows, who could remain untouched when run upon it? From ancient to nowadays times, it is an omen for an upcoming fortune, success, happiness, just positives, and no disasters. No surprise, though, because people feel good vibes during beautiful phenomena, they want to link them with heart-warming feelings. Some folk tales and legends go a step further and materialize it with a promise that a chest of gold, guarded by a gnome, waits at the end of the rainbow. Whether or not the chest of gold awaits for treasure hunters, rainbows will not stop please the eye.

I was an inquisitive child. I remember that I kept asking about everything without accepting the “it is the way it is” answer. I needed to know, or I could not sleep — fortunately, I am still like that. I can not get over the unknown. Oh, how many sleepless nights I had. In my childhood, whenever I heard “rainbow in the sky,” I was there faster than Usain Bolt was during 100 meters Olympic sprint. And I am sure all kids have and had alike.

Preliminary

What is then that causes a rainbow in the sky?

The secret lies in that white light is the superimposition of other colors and is dispersed if traveling among dispersible media. All colors creating white light have a slightly different frequency, which affects their speed in those media. Which in turn leads to varying angles of refraction. Thus, when passing through a medium, colors continually diverge from themselves, and when shot out of the medium, they appear as individuals.

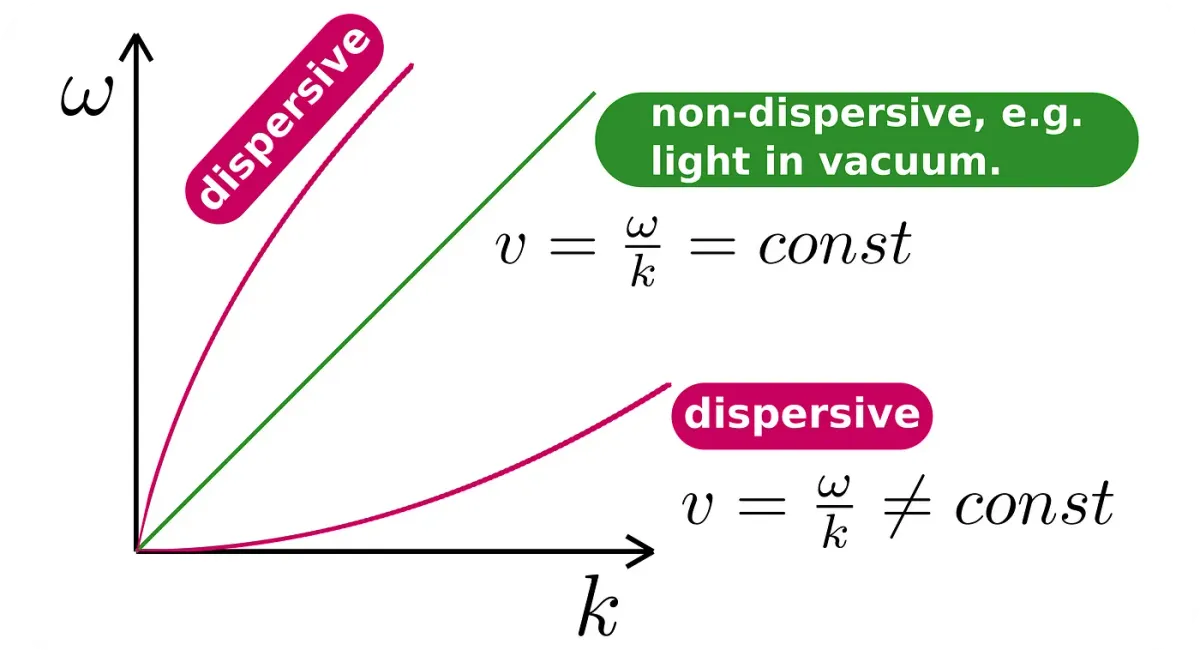
What does a dispersive medium mean?

It means that the phase velocity,

given by the ratio of ω (how many radians per second)

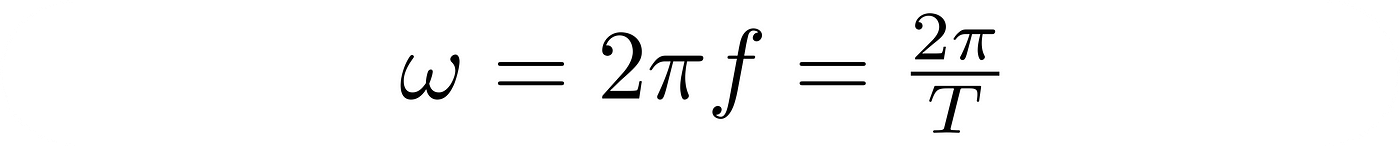
to k (how many waves per meter,)

varies among different frequencies.

That is all there is.

Snell’s law and angle, index of refraction

An optics tool used to describe the relationship between the angles of incidence and refraction, which are measured relative to the normal of separating them boundary; the boundary must separate two different isotropic media. It is a natural consequence of the fact that light travels according to the least time action. Mathematically speaking, it asserts that the ratio of sines of the angles corresponds to the velocities in these two media.

In other words, it tells how much light bends after it gets through the boundary.

It also tells that the incident light (if it is not total reflection) is reflected at the boundary at the same angle as the incident one.

Index of refraction is the ratio between the speed of light in a vacuum and any other medium.

For rainbows are bounded by violet and red color, it is reasonable to note their indexes.

Light and a water drop

The key to understanding the rainbow lies in dispersion, occurring when sunlight hits a single water drop.

Consider the picture below and the sunray that hits the water drop at point A.

At that point, some of the light gets reflected; whereby, the rest continues its motion to point B, during which constituted colors diverge from themselves. Finally, this portion of the light hits the water drop at B.

Is there any reason to study the light that leaves the water drop here?

— No, because rainbows are observable when looking away from the Sun.

Therefore, following the light leads to C. As this light is observable when looking away from the Sun, it is worth analyzing.

Every proof requires quantity(ies) that generalize the problem to all cases. In this problem, it is γ, which tells the span of angles at which rays can leave the water drop at point C.

Calculating γ

The δ and ε angles of the triangle CDE from the picture above are crucial to finding γ; getting them gives the γ.

Let’s figure them out by filling all angles above with their values.

So, δ is the same as α, whereby ε is

Which gives γ equal to

Thus, knowing the incident(α) and refraction(β) angles allows determining at what angle the rays leave the water drop. That is a huge step forward.

Calculating the derivative of γ with respect to α and checking when it equals zero

Why a derivative at all?

Because it allows determining all stationary points of a function for which being calculated: minima, maxima.

Why with respect to α?

Because α is the angle of incident, it tells what path light takes in the water drop, relative to its entry point. Moreover, β depends on α.

So

From Snell’s law

Plugging it back

Continuing

Finally

Now, plugging into this equation indexes of refraction of red and violet light reveals incident angles at which γ have a maximum. But, to calculate γ, β must be estimated first. Then both, α and β, can be plugged into the γ equation.

Summary

The results mean that each color creates a separate cone of light in a span between 0° and its γ max.

The last unknown

One mystery remains unsolved, namely, if each color can leave the water drop at any angle ranging up to its γ max, then why they do not overlap with each other, creating some mixture of colors with dominating white light?

Because of varying intensities of colors, what the human brain perceives as a color is an excess of one over all others. In a diagram, it looks roughly like the below one.

Formation of a rainbow

From a single water drop to a rainbow does not lead long road. A missing part is how water drops work together when forming one.

Imagine water suspended in the air. Dozens of molecules are hit continuously by sunlight. In each of them, sunlight is reflected and refracted, as was shown. Thus, if you direct your head away from the Sun at 42.4°, you will see the red light. But, this, and any other color does not come from one molecule but all at an adequate angle. It means that when an observer is on the ground, molecules returning a given color(as seen by the observer) aligns in a bow shape. Hence, the overall effect is the collective work of all water drops.