Abel

The Mozart of Mathematics — Niels Henrik Abel

“Although Abel shared with many mathematicians a complete lack of musical talent, I will not sound absurd if I compare his kind of…

Jørgen Veisdal

— 23 min read
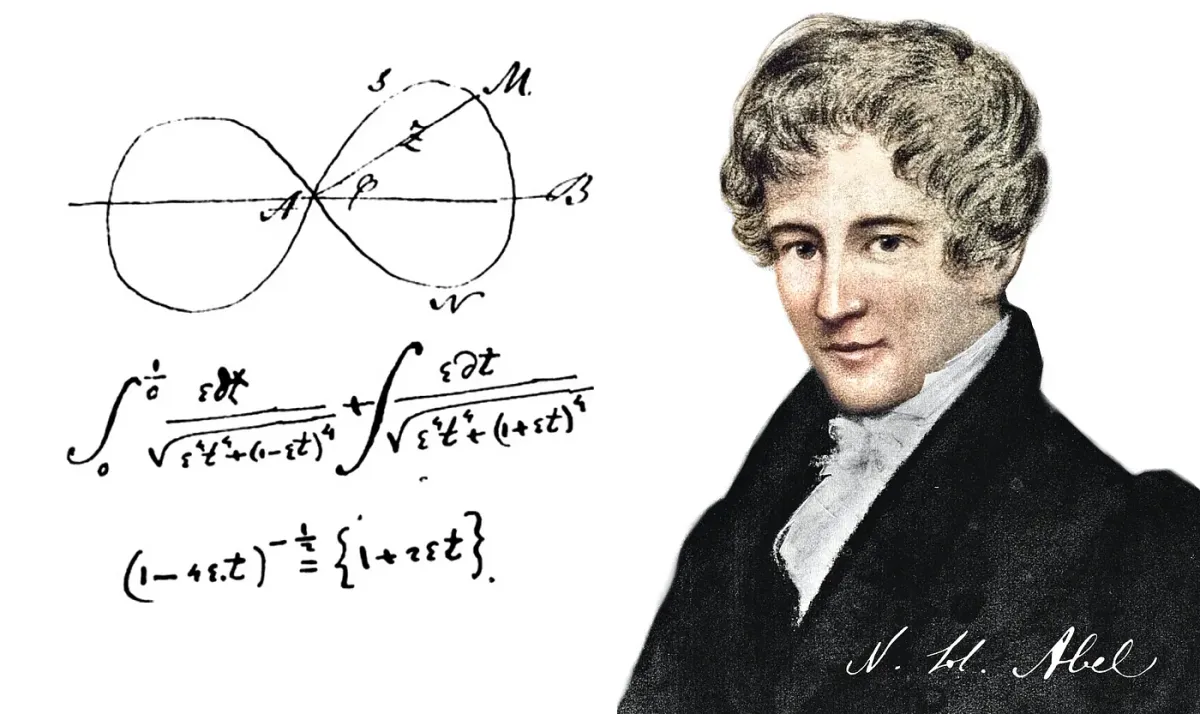
The Mozart of Mathematics — Niels Henrik Abel
Left: A doodle from one of Abel’s notebooks. Right: The only known portrait of Abel, by Norwegian painter Johan Gørbitz (1826, edited and colorized)
“Although Abel shared with many mathematicians a complete lack of musical talent, I will not sound absurd if I compare his kind of productivity and his personality with Mozart’s.” — Felix Klein

Niels Henrik Abel (1802–1829) died at age 26. Largely self-taught, during his short life the young Abel made pioneering contributions to variety of subjects in pure mathematics, including: algebraic equations, elliptic functions, elliptic integrals, functional equations, integral transforms and series representations. Born on the small island of Finnøy in Rogaland, Norway, the early years of Abel’s short life was dominated by the instability of an alcoholic father who died when he was 16 years old.

More or less self-taught, at 21, Abel provided the first complete proof demonstrating that there is no general algebraic solution for the roots of a quintic equation, or any general polynomial equation of degree greater than four. At that point, the problem had been unresolved for over 250 years. In the process of writing the proof, he laid the foundation — independently of Galois — for the branch of mathematics now known as group theory. At 22, he also wrote a fundamental work on elliptic integrals which helped lay the foundation for what would later be the theory of elliptic functions. Then, on April 6th 1829, at the age of 26, Abel died of tuberculosis. He had contracted the disease while in Paris and gotten ill while travelling by sled to the south of Norway in December to visit his fiancée.

Unbelievably, for the duration of his brief life he was never able to attain a permanent research or teaching position. Living hand-to-mouth from scholarships, temporary teaching positions and various patrons, at the time of his death he was working to repay the debts of his family in abject poverty. In the ultimate cruel irony, not two days after he passed a letter arrived from August Crelle (1780–1855) (of Crelle’s Journal) announcing that had been appointed Professor at the University of Berlin.

This is the story of Niels Henrik Abel, the Mozart of Mathematics. Estimated reading time is 30 minutes. For the occasion, recommended mood music is Requiem, K. 626: Lacrimosa, available on Spotify or YouTube.

Early Life (1802–1821)

Niels Henrik Abel was either born on the island of Finnøy or in Nedstrand near Stavanger in Denmark-Norway on August 5th 1802. His father Søren Georg Abel was a pastor at the local church on Finnøy, as was his father Hans Mathias before him. Their family originated from Denmark. His mother Anne Marie Abel (born Simonsen) was the daughter of a wealthy shipping merchant. Niels Henrik had one older brother (Hans Mathias), three younger brothers (Thomas Hammond, Peder Tuxen and Thor Henrik) and a younger sister (Elisabeth). Their father Søren had earned a degree in theology and philosophy in Bergen, and was appointed pastor at Gjerstad Church in Risør when Abel’s grandfather Hans Mathias died. The family moved there in 1804.

Gjerstad Church where Abel’s father Søren was a pastor (1890)

When Norway adopted its first Constitution ten years later, in 1814, Abel’s father Søren became a member of Parliament in Oslo (then Christiania). He held the seat until 1818, when his political career abruptly ended after he was almost impeached for making unfounded accusations against a cabinet member from the podium of the parliament. Sick and worn down, Søren returned to Gjerstad in 1818. An alcoholic, he died two years later at a mere 48 years old.

Christiania Cathedral School (1815–1821)

Drawing by Anna Diriks (1882) depicting the corner of Dronningensgate and Tolbodgaten with Christiania Cathedral School visible on the right (Photo: Wikimedia Commons)

Although he was home schooled at first, at 13 years old Abel left home to join his older brother Hans at Christiania Cathedral School in Christiania (now Oslo). The formal requirements for admission to the school were

  1. Be at least ten years of age
  2. Be able to demonstrate insight into history and geography
  3. Proficiency to read Danish and Latin, and
  4. Be acquainted with the four species of mathematics

Despite his rural upbringing, Abel qualified and left for the capital in 1815. His father Søren helped him find housing with a merchant. His quarters included a small room with a bed, table, stool and (perhaps) a window overlooking a stable yard where horses and wagons came and went with packing crates and other goods (Stubhaug, 1996). With the considerable time required for travel (by horse and buggy or sled, depending on the time of year), Niels Henrik likely did not return home to see his family for the duration of his first and second year in Christiania. He was fourteen years old.

Being a disciple at the Cathedral School was a full-time occupation. School began at nine o'clock with four hours of morning lessons, and as a rule, three hours in the late afternoon. The day ended at six in the evening. In addition there was homework and preparation, day in and day out, six days a week without variation.- Excerpt, "Niels Henrik Abel and his Times: Called Too Soon by Flames Afar*" by Stubhaug (1996)

As his posthumous biographer Arild Stubhaug writes — somewhat fortunately for the burgeoning mathematical protege — more than half of Abel’s 40 hour school week as a teenager was devoted to languages. These included lessons in Danish as well as in modern foreign languages such as German and French, and of course Latin. A proficiency in such languages was no doubt crucial for any aspiring scientist of the age, as the lingua franca of mathematics at the time was a mixture of French and German.

The Lecture Hall at Christiania Cathedral School prior to 1823 (photo from Stubhaug, 1996 pp. 154)

Somewhat surprisingly, Abel did not fall in love with mathematics immediately. Indeed, he paid no special attention to the subject until he had attended the Cathedral School for nearly three years, in 1818. This because, for the first three years there his mathematics instructions “did not venture much beyond the demand that the pupils copy things down from the blackboard“ (Stubhaug, 1996).

There were, of course, no textbooks at the time. Indeed, had there been textbooks, Abel would not have been able to afford them. Writing home to his superior in Gjesdal, his father Søren reported in 1818 that the tuition at his son’s school was 90 speciedaler per year (about $450), which with the addition of costs for books and clothes meant that “There is nothing left but Milk and Gruel, Gruel and Milk for my remaining family” (Stubhaug, 1996). He ended his letter:

“I will pay with the Shirt off my back. My children are my All” — Søren Abel

By 1818 however, a new, twenty-three year old teacher by the name of Bernt Michael Holmboe (1795–1850) had assumed the teaching of mathematics at Abel’s school, which would change the 16-year-olds’ life forever.

Inspired by the self-taught Joseph-Louis Lagrange (1736–1813), Holmboe was cautious about claiming to know the best way for students to learn, instead emphasizing that his students read the works of Euler (which Holmboe’s hero Lagrange had done) and adhere to the following principles (adapted one of Lagrange’s papers, published in Zeitschrift für Astronomie und verwandte Wissenschaften):

How to study mathematics, according to Abel's high school teacher1. Never study more than one book at a time and never abandon a book you have chosen without working all the way through it2. If you face difficulties, do not give up but instead go back twenty times if that should prove necessary and only then allow yourself to investigate another mathematician's solution3. Skip over those parts that are of no challenge in order to get at what is new to you4. Reflect over the reading, in particularly how the writer came to the solution and moreover, what the solution leads to5. Investigate whether or not another transformation or substitution would have solved it in a better manner6. Always read with pen in hand so that you can work out all the calculations and practice all the questions you encounter7. Write up lists of subjects that afford you an opportunity to develop your own theories8. Geometric reflections can be a suitable way of strengthening and securing one's judgement

As Stubhaug writes, in 1818 Abel “could hardly prove that there were infinitely many prime numbers”. By 1819 however, inspired by his new teacher, Abel had rapidly completed the required instruction in elementary mathematics. At 17 years old, he moved on to receive private lessons in higher mathematics from Holmboe, who helped him through the classics of Euler, Poisson and of course, his tutor’s idol Lagrange (Stubhaug, 1996). Before long, “Holmboe unashamedly boasted about his disciple, and with the conclusion of the school year in the summer of 1819, he wrote in the school register about Niels Henrik” :

“A splendid mathematical genius”

Reportedly, not more than a year later, at the time of Abel’s graduation in 1820, Holmboe had run out of things to teach him as Abel had already ventured on and studied all the latest mathematical literature in the Royal Frederick University library. As his posthumous autobiographer Stubhaug later wrote:

“By 18, Abel was likely the most knowledgeable mathematician in Norway”

University (1821–1822)

Abel entered the Royal Frederick University (now the University of Oslo) in 1821 on a scholarship raised for him by his patron and teacher Holmboe and his friends. He remained there for less than a year before graduating with a Bachelor of Arts degree in mathematics in 1822. His report card included “exceptionally high” marks in mathematics and mediocre grades in everything else.

Following his graduation, without any prospects for work or other income, Abel was on the verge of homelessness until he was taken in by his former professor — the leading natural scientist in Norway at the time — Christopher Hansteen(1784–1873) and his wife Johanne Borch Hansteen. Abel would later refer to Johanne as his “second mother”. Indeed, she “seems to have been the person who gained the deepest glimpse into Niels Henrik’s feelings and sensibilities” (Stubhaug, 1996). The Hansteens in other words provided for the young Abel, who had lost his father and whose mother lived in rural Norway and knew nothing about the life in the capital. In addition to providing him with a place to live and food, Hansteen also did his best to promote Abel’s name in the European mathematical community.

Abel’s two most important patrons. Left: Adjunct Bernt Michael Holmboe. Right: Professor Christopher Hansteen.

Indeed, throughout his brief life, the “unsophisticated” Abel was helped by many friends and patrons who — although most did not grasp the importance or implications of his work — supported his aspiring mathematical career. In addition to Holmboe and Hansteen, the following in particular stand out:

  • The “other” Professor of Mathematics at the University of Christiania (now the University of Oslo), Søren Rasmussen (1768–1850) who in 1823 gave Abel a gift of 100 speciedaler (about $580) so that he could travel to Copenhagen to visit mathematician Carl Ferdinand Degen (1766–1825).
  • Abel’s principal at Christiania Cathedral School, Niels Treschow (1751–1833), without whom’s considerable effort in shaping school policy, Abel most likely would not have been exposed to Holmboe. When Abel applied for a two-year travel grant of 600 speciedaler (about $5500) in 1825, Treschow supported his request. When he returned from abroad, he stayed in Treschow’s home which also served as his sister Elisabeth’s home and place of work for years.
  • The Professor and Doctor Michael Skjelderup (1769–1852) who let Abel live in his home when he needed it.

Career (1821–1829)

Abel’s professional research career began when he published his first proofs in the newly founded Magazin for Naturvitenskaberne (“Journal of Natural Scientists”) in 1823. Abel’s first work to be published in a journal was:

The paper regarded functional equations. In particular, Abel considered a very general type of functional equation (Houzel, 2002):

Where φ, f, F, … are unknown functions of one variable and α, β, γ, . . . are known functions of independent variables x and y. His investigation was in a method of eliminating the unknown equations of one variable until he could arrive at a differential equation with only one unknown function and one variable. In the paper he used the method to derive functional equations for various classical equations from mechanics and physics.

Following his first publication, Abel also wrote a French paper (likely) titled:

  • Abel, N. H. (1823). Une représentation générale de la possibilité d’intégrer toutes les formules différentielles (“A General Representation of the Possibility to Integrate all Differential Formulas”)

He applied to the Royal Frederick University for funds to publish it, but despite the support of his patrons Professor Rasmussen and Hansteen, the committee did not immediately approve the grant and the paper was forever lost.

Abel’s second journal paper was however published in the same issue of Magazin for Naturvitenskaberne (“Journal of Natural Scientists”) as his first:

The paper regarded integral transforms and likely contains the first case of an integral equation (an equation in which an unknown function appears under the integral sign) in the history of mathematics. As Houzel (2002) writes:

“Before that, Euler had introduced in his Institutiones Calculi Integralis the general idea to solve a differential equation by a definite integral, for instance by the so called Laplace transform and Fourier (1811) and Cauchy (1817) had studied the Fourier transform and its law of inversion.”

In the paper, Abel first studied the integral equation

where ψ is a given function and s is an unknown function of variables x and n < 1. Abel next investigated the particular case where n = 1/2 by developing s as a power series and using the Euler function Γ, citing Adrien-Marie Legendre(1752–1833). He later published a version of the same study in German in “Crelle’s Journal”, the Journal für die reine und angewandte Mathematik in 1826. In the second part of the 1823 paper, he also proved and the integral formula

The Quintic Equation (1824)

In the spring of 1824, following the publication of his first two journal papers Abel’s fortunes were finally looking up. He was granted a scholarship for 200 speciedaler (about $1500) for the next two years and a promise for an additional 600 speciedaler for two years of travel after that.

His most well-known result came around the same time, when wrote a booklet in French demonstrating (with proof) why it is impossible to solve the general quintic equation by radicals:

The general quintic equation is of the form:

As the story goes, already in 1821 Abel believed that he had discovered a method of solving the equation before realizing that there was an error in his solution, which he later employed to prove that any such solution is impossible. He first showed his (unbeknownst to him, faulty) solution to professors Rasmussen and Hansteen, neither of whom found any errors. They next forwarded the solution to the leading mathematician in the Nordic countries, Carl Ferdinand Degen(1766–1825) who also did not find any mistakes but still doubted the solution, noting however that

“[The work] exhibits, even if the Goal has not been proven, an uncommon Mind, and uncommon Insights, particularly for his Age.” — Degen, 1821

Although he hesitated to forward the solution in its current form to the Royal Academy of the Sciences, Degen suggested Abel send a more detailed treatment and a numerical example, to strengthen his argument.

What Abel surely didn’t know at the time, was that a supposed proof of the impossibility of solving quintic equations had already been published by an Italian mathematician named Paulo Ruffini (1765–1822) in 1799, 1802 and 1813. Ruffini’s proofs were however incomplete, because he had supposed (without proof) that the radicals of a hypothetical solution were rational functions of the roots (Houzel, 2002). Abel’s proof (which he came to after failing to provide a numerical example to Degen) indeed begins with a proof of this supposition, namely that the root of the equation:

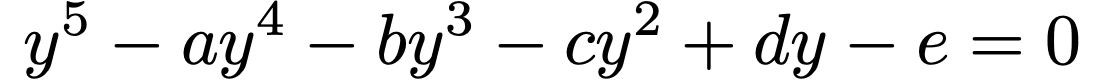
is of the form

In the interest of completeness, Abel’s proof of the impossibility of solving the quintic equation in radicals, in its entirety, is provided below:

Although due to financial reasons it is likely that very few copies of the paper were sold, Abel sent quite a few copies around to colleagues and through Hansteen, to Heinrich Christian Schumacher (1780–1850) in Hamburg, who showed the paper to Carl Friedrich Gauss (1777–1855) in July 1824 (Stubhaug, 1996). Reportedly, Gauss’ initial reaction was negative, as he believed he could prove the opposite. However, as time moved on, Gauss too came to believe Abel’s proof to be correct.

A Failed Attempt at Applied Mathematics (1824)

Abel’s sole effort in applied mathematics was his 1824 paper:

At the encouragement of Professor Hansteen, as the story goes, Abel was given the task of calculating the moon’s gravitational pull using a pendulum on which a measuring apparatus was attached. As he was the editor of Magazin for Naturvidenskaberne, Hansteen published Abel’s paper reporting his findings during the spring of 1824. Hoping that the result would serve as Abel’s introduction to the academic circles of Europe, Hansteen even sent it to Schumacher who served as the editor of Astronomische Nachrichten. As it turned out, Abel’s calculations of the gravitational pull of the moon were very wrong (about six orders of magnitude) and so Schumacher refused to publish the paper. Worried that he might mention the blunder to his friend Gauss, Abel was embarrassed and never again ventured into topics outside of pure mathematics.

Integral Equations (1825)

Abel’s fourth article published in the Norwegian journal Magazin for Natuvidenskaberne appeared the following year:

Building on the findings of his second article in the same journal two years prior, the his 1825 paper too regarded integral equations, in particular a derivation and extension of the formula:

Derivations of the formula had already been published five years earlier by Giovanni Antonio Amadeo Plana (1781–1864) in Memoirs of the Turin Academy(Houzel, 2002), but Abel was likely unaware of this fact. It would not be until 1848 before Schaar established the result rigorously based on Cauchy’s residue theorem (Houzel, 2002).

European Tour (1825–26)

The summer of 1825, Abel set out on a European tour with four other young Norwegian scientists. With him, Abel had geologists Balthazar Mathias Keilhau(1797–1858), Nikolaj Benjamin Møller (1802–1860, Nils Otto Tank (1800–1864) as well as doctor/veterinarian Christian Peter Boeck (1798–1877). Abel was intending to visit the mathematical centers in Göttingen and Paris. Most notably, on the faculty of the University of Göttingen at the time was Gauss, the most prolific mathematician of the day and Euler’s most important descendent. Famously, Abel once wrote of Gauss’ style

“He is like the fox, who effaces his tracks in the sand with his tail.”

To which Gauss is reported to have once replied “No self respecting architect leaves the scaffolding in place after completing his building.” Despite his plans, while in Copenhagen Abel was convinced by his fellow travelers to instead come with them to Berlin. There, he met August Crelle for the first time (of “Crelle’s Journal”, where Abel would later publish) who introduced him to Berlin’s mathematical milieu. Following a successful stay from October 1825 to March 1826, the young Norwegians continued on to Dresden (where he met the Norwegian painter Johan Christian Dahl), Prague, Vienna, Graz and Trieste. About his aborted previous plan to visit Gauss in Göttingen, Abel later stated that he had chosen to instead follow along with his friends in order to avoid growing homesick. Indeed, homesickness may have been an issue for Abel during his travels, as he in a letter dated January 1826 wrote to Holmboe:

Excerpt, Letter from Abel to Holmboe (Berlin, 1826)[...]I wish I were home, which I miss terribly. Write me now at least a long Letter, telling me Every kind of Thing. Sit down and do this as soon as You get my Letter. Tomorrow I am going to the Comedy theatre to see Die schöne Müllerinn. Goodbye, and greet my Friends and Acquaintances.Your Friend, N. H. Abel

Having made the acquaintance of August Crelle, Abel wrote and submitted three papers to his newly established journal. The first was published as:

In the paper, Abel gives a general and (almost) rigorous proof of Newton’s binomial formula (Houzel, 2002):

Employing ideas by Euler, Cauchy and Lagrange Abel goes on to (almost) show continuity for the sum of the series of continued fractions.

Memorial plaque on the facade of the apartment building Abel lived in at Am Kupfergraben 4a in Berlin (Photo: International Mathematical Union, 2014)

Elliptic Functions (1826–29)

When Abel in 1821 believed he had found a solution to the quintic equation, the Danish Professor Carl Ferdinand Degen who reviewed his proof added the following comment in his review letter:

Excerpt, Letter from Carl Ferdinand Degen to Abel (1821)
I can scarcely repress the Wish, that the Time and the Mental Powers of the Head which Mr. A. blesses us with, not be utilized, from my Perspective, on sterile Subject Matter, but ought rather be applied to a Theme, whose Edification would have the most important Consequences for the whole Analysis and its Application to dynamic Explorations:I am thinking of the elliptical transcendents.With the proper Approach to Investigations of this Type, serious Scrutiny by no means becomes static, nor do the highest and more remarkable Functions, with their many and handsome Properties, become something in and for themselves, but rather, it is going to reveal the Magellan-Voyages to great Regions of one and the same immense analytic Ocean.

By elliptical transcendents, Degen was referring to what was has later been named elliptical functions and integrals. Abel’s first contribution to the theory came while he was in Paris, through the publication of the paper:

This paper (in addition to two more, which he wrote in Berlin), as Houzel (2002) writes, grants Abel claim to the title of “the founder of the theory of elliptic functions”. The most important work appeared in Abel’s last two papers published while he was still alive, both in Crelle’s Journal, in its second- (1827) and fourth volume (1829).

  • Abel, N. H. (1827). Recherches sur les fonctions elliptiques (“Research on Elliptic Functions”). Journal für die reine und angevandte Mathematik 2, pp. 101–181.
  • Abel, N. H. (1829). Précis d’une théorie des fonctions elliptiques (“A Precise Theory of Elliptic Functions”). Journal für die reine und angevandte Mathematik 4, pp. 309–348.

In the first paper, Abel sets out by recalling the main results of Euler, Lagrange and Legendre on elliptic integrals and defines the function φα = x by the relation

where c and e are real numbers. In the second paper, Abel describes a method for expressing elliptic functions as quotients of functions of a similar type as Weierstrass functions (named after Karl Weierstrass, 1815–1897).

Abel did write another paper while he was still in Paris (which was presented to Augustin-Louis Cauchy (1789–1857) in October of the same year, who described it as “a monument more lasting than bronze”). However, the paper was lost by the French Academy of Sciences until 1841, when it was finally published as:

  • Abel, N. H. (1841). Mémoire sur une Propriété Générale d’une Classe Trés Étendue de Fonctions Transcendantes (“Dissertation on a General Property of a Very Extended Class of Transcendent Functions”). Mémoires présentés par divers savants à l’Académie Royale des Sciences de l’Institut de France, t.VII. pp. 176–264.

The oeuvre of Abel’s work on elliptic functions is available here.

Contributions to Mathematics

“No one in Norway had sufficient mathematical knowledge to understand the significance of his stringent proofs”

Abel’s working career was remarkably short, lasting a mere seven years from his entering university in 1821 to his death in 1829. Although he in his short life published nine journal papers, most of his work remained unpublished until his collected works were gathered by fellow Norwegian mathematicians Peter Ludwig M. Sylow (1832–1918) and Sophus Lie (1842–1899) and published in two volumes under the title:

Modern editions of this work is available on Amazon (Affiliate Link). Among the most important findings of career, it is worth mentioning:

Abel’s Differential Equation Identity

In Abel’s 1829 paper in the Journal für die reine und angevandte Mathematik, he presented an equation that expresses the Wronskian determinant of two solutions of a homogeneous second-order linear ordinary differential equation in terms of a coefficient of the original differential equation.

Algebraic Solutions to Higher Order Polynomials

Abel’s proof of the impossibility of solving polynomials of higher orders than four is now known as the Abel-Ruffini theorem for its two main contributors, Abel and Ruffini (1765–1822).

Abelian Integrals

However famous Abel’s result about the impossibility of solving quintic equations, the most famous of his results among mathematicians likely still remains his extension of the Euler addition theorem for elliptic integrals, now known as Abelian integrals.

The Invention of Group Theory

In proving that there are no general algebraic solutions for the roots of quintic equations, Abel invented (independently of Galois) what later became known as group theory. In addition to Galois, the topic was also studied in the same period by Joseph-Louis Lagrange (1736–1813).

Definition of Abelian groups
An Abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written.That is, a group is Abelian if xy = yx for any two of its elements.

Elliptic Functions

Definition of Abel elliptic functions
Abel elliptic functions are holomorphic functions of one complex variable with two periods.

Abel’s elliptic functions are a generalization of trigonometric functions. Specifically, they are inverse functions of elliptic integrals, Abel’s definition was the first establishment of the elliptic functions which were shortly thereafter defined by Carl Gustav Jacobi (1804–1851). Abel, in other words, defined elliptic functions before Jacobi, but the latter’s definition later became the standard. For completeness, Jacobi elliptic functions are defined as:

Definition of Jacobi elliptic functions
Jacobi elliptic functions are meromorphic functions of one complex variable with two periods.

Abelian Functions

Definition of Abelian functions
An abelian function is a meromorphic function on an abelian variety, which may be regarded therefore as a periodic function of n complex variables, having 2n independent periods; equivalently, it is a function in the function field of an abelian variety

In addition to these, Wikipedia lists the following namesake contributions as among Abel’s most important:

Death and Legacy

Abel’s former professor and patron Søren Rasmussen stepped down from his professorship in 1825, leaving a vacant position. No doubt, despite the fact that Abel was traveling Europe at the time, he was nominated by Professor Hansteen. In the end, two candidates were seriously considered for the position: Abel and his former mentor Holmboe. In December of the same year, Holmboe was awarded the position, primarily because Abel was considered “still young, and perhaps yet unable to teach elementary mathematics in an suitable manner”.

Final Years (1827–29)

Abel returned from Paris in January 1827. While there, he had contracted tuberculosis. On his return back, he stopped in Berlin where he was offered a position as editor of Crelle’s Journal, which he turned down. He returned to Christiania in May of the same year. Despite his initial success in Berlin, he had not published in Paris and so was not able to secure an academic appointment. As such, he remained in poverty for the remainder of his life.

Abel had met the (only known) love of his life, Christine Kemp at a ballroom dance on the marine base Christianshavn in 1823. As the story goes, the two danced the new dance “the waltz” even though neither of them knew the steps. They got engaged during Christmas of the following year, in 1824. Having come back from his travels abroad, also during Christmas four years later, Abel traveled by sled to Froland where Christine was living. He became seriously ill on the journey and despite a brief improvement died in April of 1828 at age 26.

Two days after his death, a letter arrived from August Crelle in Paris announcing that he had managed to get him appointed as a Professor at the University of Berlin on the merits of his publications in Crelle’s Journal.

Legacy

Although largely unappreciated in his home country during his lifetime, Niels Henrik Abel is today widely considered to be the greatest Norwegian mathematician who has ever lived. Growing up in rural Norway at a time when the country was a poor and uneducated, his brief but brilliant rise to prominence in the mathematical milieu of Paris and Berlin remains nothing short of unprecedented in a country of less than 6 million people as of 2020.

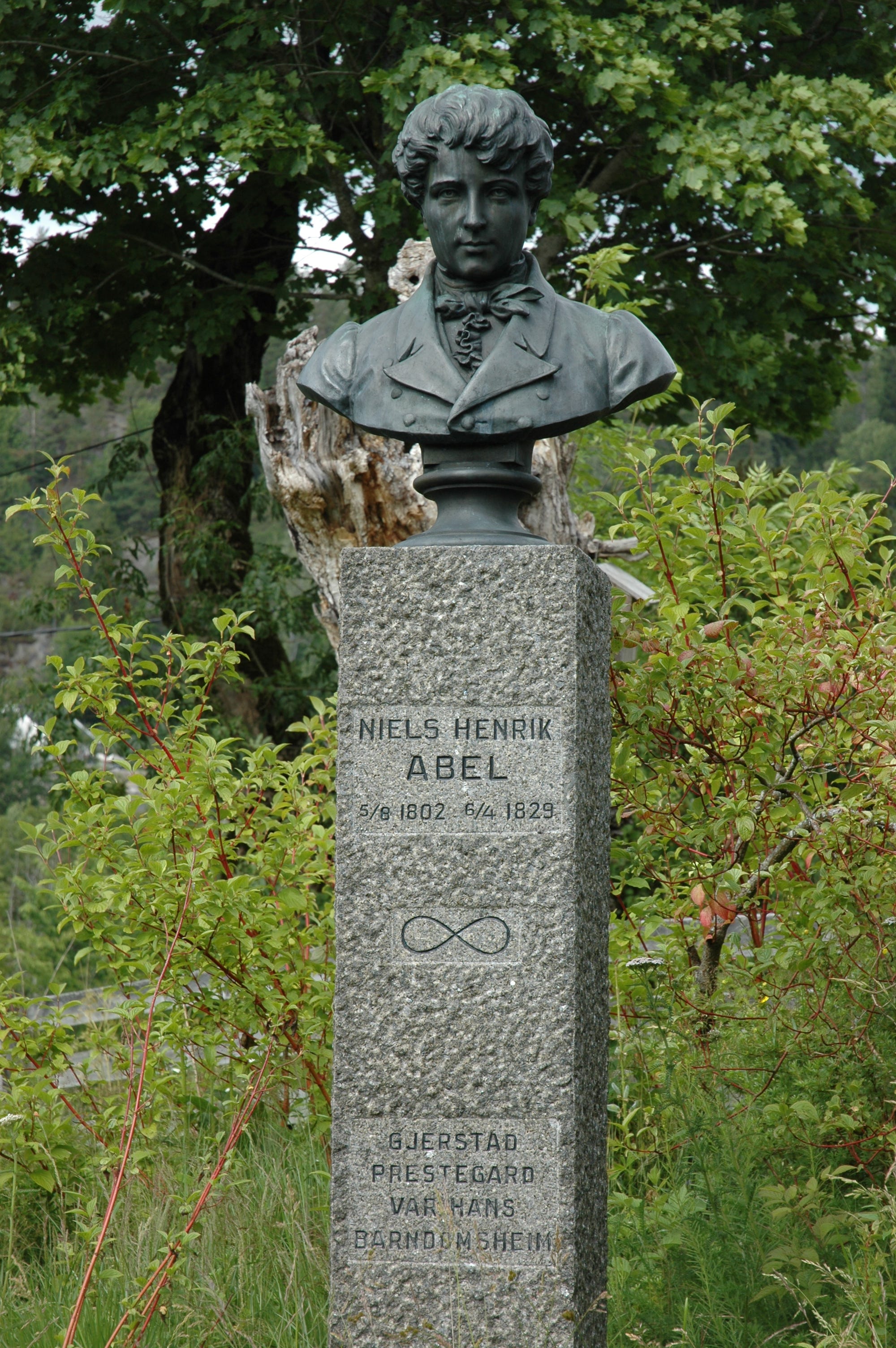
Left: The Abel Bust by Brynjulf Bergslien in Gjerstad, Norway. Right: Gjerstad Kommune in the Agder region of Southern Norway

Monuments in his memory have been erected in the Royal Palace Park in Oslo, outside of his house on the campus of the University of Oslo, in his hometown of Gjerstad, on his birth island of Finnøy and more. Abel’s likeness has also been featured on Norwegian banknotes, commemorative coins, stamps, and his name given to a crater on the moon, an astroid and an aircraft.

The Abel Prize

In memory of his short but eventful life, the Norwegian government in 2001 announced that it would award a yearly mathematics price in the memory of Niels Henrik Abel, beginning on the two-hundredth anniversary of his death in 2002. Winners of the prize as of 2020 include:

Winners of the Abel Prize as of 20202002: Atle Selberg (memorial)
2003: Jean-Pierre Serre
2004: Michael Atiyah and Isadore Singer
2005: Peter Lax
2006: Lennard Carleson
2007: S.R.Srinivasa Varadhan
2008: John G. Thompson and Jacques Tits
2009: Mikhail Gromov
2010: John Tate
2011: John Milnor
2012: Endre Szemerédi
2013: Pierre Deligne
2014: Yakov Sinai
2015: John F. Nash Jr. and Louis Nirenberg
2016: Andrew Wiles
2017: Yves Meyer
2018: Robert Langlands
2019: Karen Uhlenbeck
2020: Hillel Furstenberg and Grigory Margulis

Those interested in reading more about the life and works of Niels Henrik Abel are encouraged to acquire the following books and articles:

* This is an Amazon Affiliate link

Read more