The Most Beautiful Equation in the World

Before we begin our quest towards understanding the beautiful fact called Euler’s Identity, let’s warm up with an amazing piece of history.

Numbers in Love

About 500 b.c. the Greeks regarded some numbers as more important than others. In particular, they knew of two numbers with a remarkable property. The two numbers are 220 and 284.

Before explaining why these numbers are so interesting, we need to know what a proper divisor is. Well, it is very simple. A proper divisor of say, n, is a natural number smaller than n, that divides it. So for example, the proper divisors of 6 are 1, 2, and 3. Now, the reason that the two numbers above are interesting is that the sum of the proper divisors of 220 is 284 and the sum of the proper divisors of 284 is 220. This relationship is called amicability and the numbers are called amicable numbers (amicable meaning friends or lovers). In fact, it used to be a tradition for two lovers to pick up a fruit, write one of those two numbers on one half of the fruit, the other number on the other half of the fruit, divide the fruit into the corresponding two halves, and then consuming a piece each. This would “unite them and their love forever”.

The Greeks regarded this as a very important relationship but they couldn’t find any more of such numbers no matter how hard they tried. It remained that way for about a thousand years until Thābit ibn Qurra found two more pairs in the 9th century. Back in those days, the center of mathematics had moved from Europe and Egypt to the Arabic world where it would remain for almost half a millennium.

Thabit’s discovery along with further progress in e.g. Iran was however not carried to Europe where only one pair (from the Greeks) was known. That was until Fermat found a pair in 1636. The amicable numbers he found was 17,296 and 18,416.

In this period, there was a mathematical civil war going on between two mathematical giants. Namely, Pierre De Fermat and René Descartes. They hated each other and now Fermat had found a pair of amicable numbers, therefore Descartes had to find another. In 1638 he finds the pair 9,363,584 and 9,437,056. This, I remind you, is without a calculator! It must have been some long rainy days.

It turns out that these two pairs that Fermat and Descartes had found were the same pairs that Thābit had found.

Thus, the status of amicable numbers remained at only three known pairs after 2000 years of bright minds and rainy days…

Then Euler decides to give it a try.

Euler finds 58 more pairs of amicable numbers!

That is wildly insane. Of course, what happened was not brute-force trial and error. Instead, Euler found a method relying on properties of the sum-of-divisor function as well as some genius insights.

Are there infinitely many, you ask? No one knows… This is again, one of the mysteries of mathematics.

The Most Beautiful Equation

Euler is famous for many things amongst mathematicians, but one beauty shines a little brighter than the others. It has been called the most beautiful equation in all of mathematics though technically, it is what’s known as an identity.

I will explain this result in a couple of different ways so that the reader will get an intuition as well as a mathematical understanding of it (sketch of proof).

First, let’s state it.

Euler’s Identity (1748):

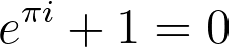
So why is this relation so beautiful?

Well, first of all, as William Dunham puts it:

If you wanna do addition you need 0, if you wanna do multiplication you need 1, if you wanna do calculus you need e, if you wanna do geometry you need π and if you wanna do complex analysis you need i. This is the dream team of numbers and they are all in this one equation.

Let’s back down a bit and define the numbers before explaining the identity.

0 and 1

0 of course is a number, but it is a very special number. It is the limit between the negative and the positive numbers, it is the only number you can’t divide by, and most importantly, it is the additive identity, which means x + 0 = x for all numbers x.

This may look trivial, but in fact, it is a big deal since it’s a vital part of what is known as a group in mathematics. Group theory is the mathematics of symmetry, but that’s for another article. Likewise, the number 1 is, of course, the multiplicative identity.

π

We have already met π, and π is everywhere in math.

From number theory to probability and trigonometry, but why is this?

Well, circles are related to both symmetry and periodicity, and these phenomena are occurring in a lot of different events in nature and places in mathematics. From the permeation of heat to random walks and the vibration of electromagnetic waves (or guitar strings for that matter), to densities of statistical distributions, and much much more.

The definition of π is of course a circle’s circumference divided by its diameter (any circle, mind you) and even though it is defined as a ratio, it cannot be written as a fraction of whole numbers. It is what we call irrational (in fact transcendental). A superstar of math for sure!

e

Now, what about the number e? This number is a little harder to define, but we will give it a try.

First of all, e is a number about 2.7182818, first discovered by Euler himself in 1748. I can’t write down all the decimals because it is also irrational (and transcendental). Euler also discovered how to calculate it:

This is actually how Euler would have written it in 1748. Today we tend to compress it with fancy notation but I won’t bore the reader with that.

If you have ever done calculus or maybe just differentiated some functions a long time ago, then you might remember that there is an identity for the differential operator, namely the function

i.e. it has the property:

which is extremely important since, for one, it makes us capable of solving differential equations. Since almost all of the physical laws and systems can be described by differential equations, these are pretty important in physics, biology, mathematics, and science in general.

You can therefore describe the number e as the base of the exponential function with the property that the rate of change at a given moment is equal to its value at that moment.

i

Okay. So what is the number i? For many years, people wouldn’t accept i as anumber, but then again, they wouldn’t accept negative numbers when they first appeared, so I guess it is a matter of maturity.

In Euler’s time, they didn’t know very much about this number. Now, the study of i and the functions that use it is known as complex analysis, and of course, Euler lead the way in this exotic new area from the beginning.

As with many other things in math, i can be defined in many different ways. Some more formal than others. We will stick to the simplest (and most non-technical) definition. i is the number with the following property:

Of course, there is no real number satisfying this, because if you multiply two negative numbers, you get a positive number. We sometimes call it the imaginary unit.

A complex number is a number of the form a+bi where a and b are real numbers (numbers as you normally think of them, either negative, zero, or positive). Complex analysis is the study of complex-valued functions of complex variables and is (in my opinion) one of the most beautiful subjects of mathematics.

But… What can you do with them?

Glad you asked. Surprisingly, many real-world calculations depend on complex numbers, from radar technology to the solution of differential equations and quantum mechanics to name a few.

Great. Now we know the players on the field. The next question is of course whyEuler’s Identity is true.

To answer that question, we need to think a little open-minded and differently about mathematical operations and numbers.

The duality between operations by numbers and geometric transformations

First, I want to stretch your imagination a little. So imagine the number line i.e. the real numbers from negative infinity to infinity and zero in the middle.

Of course, you need enough RAM in your mind to contain an infinite chunk of topology, but it gets better. We will now think about what will happen if we decide to add all the numbers on the number line by 2. In our minds, we will view the whole thing from above as it happens at once.

In this scenario, -2 goes to 0, -1 goes to 1, 0 goes to 2, and so on. In other words, the whole real number line will shift by 2. This transformation is called translation.

If you add by 0, then no shift will occur.

What if we decide to subtract, that is, adding with a negative number? Well, the basic transformation is the same (translation) but it is the inverse transformation (corresponding to a shift in the other direction). Therefore adding and subtracting by the same number corresponds to shifting left and right by the same amount in each direction getting you back to where you started. And that of course is equivalent to adding by 0 i.e.

x - x = x + (-x) = 0.

Okay, so adding and subtracting is really about the translation transformation. How about multiplication?

Well, by thinking about it in the same way as above, you can see in your mind’s eye, that multiplication by a positive number is really about dilation (stretching) the number line. How about division? Division is actually multiplication in disguise (for example, dividing by 2 is the same as multiplying by 1/2), and like before is the inverse transformation. It is about zooming in or zooming out.

Of course, the identity of this transformation corresponds to multiplying by 1(scaling by 1 does nothing).

But how about multiplying by a negative number? See, that is a great question. What transformation does that correspond to?

First, we need to remember that multiplying by -x is actually the same as first multiplying by x and then by -1. So When we multiply by that, we first do a dilation, by x and then the transformation corresponding to multiplying by -1.

It thus suffices to find out what multiplying by -1 does.

It turns out that multiplying a real number by -1 corresponds to a reflection through 0. You can see this by taking a number x on the number line and multiplying by -1. Then you land symmetrically on the other side of 0 at -x. This also holds when x is negative.

Note that now it also makes sense that negative times negative is positive. If you reflect two times you get back to where you started. In mathematical language (-1)(-1)=1.

When I first discovered the dual relationship between transformations and operations by different numbers, I was struck by a feeling of beauty and completeness. Also because no one had ever explained to me why a negative number multiplied by a negative number is a positive number. But here it is! It is because the transformation of two reflections about the same line is equal to the identity transformation i.e. the one that does nothing. The identity transformation here translated into numbers and operations corresponds to the action of multiplying by 1.

It turns out that this can also be explained by the field of Ring Theory using something called homomorphisms but this is a little more advanced and I learned this a lot later. I still think that the geometry of numbers is a more beautiful approach.

Now we have explained how the real numbers with the classical operations fit together with their corresponding transformations and what they really are but we are lacking an important transformation — rotation.

Let’s think about this for a while. Rotating numbers that live on the real line counter-clockwise by some angle sounds exotic and dangerous. After all, if we are not careful, we could end up in an alien world far from home, outside our number line, trapped in another dimension.

It sounds like we have to invent some new weird numbers that live in a two-dimensional number plane, not to solve hard equations, but for the completeness of our transformations.

This, by the way, happens a lot in mathematics. You look at something from a different angle and discover interesting new things.

Okay. So what’s the property of these alien numbers then? Hmm. Let’s take the number that when we multiply by it, corresponds to rotating counter-clockwise by 90 degrees.

First of all, we can get the position of this interesting number by multiplying it by 1, since that should equal itself, but it should also be the same as the number we end up with if we rotate 1 by 90 degrees.

Therefore this new number is located at the point (0, 1) on our number plane where in this new number system, our old friend 1 is now the point (1,0).

Obviously, when we multiply by the square of this number, we rotate by 180 degrees. So the square of this number sends 1 to -1.

Thus the square of this mystical number is just -1.

Dear friends, what we have deduced now is that this number is exactly the number i — the imaginary unit from above. So i is the number located at (0,1) in our number plane.

So the set of complex numbers falls right out of the box as a very needed and natural set of numbers and they are responsible for the rotation transformation. It turns out that the complex number a +bi is nothing more than the point (a, b)in what is now known as the complex plane (what we called the number plane before).

This means that all our numbers actually live in a two-dimensional world where each point corresponds to a complex number including the real numbers that are just embedded in the complex plane as a (proper) subset. Therefore all real numbers are also complex numbers but not all complex numbers are real (obviously).

This geometric view was not available to Euler since it was first developed later by Caspar Wessel, Carl Friedrich Gauss, and others. So Euler just saw i as a number with the negative square property that defines it.

Now that we understand numbers from this perspective and with this duality in mind, we only need one more ingredient before we can understand Euler’s identity intuitively.

Though before revealing this ingredient, we need to know what radians are. Think about it, why are there 360 degrees in a circle?

It turns out that it is a left-over from the Babylonians and their hexadecimal number system. No disrespect to the number 60, but it is quite arbitrary (not totally arbitrary but that’s a long story) and mathematicians don’t like that. Things should be natural.

So we calculate “degrees” in another way. It is all about the normalized circle with radius 1, the so-called unit circle. This circle defines the trigonometric functions i.e. cosine, sine, tangent, secant, etc., so it is quite natural to use this to define degrees.

The idea is that instead of choosing an arbitrary number as “the whole way around”, we simply choose the circumference of the unit circle as that. So 360 degrees corresponds to 2π radians, 180 degrees corresponds to π radians, and so on and so forth.

Now we are ready for the final ingredient.

The following is a fact that we will give a sketch-of-proof of in a bit, but for now, we will just state it here:

When we multiply any complex number z (including the reals remember?) by the number

then the result is z rotated by θ radians.

Now, we are ready to take a look at Euler’s identity again with our new understanding of the numbers and their operations with each other. It has been a while so let’s revisit it, but this time written a little differently.

So what is this saying?

Well, it is very simple really. We know that the left-hand side just says: “rotate by π radians” which is 180 degrees remember? and the right-hand side says: “reflect through the number 0”.

So what Euler’s identity is really saying is the following:

A rotation of 180 degrees is the same as a reflection through 0.

Simple, beautiful, elegant!

Okay, so now we understand it from a geometric view and that is of course nice, because now we have some images associated with the equation, but this is hardly a proof. It is almost a proof, but we never showed how the number e is related to a complex number’s angle associated with it (called its argument). Also, I want to show you how Euler proved his identity.

Euler shows the relationship between angles and the exponential function in a more general result (also an identity), namely

Euler’s Formula (1748)

Before proving this, let’s sit back and appreciate this result a little.

First of all, it means that the exponential function is periodic! It may not look like it when you plot its graph but that’s because its period is imaginary. The period is of course 2πi because cosine and sine both have period 2π (note that we are talking about the trigonometric functions defined in terms of radians and not degrees as you may have studied in high school).

Let’s quickly go through Euler’s proof of this.

You might recall from the last essay that we can write some functions as a power series called Taylor series. Here it is:

First, he writes out the exponential in its Maclaurin series.

Then he pulls i out of parenthesis. Note that the series inside the parentheses on the right alternates because if you raise the imaginary unit to a number on the form 4n you get 1, 4n+1 you get i, 4n+2 you get -1, 4n+3 you get -i.

After this, he recognizes (of course he does) the two series inside the parentheses as the Maclaurin series of cosine and sine, respectively. You might recognize the sine function in this representation from the proof of the Basel problem in the first part of this series called Infinity in Numbers — Leonard Euler.

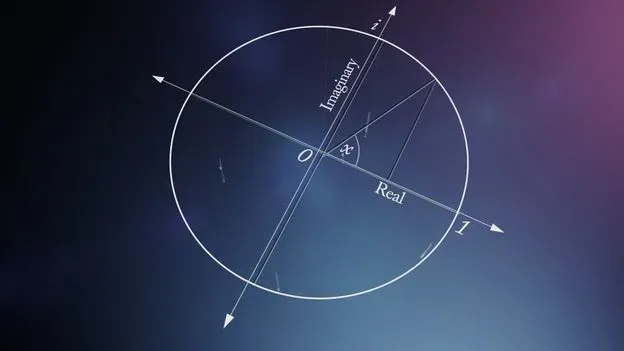
To explain the relationship between the exponential function and angles, imagine a complex number as a point on the complex plane with coordinates (a, b). This number can be written a+bi and it has a distance to the origin. Let’s call this distance its length (or modulus) r. Now, how about the angle to the real line?

Well, if we draw a line from our point (a, b) down to the real axis (the real number line) parallel to the imaginary axis and we also draw a line from our point to the origin, we form a right triangle. The angle at the origin is exactly the argument of the complex number a+bi and in our language of transformations, it is the angle that the number rotates other numbers by when we multiply by it.

To find the argument (or angle) of the complex number, we remember from trigonometry that when the length of the hypotenuse is r, then sine of the angle multiplied by r is the length of the opposite side and cosine of the angle multiplied by r is the length of the adjacent side.

In other words, in our complex number a+ib, we have a = rcos(θ) and b = rsin(θ). And so

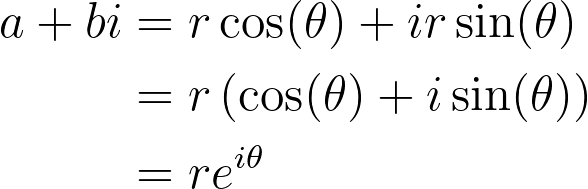
where we have used Euler’s Identity in the last equality. In other words: any complex number a+bi can be written in this polar notation in terms of its argument and modulus by the exponential function.

But how does Euler’s more general identity prove his “dream team” equation?

Well, if x = π, the sine term vanishes (becomes 0), and the cosine term becomes -1 because pi radians is 180 degrees.

This finally proves his beautiful equation with some small detours.

Some say that Euler is the greatest mathematician ever to have lived and some say Gauss but in the end, it doesn’t really matter. The thing that matters is that we indeed are standing on the shoulders of giants.

The way of telling the anecdote about amicable numbers, in the beginning, is hugely inspired by the awesome and colorful teachings of William Dunham.

In the next part of this series, we shall discuss some beautiful insights by Euler which lead to a brand new field of mathematics — Topology.

Read Euler, read Euler. He is the master of us all

~ Pierre-Simon Laplace