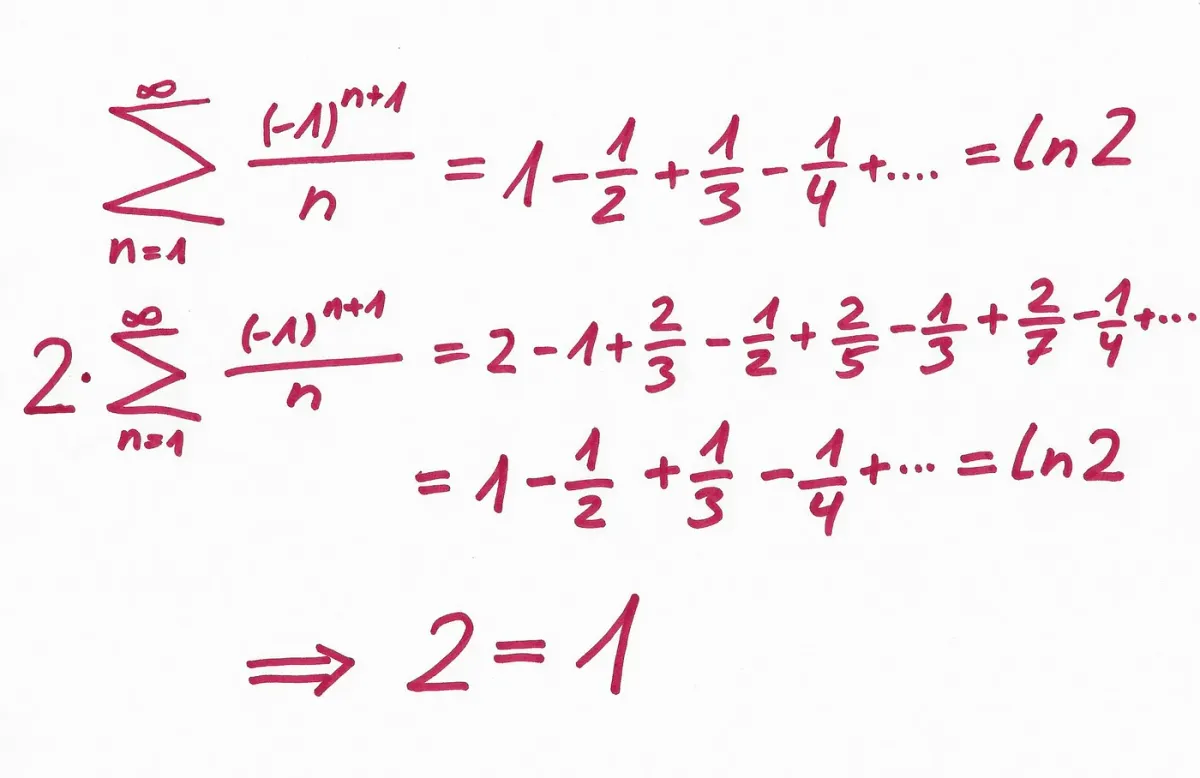
Mathematical rules are commonly applied without any thoughts that it could not hold in a particular situation. But sometimes, mathematics can be surprising for non-mathematicians.

We are all used to the so-called commutative law for addition.

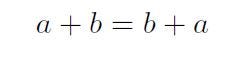
And we all know that it does not only apply for two numbers, but we can rearrange the summands of longer sums like

Well, this is generally true, as long as the sum is finite. That is a critical but often unverbalized assumption.

So, what happens, if we weaken this assumption and take an infinite sum?

Let’s turn to the alternating harmonic series. The alternating harmonic series is of the following form, and it converges to the natural logarithm of 2.

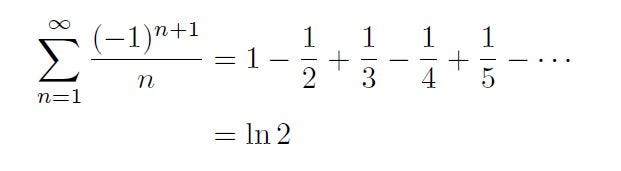
Or graphically,

(please be aware that the integral has to be taken over the interval [1,2] because of the definition of the logarithm and its non-existence at 0)

Now, we multiply both sides by a factor of two and rearrange the whole series by summing up all terms with the same denominators.

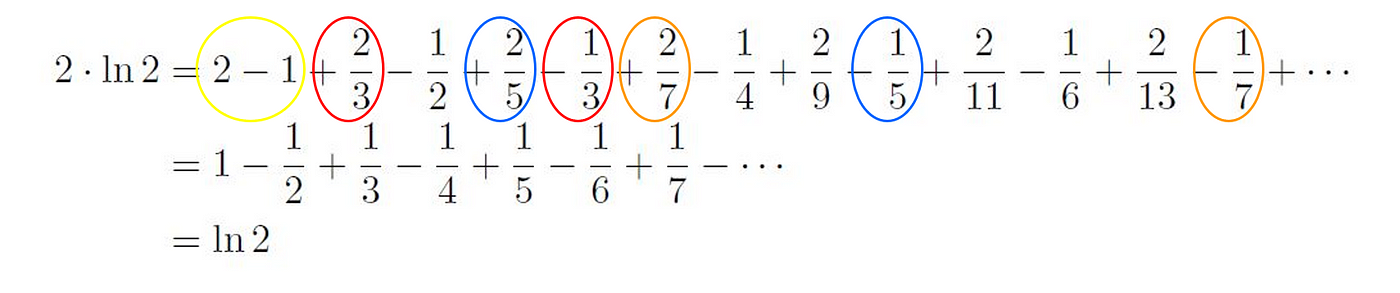
By dividing both sides by ln 2, we get

2 = 1

It seems that we have just proved one of the famous jokes made in mathematics, or that our mathematical system is indeed wrong.

Fortunately, none of these two suspicions are correct.

Peter Gustav Lejeune Dirichlet discovered this mind-boggling result in 1827 while working on the Fourier series’s convergence properties. He was the first person who realized that rearranging the summands of particular series are changing the sum. While giving him the crucial input to solve the Fourier series’s convergence problem in 1829, he never was able to find an answer throughout his life why this is possible.

I can understand when many of you do not believe that either and search for the error. So, here is another example. The proof is a bit more complex — one must take an 8, 4, 8, 4, … scheme of the number of summands and put them together in a block — and I omit it.

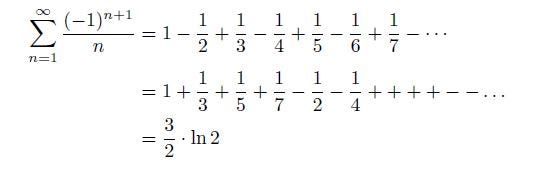
And, some rearrangements of the alternating harmonic series must not even converge.

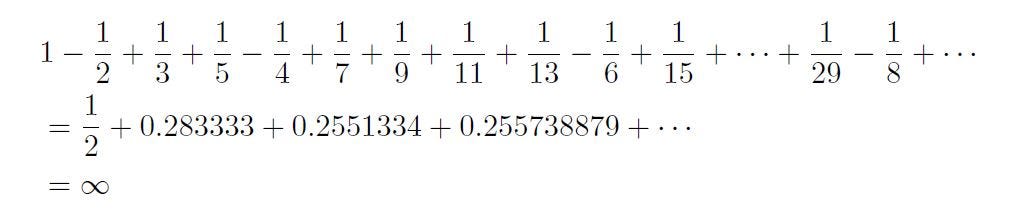
The idea is to build blocks where we sum first 2ᵏ positive terms and then subtract only one negative summand such that each partial sum is bigger than 1/4. And the sum of infinite terms of 1/4 is, of course, infinite.

Why does this happen?

Georg Friedrich Bernhard Riemann started in 1852 to work on Dirichlet’s convergence properties of the Fourier series, and the two had exchanges about the topic. In their discussions, Dirichlet mentioned his discovery that rearranging the terms of specific series leads to different sums.

That finally lead to Riemann’s Rearranging Theorem in 1853, but has only be published after Riemann’s death in 1866 in “Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe (1867)” — or translated to English “On the representation of a function by a trigonometric series.”

To understand what Riemann’s theorem states and why this strange behavior of series can happen but explained, we first need two definitions.

And this is the key to the property of the alternating harmonic series. The series is not absolute convergent.

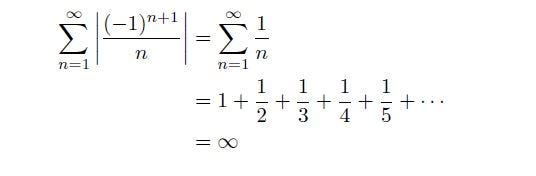
But conditionally convergent because the series converges.

I will skip here all the testing criteria when a series is convergent or divergent. There are many of them, and it requires more in-depth mathematical knowledge. Should you be interested in knowing more about these criteria, I recommend the lecture notes of Dr. P. Shunmugaraj and, for more advanced tests, the notes of Sarah Fix and Professor Russell A. Gordon.

That leads us finally to Riemann’s rearrangement theorem.

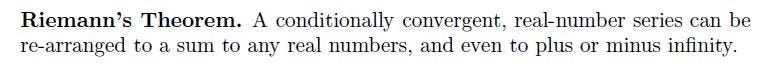
You may ask why such properties can be of broader interest. While seeing that absolute convergence is useful in practice, e.g., calculating irrational numbers to a certain accuracy, why we also need conditionally convergence?

Riemann’s theorem gives a simple algorithm for convergence to any real number within a given error bandwidth. Based on the theorem, one can sum up positive summands, and then by subtraction to correct the sum to the direction of the desired value. Repeating this procedure gives you the value within an error tolerance. How do you want to achieve that otherwise?

Look at the following two examples by rearranging the alternating harmonic series. By selecting a summand, we always start from left to right, meaning we pick the first summand from the left that fulfills the chosen criteria, and then we form blocks of summands as shown above.

1. In the first one, we always take one positive term, followed by 36 negative summands. The sum will converge exactly to -ln 3.
2. In the second case, we take 375 times a positive summand and 203 negative summands. The sum is oscillating around 1, and it converges almost to 1 within a specific bandwidth, but not precisely.

That raises questions:

• Why does it converge in the first example exactly, but in the second only almost?
• How do we decide to choose the blocks?

Let label the number of positive summands combined in a block by p, and the number of negative terms combined in a block labeled by n. Then, there is a result (see, e.g., Knopp, 1971) that shows

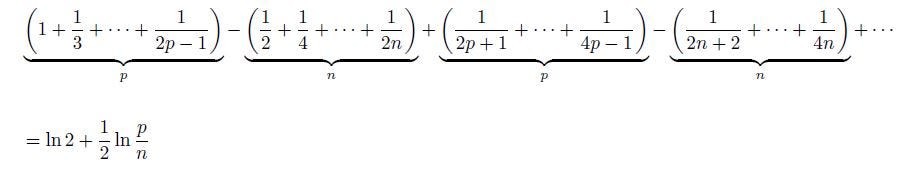
That means, for every number that can be represented by this formula, like -ln 3, by letting p=1, and n=36, we have exact convergence, whereas, for all other numbers, we must approximate it, e.g., with p=375, and n=203 for an approximation of 1. And that defines the simple algorithm of Riemann to approximate each real number.

Summary

Having a deeper understanding of the alternating harmonic series’s amazing properties is not only beneficial for education in mathematical thinking. It gives a great benefit to today’s computational thinking. And it shows what a genius Bernhard Riemann was.

References

• M. Barner, und F. Flohr, Analysis I, 4. Auflage 1991, Walter de Gruyter & Co., D-1000 Berlin 30
• C. Blatter, Analysis 1, 4. Auflage 1991, Springer-Verlag Berlin, Heidelberg, New York
• I. Grattan-Guinness, The Development of the Foundations of Mathematical Analysis from Euler to Riemann. 1970, Cambridge, MIT Press
• K. Knopp, Theory and Application of Infinite Series, 1971, Hafner Publishing Co., New York
• A. Pringsheim, Ueber die Werthveränderungen bedingt convergenter Reihen und Producte, S. 455, Mathematische Annalen 22 (1883) 455–503
• B. Riemann, Über die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe, Gesammelte Mathematische Werke (Leipzig 1876): 227–71