Chess-players are rated according to how well they perform when facing other players. For example, reigning World Chess Champion and fellow Norwegian Magnus Carlsen is as of September 2019 rated by the International Chess Federation FIDE (Fédération Internationale des Échecs) at 2876 points, the highest in the world yet six points shy of his own peak rating of 2882 in 2014 when he was 24 years old.

The rating system used by FIDE and nearly all other chess federations is called the Elo rating system. It was introduced in 1960 by the United States Chess Federation at the suggestion of a Hungarian-American chess master whose name it has carried since, Arpad Elo. Elo’s system tracks the relative performance of players in zero-sum games such as chess. Based on the assumptions of

1. Performance behaving as a random variable
2. Performance conforming to a bell-curve shaped probability distribution
3. Mean performance of players changing slowly

the system allows one to sort a group of players by relative performance, and so make educated, probabilistic guesses about expected outcomes of games and variation in player performance over time.

History

Prior to the invention of the Elo ratings system, the United States Chess Federation (USCF) used a numerical rating system devised by Kenneth Harknesswhich tracked individual players’ performance in terms of wins, losses and draws. The Harkness rating system was in use from 1950 to 1960. It calculated the average rating of a player’s competitors in a tournament. If a player scored 50%, they received the average competition rating as their performance rating. If they scored more (less) than 50%, their new rating was the competition average plus (minus) 10 points for each percentage point above (below) 50%.

Arpad Elo

Enter Emre Arpad Elo (1903–1992). Elo had been a master-level chess player and active participant in the United States Chess Federation (USCF) since its founding in 1939, when he on the organization’s behalf in the 1950s devised a new system for rating players based on known ideas from statistics including expected value, random variables and probabilistic distributions. Elo had been educated in physics at the University of Chicago and became a Professor of Physics at Marquette University in Milwaukee where he also won the Wisconsin State Chess Championship eight times.

Given his background, the USCF in 1959 asked Elo to improve the Harkness rating system used in the US chess community. Elo proposed his new system the same year, adjusting his formula to the existing rating system so that players’ ratings wouldn’t deviate much from the numbers they were used to. According to his new system an average player was rated 1500, a strong Chess club player 2000 and a grandmaster 2500 (Chessbase, 2003).

Elo made use of papers of Good (1955), David (1959), Trawinski & David (1963), and Buhlman & Huber (1963) in his proposal, which was adopted by the USCF in 1960 and by FIDE in 1970. Elo later described his work in the book The Rating of Chessplayers, Past and Present (Elo, 1978), and among other things (now famously) stated that:

“The process of rating players can be compared to the measurement of the position of a cork bobbing up and down on the surface of agitated water with a yard stick tied to a rope which is swaying in the wind”. — Arpad Elo

Performance

The key characteristic of the Elo rating system is that performance is not measured absolutely, but rather inferred from wins, losses and draws against other players of varying ratings. In other words, players’ ratings depend both on their performance and on the ratings of their opponents.

Specifically, the difference in rating between two players determines an estimate of the expected score between them. Elo’s key assumption is that the performance of each player in each game is a random variable which over time conforms to a Bell curve-shaped probability distribution. In other words, in Elo ratings systems, a player’s true skill is represented by the the mean of that player’s random performance variable. For chess, Elo suggested scaling ratings so that a difference of 200 ratings points would mean that the stronger player has an expected score of approximately 0.75.

The expected performance of a player in the Elo rating system is a function of their probability of winning + half their probability of drawing. In other words, an expected score of 0.75 could represent a 75% chance of winning, 25% chance of losing and 0% chance of drawing.

More specifically, if chess players A and B have ratings Rᴬ and Rᴮ, respectively, the expected score of players A and B are given by:

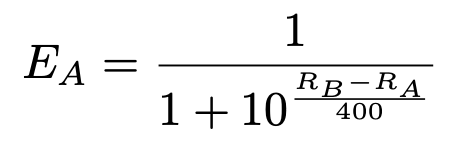
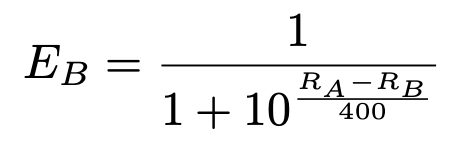
When a player’s scores exceed (fall short of) their expected scores, the Elo rating system assumes that the player’s rating had been too low (high) at its outset, and so needs to be adjusted upwards (downwards).

Distribution

In Elo’s original proposal to the USCF, the system assumed that players’ expected scores conform to a normal distribution. Later, both the USCF and FIDE altered their systems when it was found their empirics suggested that performance in chess more resembles a logistic distribution (heavier tails/higher probability of extreme outcomes).

K-factor

The maximum possible adjustment per game in the Elo rating system is called the K-factor. In the original proposal it was set to be K = 10 for players rated above 2400, meaning the rating system should (in a sense) discount the importance of individual events and instead factor higher the trend of the time series, i.e. the evolution of the mean performance of a player over time. Empirical observation has indicated that as opposed to Elo’s proposed K = 10 value, K = 24 may be more accurate value (Sonas, 2002). Currently, the USCF uses a three-level K-factor for players below 2100, between 2100–2400 and above 2400 of 32, 24 and 16, respectively. FIDE uses similar factors (40, 20 and 10) albeit with somewhat different rules.

Vulnerabilities

As with all models which assume a random variable, the Elo rating system is vulnerable to selective pairings and unrepresentative populations, which render the model inaccurate. For instance, given the shape of the logistic distribution curve, a higher rated player which has the option to choose which games to accept might reject games against opponents in which the probability of loss is high and instead play lower rated players whose expected performance is much lower. Similarly, in isolation, a selection of players which is unrepresentative of the global population of chess players will generate ratings which are unrepresentative of their expected performance as compared with players from the global population.

FaceMash

The predecessor to the social network Facebook was a website created by Mark Zuckerberg in 2003 which ranked female Harvard students by comparing two student pictures side-by-side and letting visitors vote on who was more attractive. The website called FaceMash used an Elo ratings system to determine which students’ pictures should be presented side-by-side.

In this application, ‘expected performance’ (Ea) may be interpreted as “expectation that student A is more attractive than student B” and ‘rating’ (Ra) as “rate at which student A has been voted more attractive than student B”.