The Mathematical Center of the Universe

The inception of quantum mechanics can essentially be traced back to a single “Golden Age” in the mid-1920s at one university: the Georg-August University of Göttingen, in the city of Göttingen in Germany. Home to many notable scientists, the university is associated with no less than 45 Nobel Prize winners. Included in this group are many of the figures responsible for the creation of quantum mechanics, such as Max Born, Werner Heisenberg, James Franck, Wolfgang Pauli, Eugene Winer, Paul Dirac, Enrico Fermi and J. Robert Oppenheimer.

At the outset of the 19th century however, the University of Göttingen was first and foremost considered a prime research institution for mathematics, a status it would hold until the “Great Purge” of 1933 forced many of its most talented academics to flee Germany for institutions in England and the United States.

This essay is about the mathematical center of the universe prior to World War II, the University of Göttingen.

History

Prior to the 19th century, the University of Göttingen was primarily known for its Faculty of Law, so much so that at its centenary in 1837 it was known as “The University of Law”, in particular public law. Among its most notable alumni at the time were later founder of the University of Berlin, Wilhelm von Humboldt and Otto Bismarck, the creator and first Chancellor of the second German Empire.

Enter Carl Friedrich Gauss (1807–1855)

Most notable among Göttingen’s early faculty at the turn of the 19th century — by a landslide — was Carl Friedrich Gauss (1777–1855). Gauss first arrived as a student in 1792. He remained there until 1798. His doctorate in 1799 was completed in absentia, but he returned to Göttingen in 1807 at the age of 30 to assume the position of Director of the Göttingen University Observatory, a post he held for the rest of his life. Gauss’ countless discoveries while at Göttingen include his work in algebra including his Ph.D. dissertation which proved the fundamental theorem of algebra, a proof of Fermat’s polygonal number theorem for n=3, Fermat’s last theorem for n=5, Descartes’ rule of signs and the Kepler conjecture for regular arrangement.

While at Göttingen, Gauss supervised the doctoral dissertations of several other brilliant mathematicians, including Bernhard Riemann (1826–1866) who arrived in Göttingen in 1846 to study theology before being enchanted by Gauss who convinced him to instead pursue mathematics. Riemann, who only lived to be 39 years old, famously invented the Riemannian geometry later used by Albert Einstein to prove the general theory of relativity. In addition, Riemann established the geometric foundation for complex analysis through the use of Riemann surfaces, the Riemann integral, and in a single, four page paper on number theory demonstrated the properties and importance of the Riemann zeta function, and in particular its intimate relationship with the distribution of prime numbers.

Gauss’ last student and Riemann’s contemporary Richard Dedekind (1831–1916), studied at Göttingen from 1850 until he was awarded his doctorate in 1852. Under Gauss, Dedekind studied Euler integrals. His most well-known result is likely Dedekind’s theorem which states that if there existed a one-to-one correspondence between two sets, then the two sets are “similar”. From this work, he developed a close relationship with Georg Cantor and indeed corresponded with Cantor as he was developing his theory of infinite sets and ordinal numbers. Dedekind also later edited the collected works of Gauss, Riemann and Dirichlet for publication. His study of the latter’s work led him to later investigate algebraic number fields and ideals. He was also among the first to lecture on Galois theory at Göttingen and to realize and promote the importance of groups in algebra and arithmetic.

Following the death of Gauss in 1855, the Friedrich-Wilhelms-Universtät briefly inherited the crown as the main institution for mathematical research in Germany (and so the world). Prominent on Berlin’s faculty at the time was Lejeune Dirichlet (1805–1859), one of Gauss’ students, who began lecturing there in 1831. He eventually also returned to Göttingen, having completed all of the formal requirements for becoming a full professor in 1851. Dirichlet, who worked for a time with Dedekind, is now most known for his deep contributions to number theory, including the founding of the field of analytic number theory which Riemann’s renowned 1859 paperUeber die Anzahl der Primzahlen unter einer gegebenen Grösse, “On prime numbers less than a given magnitude” regarded. In addition however, Dirichlet also published in analysis, including investigations into Fourier series and partial differential equations.

Dirichlet was in 1855 appointed to become Gauss’ successor at Göttingen, a position he held until his own passing four years later (of a heart attack) in 1859. The university preserved both professors’ brains in their department of physiology, where they still remain to this day.

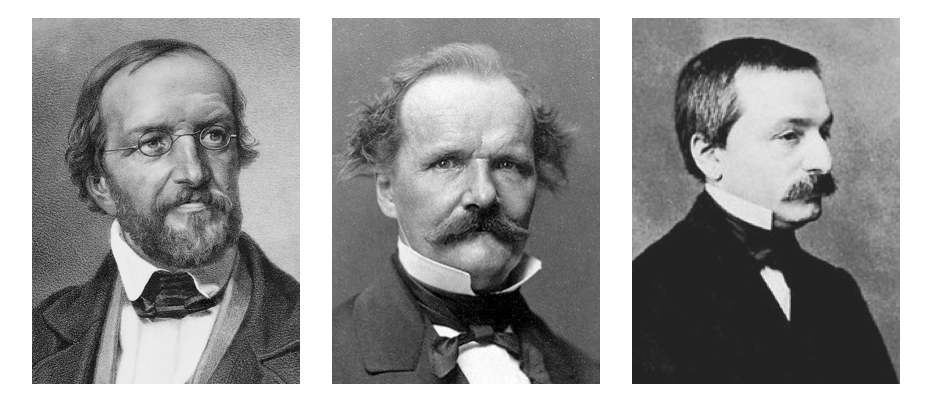
Replacing Dirichlet as professor of mathematics in Berlin when he went to Göttingen was Ernst Eduard Kummer (1810–1893), a former high school teacher whose doctorate had been completed at the University of Halle in 1831, also under the partial supervision of Gauss. While a high school teacher, Kummer had himself inspired a young Leopold Kronecker (1823–1891) to pursue a career mathematics, which Kronecker did in Berlin under Dirichlet starting in 1841 until obtaining his doctorate in 1845. Although conducting important fundamental work in number theory, algebra and logic, Kronecker is by now perhaps best known for his ardent rejection of Cantor’s work.

Around the same time as Kronecker obtained his doctorate, Gauss’ star pupil Riemann also transferred to Berlin, where he stayed for two years before returning to Göttingen in 1849. The German university system at the time allowed students to easily move from one university to another. Dedekind, Riemann’s closest contemporary transferred to Berlin as well. They both received their habilitation in 1854. Afterwards they both returned to Göttingen as Privatdozents. Dedekind stayed until 1858 when he left for ETH Zurich, while Riemann as mentioned tragically died of tuberculosis in 1866.

In the latter part of the 19th century, Göttingen had hence seen the death of three of its most prominent stars: Gauss in ‘55, Dirichlet in ’59 and Riemann in ‘66. From then until the end of the century the faculty’s most notable member was arguably Felix Klein (1849–1925), most known for his work on group theory (promoted by Dedekind), complex analysis and non-Euclidean geometry (both pioneered by Riemann) and the invention of the one-sided closed surface the “Klein bottle”. Meanwhile, in Berlin, the father of modern analysis Karl Weierstrass (1815–1897) arrived as a full professor in 1864. Despite never obtaining an academic degree, Weierstrass formalized the definition of the continuity of a function, proved the intermediate value theorem and the Bolzano-Weierstrass theorem.

Physicist Max Planck (1858–1947) first arrived in Berlin in 1889, having been appointed the successor to Gustav Kirchhoff (1824–1887), the physicist who both coined the term black-body radiation (later described by Albert Einstein in his 1905 Nobel Prize-winning paper) and contributed to the fundamental understanding of electrical circuits and spectroscopy. Planck, who is credited with the discovery of energy quanta and so as the originator of quantum theory, although working for most of his life in Berlin, was both born in Göttingen and buried there upon his death in 1947. His discovery of energy quantum won him the Nobel Prize in Physics in 1918. Around the same time as Planck’s arrival in Berlin, Edmund Landau (1877–1938) began his university studies at the same university, completing his doctorate in 1899, the same year he began lecturing as a privatdozent. By 1909, still a privantdozent, Landau had published over 70 papers when he was appointed to an ordinary professorship at Göttingen, succeeding Hermann Minkowski (1864–1909). Minkowski is now perhaps most well-known of this development of the geometry of numbers and invention of the Minkowski space, combining three-dimensional Euclidean space with time into a four-dimensional manifold, later extended in its applicability by his former student Albert Einstein in the theory of special relativity.

Enter David Hilbert (1895–1930)

Then, starting 100 years after Gauss’ arrival, Göttingen again experienced a surge in its prominence as a worldwide research institution. The presence of Klein and later arrival of David Hilbert (1862–1943) had attracted a new generation of promising doctoral students. Hilbert, by now known as one of the most influential and important mathematicians in history, joined Göttingen’s faculty in 1895 as the result of intervention on his behalf by his friend Felix Klein.

Hilbert is celebrated now for a wide variety of mathematical achievements, including his basis theorem, his axioms, his problems, and not least of all, his concept of Hilbert spaces, generalizing the notion of Euclidean space. This however barely scratches the surface of his contributions to mathematics and physics. He also worked on the general theory of relativity, proposing the action — now known as Einstein-Hilbert action — which yields the Einstein field equations through the principle of least action. When Hilbert solved Gordan’s problem, Paul Gordan, then-editor of Mathematische Annalen rejected Hilbert’s article, criticizing his exposition because it was insufficiently comprehensive, stating “Das ist nicht Mathematik. Das ist Theologie” (“This is not mathematics. This is theology”). Again, Hilbert’s colleague and friend Felix Klein came to his rescue, guaranteeing that Hilbert’s paper would be published without changes, writing him saying that:

“Without doubt this is the most important work on general algebra that the Annalen has ever published”.

Among Hilbert’s 69 Ph.D. candidates (!!) at Göttingen early on were Felix Bernstein (1878–1956) who proved the Schröder-Bernstein theorem in set theory and Hermann Weyl (1885–1955) known as one of the first professors at the Institute for Advanced Study and a highly influential mathematician who worked in logic, symmetry, topology and linear algebra. In addition, Hilbert supervised the dissertation of Polish mathematician Hugo Steinhaus (1887–1972) who would go on to publish more than 170 papers, including in geometry, probability, analysis, trigonometry, Fourier series and logic. Steinhaus is also noted as one of the early founders of game theory, having preceded John von Neumann’s more complete treatment Zur Theorie der Gesellschaftsspiele (“On the Theory of Games of Strategy”) by a few years.

Enter Max Born (1904–1933)

Physicist Max Born (1882–1970) first arrived in Göttingen in 1904, where he discovered Klein, Hilbert and Minkowski, forming close ties with the latter two and writing his habilitation thesis with Minkowki on the Thomson model of the atom. Hilbert however also immediately identified Born’s extraordinary abilities and appointed him to be the lecture scribe (the person who writes up class notes from each lecture). From this initial relationship, Born grew close to Hilbert, who became his mentor. Known primarily for his involvement in the development of early quantum mechanics alongside Werner Heisenberg and Wolfgang Pauli in the mid-1920s, Born also contributed to solid-state physics and optics, as well as supervise the doctoral dissertations of numerous notable Ph.D. candidates. He was awarded the Nobel Prize in Physics in 1954 for his contributions to the formulation of quantum mechanics, and in particular, his statistical interpretation of the wave function.

Otto Hahn (1879–1968), the eventual discoverer of nuclear fission, in 1906 assumed work with Emil Fischer (1852–1919) at the university of Berlin, working on radioactivity. Although never a faculty member at Göttingen, Hahn collaborated with numerous physicists at the university over the course of his career and upon his death in 1968 was buried in the city. Erwin Schrödinger (1887–1961), who eventually succeeded Max Planck’s professorship at the University of Berlin in 1926, similarly did not attend or work at Göttingen, but collaborated with many Göttingen physicists.

The father of quantum mechanics Werner Heisenberg (1901–1976) arrived to study physics with Born and mathematics with Hilbert at Göttingen in 1920. In 1922, during the “Bohr festival” at Göttingen in 1922, Heisenberg first met Niels Bohr (1885–1962), which had a significant and continued effect on him. Following his doctorate written under Arnold Sommerfeld (1868–1951) at the University of Munich in 1923, Heisenberg completed his habilitation in 1924 with a thesis on the Zeeman effect under Born. Heisenberg remained at Göttingen from 1924 to 1927 as a Privatdozent, except for a brief stay with Bohr in Copenhagen in the academic year 1924–25. His monumental paper Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen (“Quantum theoretical re-interpretation of kinematic and mechanical relations”), was published while in Göttingen in 1925. Heisenberg went on to win the 1932 Nobel Prize in Physics for the work.

Heisenberg’s collaborator Wolfgang Pauli (1900–1958) spent a year assisting for Born in Göttingen around the same time (1925–27). Pauli, who Heisenberg had been in correspondence with while writing his 1925 paper, later used it to derive the observed spectrum of the hydrogen atom in his paper Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik (“On the Hydrogen Spectrum from the Standpoint of the new Quantum Mechanics”) and so provide the first validation of Heisenberg’s theory. Pauli would also go on to be awarded the Nobel Prize in Physics, albeit not until 1945 at the nomination of Albert Einstein.

Pascual Jordan (1902–1980) was also part of the group of mathematical physicists who contributed to the early development of quantum mechanics in the 1920s. Arriving in 1923 from the University of Hannover, Pascual also worked under Born, as well as Richard Courant (1888–1972), then on the mathematics faculty. Another later Nobel laureate, Paul Dirac (1902–1984) was also there, having come from Cambridge in 1926. Dirac of course, was instrumental in the early development of both quantum mechanics and quantum electrodynamics, sharing the 1933 Nobel Prize with Schrödinger for “the discovery of new productive forms of atomic theory”.

The father of the atomic bomb, J. Robert Oppenheimer (1904–1967) also left his studies at Cambridge for Göttingen in 1926, to study quantum physics under Born. As did Enrico Fermi (1901–1954), most notable for the invention of the first nuclear reactor and for extending the work of Pauli by applying the principle of an ideal gas and employing a statistical formulation now known as Fermi-Dirac statistics. He was awarded the Nobel Prize in Physics in 1938 for his work on induced radioactivity by neutron bombardment and his discovery of transuranium elements. Similarly, Edward Teller (1908–2003), the “father of the hydrogen bomb” came to Göttingen in 1930 to study under Born, but eventually had to leave due to the rise of antisemitism in Germany. Another “Martian”, John von Neumann (1903–1957) came to Göttingen the same year as Oppenheimer did, in 1926. Unlike Oppenheimer, von Neumann went there for the same reason as Born did, to study mathematics under Hilbert. Having studied with Weyl at ETH Zurich, von Neumann travelled to Göttingen to work on Hilbert’s program of formalism and set theory, which he did, in addition to helping formalize several results in quantum mechanics. von Neumann remained at Göttingen until 1930 when he accepted a post as a visiting professor at Princeton University.

As von Neumann’s tenure in America came to an end, Adolf Hitler first came to power in Germany. Disgusted, this lead von Neumann to abandon his academic posts in Europe altogether, stating about the Nazi regime that

“If these boys continue for two more years, they will ruin German science for a generation — at least”

Following the Nazi crackdown on “Jewish physics”, current and former faculty at Göttingen including Born, Franck, Wigner, Szilárd, Teller, Landau and Courant in 1933 all fled the country. When in 1934 asked by the Nazi minister of education “How mathematics is going at Göttingen, now that it is free from the Jewish influence?”, Hilbert, still at his post, is said to simply have replied:

“There is no mathematics in Göttingen anymore.”