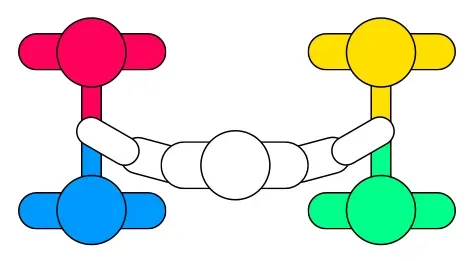
One of the more memorable and quotable scenes from the hit HBO show Silicon Valley occurs in the season 1 finale when the guys are debating “hypothetically” just how long it would take the founder of *Aviato*, Erlich Bachman to ehm, stimulate, an 800 man crowd to completion using only his hands. Panicked about how they are going to win Techcrunch Startup Battlefield the next morning, the guys go on to derive the beginnings of a sophisticated mathematical model considering the most relevant variables influencing the scenario where a (very) single individual has to stimulate 800 men to completion within 10 minutes:

The purpose of this article is to bring their work …to completion. My model builds on the work of Misra (2014). Happy reading!

“We’re gonna win even if I have to go into the auditorium and personally jerk off every guy in the audience!” — Erlich Bachman

The Model

Again, hypothetically, let us first consider the isolated stimulation of a generic individual i by an agent E (Erlich). Our model accounts for a perfectly cylindrical shaft of some girth D which is rigid. The area of contact between agent E and the circumference of the shaft of individual i is given by f(s) ∈ [0,1] where f(s) = 1 indicates that the agent is in contact with the entire circumference of audience member i’s shaft (Misra, 2014).

Stimulation

Each jerk is assumed to provide some amount of stimulation to individual i. That is, every jerk performed by agent E transfers a finite fraction of satisfaction S(f)T(f) ∈ [0,1] to the audience member, where S(f) and T(f) are spatial and temporal stimulation functions, respectively. The cumulative satisfaction after J jerks is hence given by

Written to solve for satisfaction per jerk:

For a ‘satisfaction event’ to occur, the cumulative satisfaction function must exceed each individual’s satisfaction event threshold Λ ∈ R⁺. When this occurs, the agent moves on to stimulate another member of the audience. In other words, for agent E to move on the following inequality has to be fulfilled:

Properties of the stimulation functions S(f) and T(f) are:

• In the absence of hand-on-shaft contact f(s) = 0, no stimulation can occur, as S(0) = 0 and T(0) = 0. This is also assumed to be the initial condition for each individual audience member i;
• Satisfaction is assumed to increase monotonically with hand-on-shaft contact, i.e. maximum satisfaction occurs at full spatial contact S(1) = 1 andfull temporal contact T(1) = 1 (full contact with audience member i for the duration of the stimulation).
• The temporal stimulation function is assumed to be a downward facing concave function ⋂, as hand-on-shaft contact is subject to diminishing returns.

There are 800 male audience members to be stimulated and a global time limit imposed by the duration of the team’s stage time, Tmax = 10 min. The resulting stimulation from each jerk is assumed to depend only on mechanical parameters. As Misra (2014) writes “a 20 year old man who hasn’t been stimulated in a week’s time receives the same gratification from a jerk action as would a freshly stimulated 80 year-old-man, provided the geometric parameters are identical”; For simplicity sake, we assume that shaft lengths follow a Gaussian distribution. Non-geometric variation between individuals is captured separately via an individual-level stimulation threshold Λ ∈ R⁺ (Misra, 2014).

In its most simple form, if the agent jerks faster, he is assumed to perform better. To control for this variance, instead of measuring the time spent on each individual, the relevant measurement for performance should be ‘number of jerks performed’. Assume that stimulation per jerk is a value ranging from 0 to 1, determined entirely by the fraction f(s) of an individual’s shaft that is in contact with the agent’s hand, and the time f(s) during a jerk action that contact is maintained. Assume that each individual has a rigid shaft and at t = 0 in its equilibrium position of perpendicular to the person’s body. Assume also that each individual’s shaft is flexible along the y-axis up and down by some shaft angle θ.

Sorting

In quadruple configurations, we assume that the audience is pre-sorted before the stimulation session begins, so that at t = 0 every individual is matched with another individual of the audience according to their so-called dick-to-floor ratio“D2F”, (less humorously) known simply as “leg length”. Let D2Fᵢ represent the distance from the floor to each individual i’s shaft when in the equilibrium position such that the shaft angle θ is equal to 0°. Next, sort the set of individuals in the audience by values of D2F from low to high and assign the first individuals in the set D2F₁, D2F₂, … to those with the shortest D2F. Next pairwise match individuals according to their dick-to-floor ratio D2F₁, D2F₂, such that you obtain a set of 400 objects S = {D2F₁, D2F₂}, {D2F₃, D2F₄}, … {D2Fᵢ, D2Fⱼ} which is sorted.

An alternative sorting parameter might have been girth similarity. If we let radii rrepresent the distance from the center of each dick to its perimeter. Sort the audience by values of r from low to high, such that r₁ is the dick with the smallest radius, and r₈₀₀ the member with the largest radius, r₁, r₂, …, r₈₀₀. Next pairwise match audience members starting with those with the lowest values of r, {r₁, r₂}, {r₃, r₄} and so on such that you obtain a new set containing 400 pairs sorted by girth similarity. Although this sorting would maximize the area of contact between agent E’s hand and each individual’s dick in the so-called shaft-to-shaft configuration (see below), it would lead to mechanical challenges in other arrangements (namely, in the tip-to-tip configuration) and so should be considered less optimal.

The shaft angle θ

Sorting by D2F minimizes the shaft angle θ (defined as the angle of displacement of each individual’s shaft from its equilibrium angle θ = 0°) for both individuals. However, to ensure accurate optimization when evaluating different configuration and strategies, one still needs to account for the diminishment of satisfaction-per-jerk stemming from this additional factor.

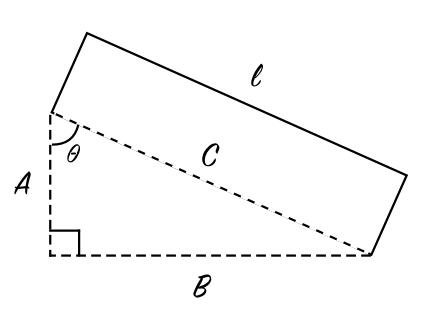
Let l equal the hypothenuse C of a right-angled triangle, where A and B are the short and long legs, respectively. Then θ ≠ 0° is the angle AC and the relationship between the length of the individual’s shaft and his shaft angle given by:

For the sake of simplicity , let us hence assume that the penalty due to loss of satisfaction-per-jerk stemming from the deviation in shaft angle is cos θ.

Strategies

Given the model outlined above, we may now proceed to define strategies for agent E generating 800 satisfaction events in 10 minutes, i.e. minimize the sum

subject to the time constraint Tmax = 600s, where J represents the number of jerks and S(f) and T(f) are the respective spatial and temporal stimulation functions of f(s), the area of contact between agent E’s hand and the shaft of individual i.

Single jerk strategies (SJ)

First, let us consider the case where agent E stimulates each audience member one by one in isolation. In such as scenario, having two hands, we assume agent E stands to maximize both factors in the satisfaction-per-jerk equation S(f)T(f), that both factors approach their maximum stimulation potential:

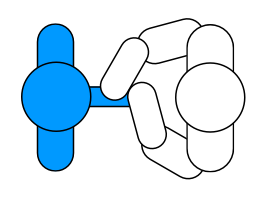
Double jerk strategies (DJ)

Although potentially decreasing the fraction of stimulation per jerk in the spatial dimension S(f), we still assume that agent E is able to grasp each shaft such that f(s) → 1. Doubling the number of audience members being stimulated simultaneously is hence assumed to be more efficient by approximately a factor of two.

In such a strategy, which does not require sorting by D2F ratio ahead of time, agent E would position himself on either side of the two individuals facing the same way and use both hands in a cross-country skate skiing motion, as shown below:

Quadruple jerk strategies

“Like two shake-weights” — Bertram Gilfoyle

Attempting to further increase efficiency, let us next assume that quadruple jerk strategies exist, such that agent E can increase the number of individuals being satisfied simultaneously, though at the cost of spatial and temporal satisfaction per jerk, S(f) and T(f), respectively. Among such strategies, two configurations seem most viable:

• “Tip-to-tip” jerking (TTJ): Agent E simultaneously stimulates four audience members in a series, organized end-to-end. This would presumably maximize area of contact between the agent and the shafts of the individuals being jerked f(s), at a cost of decreasing temporal stimulation T(f), as the length of movement for each jerk increases by a mean factor of two (L = l₁ + l₂). In the configuration used for such as strategy, audience members would line up “tip-to-tip” as shown below:

• “Shaft-to-shaft” jerking (SSJ): Agent E simultaneously satisfies four audience members in parallel, organized side-to-side. This would presumably maximize the temporal satisfaction function T(f), as unlike tip-to-tip there is hand-to-shaft contact of both individuals at all times. This is however at the cost of decreasing the spatial satisfaction function S(f), because the area of contact between the agent’s hand and each of the four shafts, f(s) < 1:

Efficiency

The necessary variable to evaluate the relative performance of each configuration, as Dinesh points out, should be mean jerk time μ. For a single jerk strategy SJ, mean jerk time would simply be given by:

For the double configuration DJ, “it doesn’t matter, but hypothetically, mean jerk time is equal to 400 total jerks at a two dick rate”:

Similarly, for the two quadruple configurations TT and SS where four members are being stimulated, the comparable mean jerk time will similarly be given by:

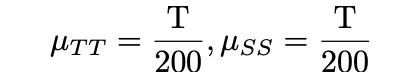
Evaluation

In order to evaluate the efficiency of each strategy, we will next consider the values of the spatial and temporal functions which map the contact area f(s) to the length of the shaft of each individual. For each strategy, we need to evaluate:

• f(s) ∈ [0,1], the area of contact between the hand of agent E and the circumference of the shaft of individual i;
• S(f), the spatial stimulation function that maps the area of contact f(s) along the shaft of individual i;
• T(f), the temporal stimulation function that maps the area of contact f(s) over the duration of the stimulation individual i;
• θ, the shaft angle;

Strategy A: “Focus”

The one-person stimulation configuration is fairly simply to evaluate. As stated before, we must here assume that agent E is able to maintain full contact with the shaft of individual i, and so that for the duration of the stimulation f(s) = 1, and so S(1) = 1 and T(1) = 1. We also assume that agent E is able to maintain the shaft angle θ in its equilibrium position until he exceeds each individual’s satisfaction event threshold Λ.

Solving for satisfaction per jerk (eq. 2), we obtain S(1) × T(t) = 1. Hence, each jerk transfers an amount of satisfaction equal to 1, and the number of jerks J simply have to exceed each individual’s satisfaction threshold (given in number of jerks):

Strategy B: “Skiing”

The two-person stimulation configuration is the only multi-jerk configuration where satisfaction-per-jerk is assumed to be unaffected by deviations from the equilibrium position of members’ shaft angles. This because as in the single jerk configuration θ remains zero throughout each simulation, a consequence of not having to be matched against the complementary shaft angle of another individual in series or parallel.

As such, we can again solve solve for satisfaction per jerk (eq. 2). Again, we obtain S(1) x T(1) = 1 and assume that each jerk transfers an amount of satisfaction equal to 1, and the number of jerks J simply have to exceed each individual’s satisfaction threshold (given in number of jerks):

Strategy C: “Tip-to-tip”

The “tip-to-tip” strategy TTJ, where agent E stimulates audience members in a serial configuration, the crucial satisfaction-per-jerk measurement is for individual 1 and 2, respectively, given by the equations:

where the cos/sin terms represent the diminishment in stimulation stemming from shaft angle deviation from equilibrium. Solving for satisfaction per jerk (eq. 2), we again assume that agent E is able to maintain full contact with the shaft of individuals i, j, k and l through the duration of the stimulation, but that on average, he is only transferring satisfaction to each individual half the time (since stroke length = shaft length, L = lᵢ + lⱼ). So, S(1) = 1 and T(1/2) = 1/2 gives :

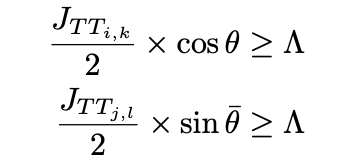
Strategy D: “Shaft-to-shaft”

In one sense, the “shaft-to-shaft” strategy SSJ is similar to the other quadruple jerk strategy “tip-to-tip” in that it requires us to incorporate terms for diminishment of satisfaction per jerk due to shaft angle deviation from equilibrium:

In another sense, the “shaft-to-shaft” configuration is the opposite of the other quadruple jerk strategy in that here we here assume that the agent is able to maintain contact with all individuals’ shafts throughout the stimulation. So, here T(1) = 1, but S(1) < 1 is assumed to be less than one due to the configuration of shafts side-by-side. We estimate that the inputs into f(s) would be equal to πr for the individual with the most girth Dᵢ, and range from [πrⱼ / 2 to πrⱼ] for the individual with least girth Dⱼ, as seen below:

Given this, solving for satisfaction per jerk (eq. 2) we obtain for individuals i, k:Sᵢ(πrᵢ) = 1/2:

and for individuals j,l: Sⱼ(πrⱼ/2) = 1/ 4 to Sⱼ(πrⱼ) = 1/2:

Thus, if Dᵢ = Dⱼ, the area of contact between agent E’s hand and the shafts of individuals i and j is the same and S(πr) = 1/2.

Hypothetical scenario

Finally, let us consider a hypothetical scenario and solve for number of jerks numerically, with the goal of coming up with an estimate of which strategy will be the most efficient given n = 800 guys and Tmax = 10 min.

Let the mean satisfaction threshold of an audience member be Λ = 100 strokes. Assume that the audience is sorted by D2F and so the mean shaft angle θ is 60°. Let the complementary shaft angle (bar theta) be given by β and equal 90°-60° = 30°. For the shaft-to-shaft strategy, assume mean girths of individuals i,k to be r = 1 and individuals j,l to be r = 2. Given this mismatch, it is fair to assume that f(s) = 1/4 for shafts j and l. We can now easily obtain the number of strokes required to achieve satisfaction events, by their respective inequalities:

Single jerk: J ≥ Λ
Double jerk: J ≥ Λ
Tip-to-tip i,l: J x 1/2 x cos(θ) ≥ Λ
Tip-to-tip j,k: J x 1/2 x sin(β) ≥ Λ
Shaft-to-shaft i,l: J x πr x 1/2 x cos(θ) ≥ Λ
Shaft to shaft j,k: J x πr x sin(β) ≥ Λ

Satisfaction per jerk
We immediately notice that single and double jerk strategies are equally as efficient on a per individual basis, such that the number of jerks required is equal to the satisfaction threshold Λ = 100.

For the tip-to-tip strategy, we obtain J x 1/2 x 1/2 = J x 1/4 for both individuals in each pair, telling us that per jerk the strategy is 25% as efficient as single and double jerk strategies given shaft angles of 60° for individual i,l and complementary shaft angles of 30° for individuals j,k. As such, a mean number of strokes J = 400 will be necessary to exceed the satisfaction threshold of Λ = 100.

For the shaft-to-shaft strategy, we obtain J x 1/4 for individuals i,k and J x 1/2 for individuals j,l. Compared to the tip-to-tip strategy, we observe that for individuals i,k the strategy is half as efficient (12.5%), and for individuals j,l equally as efficient (25%).

Satisfaction of the whole crowd
Common parameters to all jerking sessions is n = 800 guys, the time constraint of Tmax = 600s and the mean satisfaction threshold of 100 jerks:For the single jerk strategy, agent E has 600s to jerk 800 guys 100 times, requiring a rate of (800 x 100) / 600 = 133.33 jerks per second.

For the double jerk strategy, agent E has 600s to jerk 400 guys 100 times, requiring a rate of (400 x 100) / 600 = 66.67 jerks per second.

For the tip-to-tip strategy, agent E has 600s to jerk 200 guys 400 times, requiring a rate of (200 x 400) / 600 = 133.33 jerks per second.

For the shaft-to-shaft strategy, agent E has 600s to jerk 200 guys (600 + 400)/2 times, requiring a rate of (200 x 500) / 600 = 166.67 jerks per second.

Conclusion

In conclusion, we’ve found that of the four strategies evaluated (‘focus’, ‘skiing’, ‘tip-to-tip’ and ‘shaft-to-shaft’), given reasonable assumptions and parameters, agent E should go for the double jerk (“skiing”) strategy which is evaluated to be twice as efficient as single jerk and tip-to-tip strategies.

I encourage everyone interested to read the original paper “Optimal Tip-to-Tip Efficiency” by Misra (2014), which this essay was based on.