Once the door for studying light was opened with Maxwell-equations, physics, instead of move ahead further, was nearly collapse under the weight of the past. Experiments made to tell the Earth’s absolute speed through the hypothetical aether did not show anything besides incorrectness. Maybe I am overreacting a little with those black clouds gathered in the sky; nonetheless, physics was in a corner — harmony disturbed was demanded to return.

The Michelson-Morley and other experiments show that the principle of relativity is obeyed by light what stayed in contradiction with assumptions made by following the Galilean-Newtonian transformation: Times for the perpendicular and parallel parts must equal. The only possibility that the beams could have reached the detector at the same time is their equality. If so, a hypothesis that the space is absolute must be wrong.

For this, something strange must happen to the moving apparatus; namely, either:

• the perpendicular part elongates to take more time, adjusting to the longer parallel time,
• the parallel part foreshortens to take less time, adapting to the shorter perpendicular one,
• or something in-between.

Shortly, from all options, the idea of foreshortening fits later observations, meaning, is correct. At least up-to-date.

How much the parallel-to-motion part foreshortens?

For being calculated, times of both paths must get equated, and the parallel length, L, must be multiplied by k, which, when computed, tells how large the foreshortens effect must be.

That is:

What gives:

Then,

it is the factor about which the parallel length must get contracted.

Time dilatation

Time, a concept that directly or indirectly exists but to which man has no understanding, about which cannot tell what it can be. Does it have either a particle, wave, or else nature? Whatever it is, one is sure: it determines the dynamics of the Universe. Without it, everything would be like objects in a picture: not-moving, freeze, and unable to change; another story that those objects would not even be there. Everything would be dead — huh; if death would have even existed. It is not a farouche accident that it appears in all derivatives of motions. Motion is life, but it depends on time. Anyway, what man indeed does now is how to measure time.

At this point, one thing you should know and remember, when you either move with constant velocity or not move at all, the principle of relativity holds for you. Thus any known phenomenon that you would think could permit you to determine which system you are in will not give you any hint. Here and there, physics is invariant, stays the same. In particular, measuring time, whatever a clock is used by you when being inside a system, your time-rate flow cannot change. Otherwise, you would have been able to use this mismatch to determine whether you move or not; and if yes, then how fast. It would violate the principle of relativity. So, whatever a clock, you cannot see any difference in measuring time.

But.

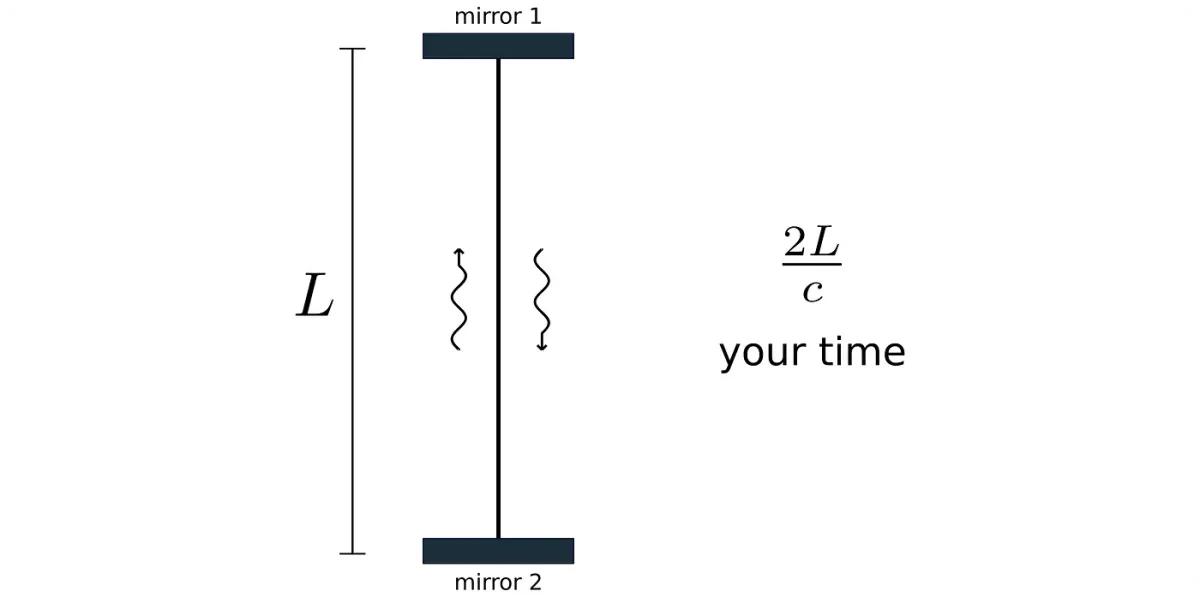
Someone at rest can watch you as you are moving (of course, from your perspective, you would have an equal right to state that he is moving and you are stationary,) observing how bizarre your clock behaves. Imagine a silly clock that measures time by light going between two parallel mirrors separated by a length, L (like the perpendicular arm from the Michelson-Morley experiment apparatus,) and that this observer sees you as moving with a velocity, v, along his x-axis. For you, nothing strange happens as the light goes up and down, covering a distance of 2L between neighboring announces of an elapsing time.

However, how he perceives this silly motion?

The mirrors are situated perpendicularly to the velocity v, so he does not notice any contraction of the arm’s length. In other words, it is L as well. But as the light moves between the mirrors, it must cover not only L distance but one given by the apparatus motion as well. So it takes the zigzag path.

Meaning any of your actions looks like being slowed down for someone watching you by:

Time dilatation was confirmed by taking two synchronized atomic clocks and positioning them in motion relative to each other; namely, one was left on the ground, here on Earth, whereby the second take a plane flight. When compared, they had no longer matched.

The transformation

Once being well-equipped, this story can get to its point.

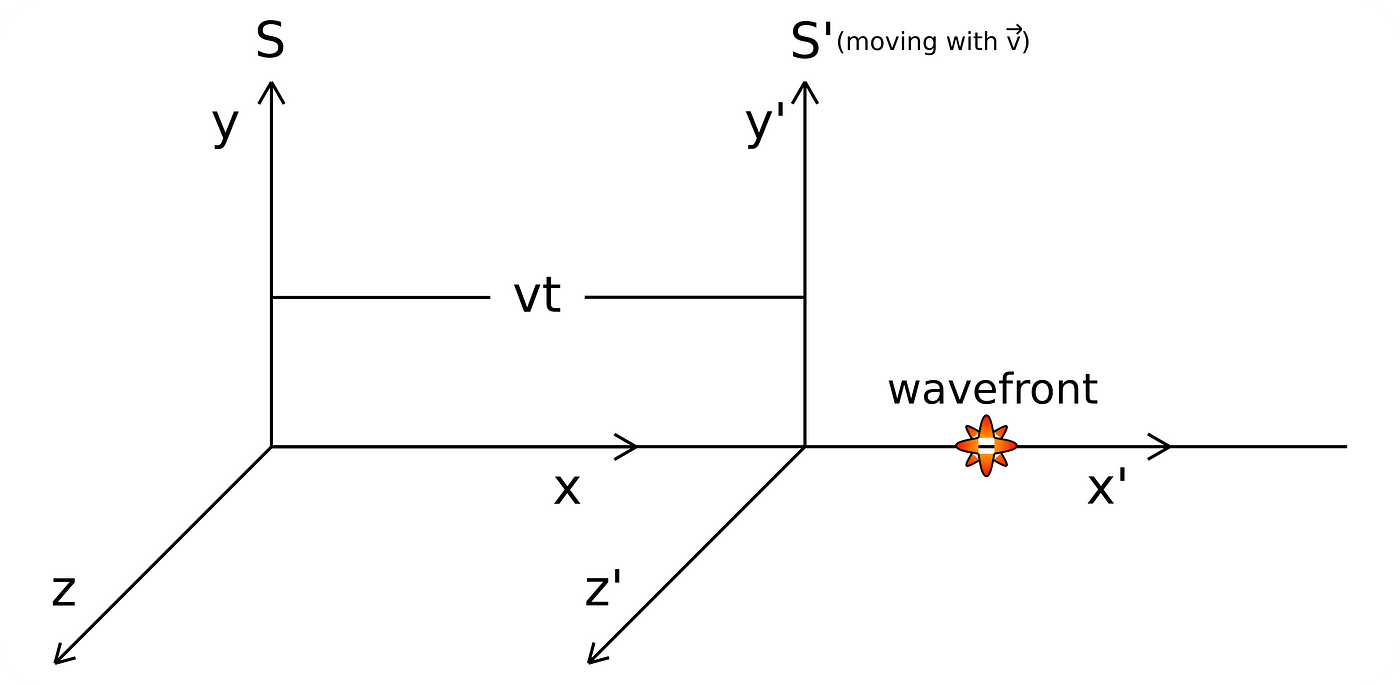
Let’s take two reference frames, S and S’ moving relative to each other. Whereby S is stationary and S’ moves relative to it. Again, this situation is reversible since the S’ has an equal right to state that he is at rest — then it would be inverse Lorentz-transformation. Nevertheless, for us, S is fixed. In other words, we observe S’ from S. Note:

• S(x, y, z, t)
• S’(x’, y’, z’, t’)

Assume that both initially coincide and that S’ as seen by us moves with a velocity v.

The transformation is alike:

In any reference frame, a linear motion may always align along any of its axes by rotation. Physics does not depend on how you orient your coordinates; it would be critical if it would. That is why z’=z and y’=y.

Length transformation

Imagine that S’ is a ship and that someone inside wants to measure the distance between its ends: he strives to know how long it is. It so happens that the direction he has chosen coincides with our x-axis, along which the ship moves. So, he takes a meter stick and lies it down n times; once he finishes, he believes (and has full rights to do so) that the distance measured is one-to-one with the meter definition. Namely, x’.

But.

For us, during all time, he has been using the meter stick that was foreshortened by:

Thus as seen by us:

Adding to it the separation due to the ship motion, vt:

Finally, by rearranging terms:

Time transformation

To relate times, imagine an artificial event occurring at the moment of the S and S’ coincidence, at the start, that spreads out as a spherical wave with the speed of light: it might be just a shining bulb. After time t, the wavefront of light the bulb has produced is at the position (x, 0, 0, t) and (x’, 0, 0, t’), respectively, as seen by both men.

What are their position vectors (from their origins) to the wavefront?

Simply:

Thus:

y, z, y’, z’ are 0, so let’s remove them:

By the assumption that the speed of light is invariant for all inertial reference frames — it has to be; otherwise, the principle of relativity would not hold:

Hence:

Substituting for x’:

Multiplying by t/x:

Substituting x/c for the numerator’s subtrahend t and factoring out x:

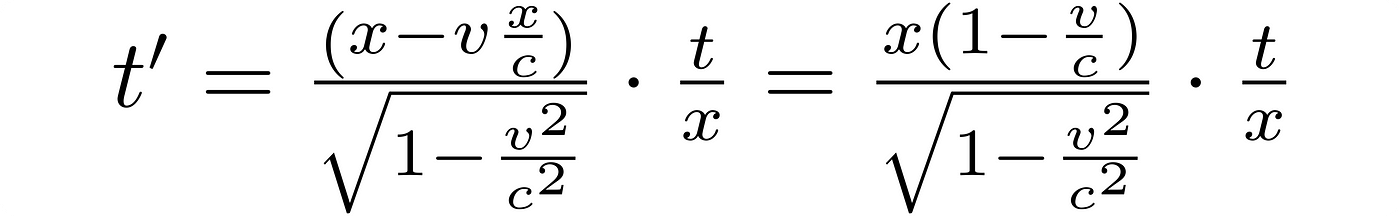
Crossing out x and multiplying the numerator by t:

By substituting x/c for t in the numerator’s subtrahend:

By rearranging the subtrahend:

it finally appears as it stands in the Lorentz transformation.