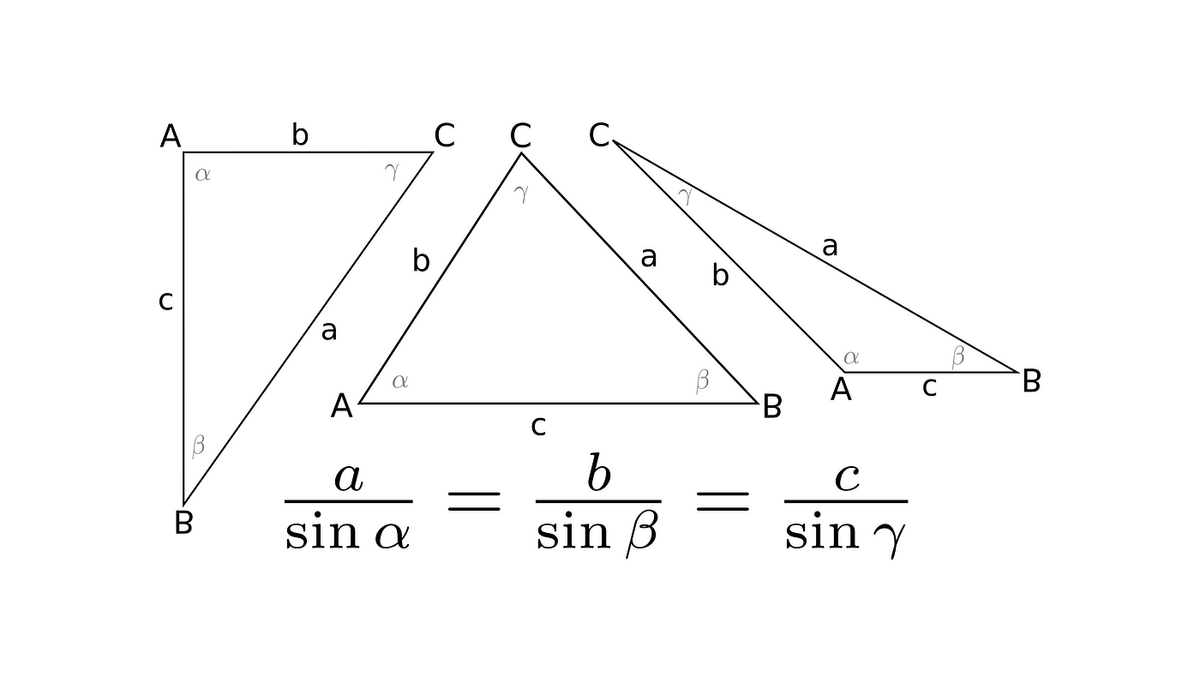
Each triangle belongs to one of three groups about which membership its angles decide. These are the right, acute, and obtuse triangles. The law of sines holds within them all.

Right triangles

There is a right-angled triangle with the vertices A, B, C at which angles are α, β, γ, where α is the right angle. Lowercase a, b, c are the lengths of the sides that opposite vertices marked with the same, but uppercase, letters. I will repeat this scheme for all the other cases. So, keep it in mind for faster catching what is going on within the next problems.

The question, how to compute the area of a triangle?

It is quite simple. Just multiply any of its sides times the corresponding altitude and divide it by 2. Notice also that two altitudes are catheti while one is not. We should start by adding this one to our picture.

How to compute h?

Altitudes always form right angles with providing them sides. So, we have two the right-angles triangles using which we could compute h by the sine function.

Let us do it for both of them,

computing the area of the ABC triangle using both of the above notations for h, plus one more (we want to have sine for all the angles,) thus:

What are we trying to prove?

That, all ratios of a side to the opposite sine are equal.

If that so, a side should stay inversely with sin90°, b with sinβ, and c with sinγ.

What must be done to make it happen?

By looking at the above equation, it is clear that each part of this equation needs what it misses. So, all these terms must be multiplied by 2/abc.

And, by taking its reciprocal,

the law of sine appears in the known form.

Acute triangles

Comparing this triangle with the right one, its angles are lower than 90°. But, it does not change the logic behind the proof. There is still a necessity to tight the sines up to their opposite sides. To do so, 3-different expressions of its area are needed that will involve these sines.

So, what to start with?

As with the earlier case, we need any two of its altitudes to make a dish.

Nothing more left than to express its area with these altitudes.

And, for the same reason, it has to be multiplied by 2/abc. Once done,

the dish is cooked.

Obtuse triangles

Pretty much everything is the same as before. The whole procedure goes the same way. But, yes there is a but.

Where are altitudes of obtuse triangles defined?

Only one of them is inside, while two go on the outside. But we need two…

How to bite it?

That is where the sine’s supplementary angle identity comes in handy. You can read about it in my earlier story, just here.

And, it is the solution to the problem. Because whether an altitude is inside or outside makes no difference for the sine function. So let me now draw two.

After this, we could write down area equations.

However, sinα’=sinα, thus:

Now, multiplicating it by 2/abc and taking its reciprocal results with the law of sine.

Until next time!