There once lived a man named Marie Jean Antoine Nicolas de Caritat, Marquis of Condorcet (1743–1794). A mathematician and philosopher, his work was mainly focused on advancing social progress towards a more egalitarian society. For instance, he strongly advocated for gender equality as early as in 1787, when he wrote:

“The rights of men stem exclusively from the fact that they are sentient beings, capable of acquiring moral ideas and of reasoning upon them. Since women have the same qualities, they necessarily also have the same rights.”

Despite his best efforts, the majority of French society and indeed all the “enlightened” societies did not agree with Condorcet’s view about women’s suffrage in the 1700s. I was surprised to learn that it took more than 100 years before New Zealand became the first country to recognize women’s right to vote in parliamentary elections in 1893. For me, this begged the question

Why did it take so long for the majority of people in the world’s many countries to reach what is now considered such an obvious truth?

Although Condorcet worked in politics later on, he started out in scientific research. Indeed, from 1765–74 he focused exclusively on science, working with the likes of Leonard Euler and Benjamin Franklin. In 1785, he combined his passion for politics and science when he expressed a result now colloquially known as “the wisdom of crowds”, the Condorcet’s jury theorem, here described by Cass R. Sunstein in his 2006 essay When Crowds aren’t Wise:

Condorcet's Jury Theorem
Suppose that a number of people are answering the same question and that there are two possible answers, one correct and one incorrect. Assume, too, that the probability that each individual will answer correctly exceeds 50%. With a few calculations, the theorem shows that the probability that a majority of the group will answer correctly increases toward 100% as the size of the group increases.

Anyone who has ever played blackjack in Las Vegas knows the prediction of the theorem intuitively: If the house’s odds of winning each hand is 51%, then over time the house’s odds of winning more hands than you approaches 100%. However, Condorcet’s theorem teaches us more than just that. Indeed, I would argue, it helps us understand why objectively worse outcomes can occur in general elections and perhaps even why Condorcet’s goal of women’s suffrage took so long.

How Crowds Can Get it so Wrong

We know there is a city of 650,000 people in the middle of the Nevada desert because in the long run, the house always wins. The fact that the house always wins is the prediction of Condorcet’s theorem.

The Condorcet Jury Theorem
The more people you ask a question, the more likely it is that a majority of the answers you are given are correct, given three assumptions:a) It is a factual, binary, true-or-false question;
b) Each person has a greater than 50% chance of answer the question correctly;
c) Each person answers independently based on private information

Now examine the theorem’s properties. Pay close attention to the assumptions, because they make all the difference. In particular, look at assumption b): “Each person has a greater than 50% chance of answering the question correctly”. What if we break this assumption? Assume instead that each person has less than 50% chance of getting the question right. Let’s say their chance is 49%, 48%, or 47%. How does that change the prediction of the theorem? A graphical depiction:

Notice that indeed, the predictions of the theorem are symmetric about the 50% mark, depending on the variable p: what the probability of each voter selecting the good outcome is. Meaning, just as the good outcome occurs if each person has a greater than 50% chance of being right (if each game of black favors the house more than 50%), the bad outcome is equally likely to occur if each person has a greater than 50% chance of being wrong. The question then becomes:

How many people do we need to include in the group of voters to be certain that the good outcome occurs?

The Mathematics of Group Decisions

Formally, let us define a situation where:

A group wishes to reach a decision by majority vote. One of two outcomes of the vote is good, the other outcome is bad. Each voter has an independent probability P of voting for the good outcome.

Condorcet’s jury theorem asks how many voters we should include in the group in order to ensure that the majority chooses the good outcome. The result depends on whether P is greater than or less than 0.5 (50%):

• If P is greater than 0.5 (each voter is more likely to vote for the good outcome), then adding more voters increases the probability that the good outcome occurs. In the limit, the probability that the majority votes for the good outcome approaches 1 as the number of voters increases.
• If P is less than 0.5 (each voter is more likely to vote for the bad outcome), then adding more voters makes things worse: the optimal electorate consists of a single voter.

Let’s prove it:

Proof of Condorcet's Jury Theorem
To avoid the need for a tie-break, let us assume that the number of voters n is an odd number.Suppose we start with n voters and let m voters vote for the good outcome. Consider what happens to the vote when we add an additional two voters to the group. The majority vote can only change in two cases:1. m was one vote short of getting a majority of the n votes, but both new voters voted for the good outcome;
2. m was equal to a majority of the n votes, but both new voters voted for the bad outcome;In all the other cases the outcome does not change by the addition of two extra voters. Rather, instead a) The two votes cancel out, b) Increase the gap or c) Don't make enough of a difference. We thus only care about what happens when a single vote (among the first n votes) separates a good outcome from a bad outcome.Analyzing this case, imagine that the first n - 1 votes cancel out so that the deciding vote is cast by the nth voter. In this case, the probability of getting the good outcome is the same as the probability P that the nth voter will vote for the good outcome. Now suppose we add another two additional voters. The probability that the additional voters change a bad outcome to a good outcome is:(1 - P) × P × P = (1 - p)p²The probability that the additional voters change a good outcome to a bad outcome is:P × (1 - P) × (1 - P) = P(1 - P)²The first of probability is greater than the second if and only if P is greater than 0.5, proving the theorem.

The Role of Misinformation

So, did the lack of women’s suffrage stem from a majority decision among independent-minded men who agreed that women are somehow less equal than men? Unlikely. However, given that it took another 150 years (!!) for them to agree on women’s suffrage, it begs the question how the “wisdom of the crowd” favored the bad outcome for so long. Let’s revisit the assumptions of the theorem, this time around emphasizing assumption c) Each person answers independently based on private information.

In two dimensions (left/right, up/down), a group of people trying to agree on a good outcome is analogous to having 1000 people shoot an arrow at the bullseye of a target, and taking the mean position of all of their arrows to find what is likely the bullseye:

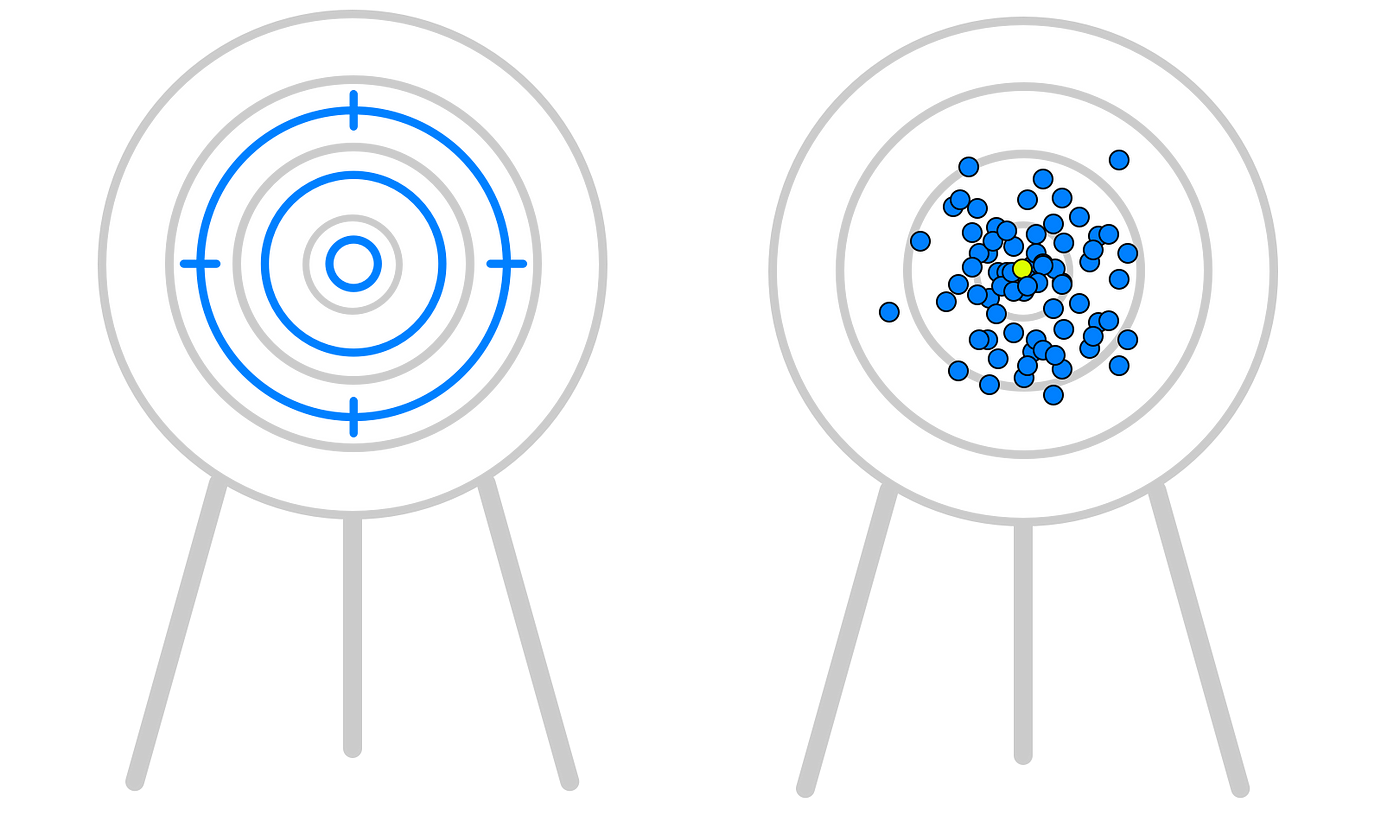
However, if we put vision-distorting glasses on all 1000 shooters which offsets their impression of where the bullseye is (slightly right, slightly down), the position of the mean arrow changes:

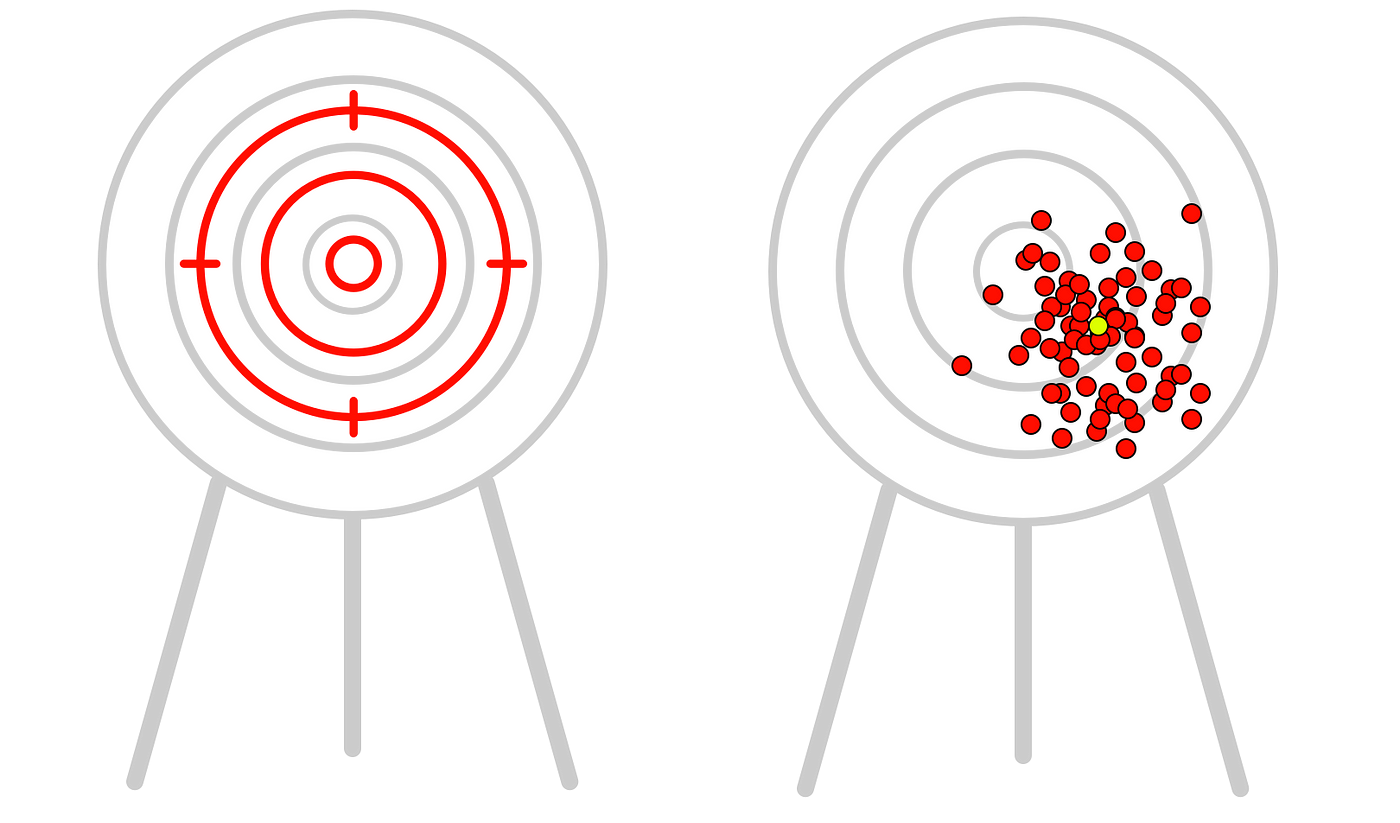
Although each shooter in both cases thinks they are aiming at the center of the bullseye (the good outcome, left in the figure above) they may in fact be aiming somewhere else (a worse outcome, right in the figure above). Vision-distorting glasses is an analogy for misinformation, in this case on a two-issue vote.

Epilogue

“Businesses and governments take heed: When there isn’t a lot of dispersed information within an organization, it’s ill-advised to rely on what its members think.”

Let us end on the note from legal scholar Cass R. Sunstein above. Although most of us may be more likely to vote for the good outcome, our ability to know whether or not we are aiming for the bullseye or not at all, is entirely dependent on the information we consume and what that information does to our aim.