The Intuition Behind Integration

Integral calculus and differential calculus are two sides of the same coin. Integration, however, can seem more complicated than differentiation because it involves the introduction of foreign notation and abstract ideas. However, the ideas themselves are beautifully intuitive and allow for the translation of complex ideas to simple algebraic manipulations. This article seeks to provide an intuitive view of integral calculus, showing how the math logically flows from the ideas and detailing the uses of integration.

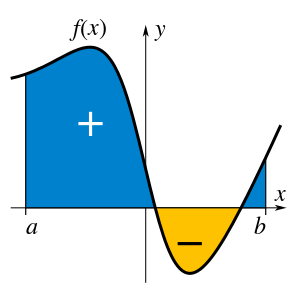
Classical integration really isn’t much more than calculating areas under curves. In middle school, we all learnt how to calculate the areas of various regular and irregular polygons. We also learnt the formulas for finding the area of a circle and ellipse. But how would you go about calculating the area of other curved shapes? What about finding the area under a curved function, such as the one below?

You’ll find that none of the methods you’ve learnt so far enable you to do so. This is where the prowess of integral calculus comes into play. As it turns out, however, calculating this area isn’t as difficult as it may seem, and the procedure is rooted in the more familiar methods.

So, how do we go about finding the area? What if we divided the region into more standard shapes — such as a rectangle. We know how to find the area for a rectangle — it's just the length x width. Let’s split the area into rectangles with an equal width which just comes under the curve. This looks like:

This is what our estimation would be with 4 rectangles. We can calculate the area of each of these rectangles since we know the width (the distance between the endpoints a and b divided by 4) and the height (the function evaluated at the right endpoint). Now, this clearly isn’t a very good estimation — look at all that space. But what would happen if instead of 4 rectangles, we used 10? Or 1,000? Or 100,000? What would happen if we let the widths of every rectangle approach 0 and the number of rectangles became closer and closer to infinity?

Well, then we would have the exact area. This makes sense intuitively: as the width of the rectangles becomes smaller and smaller, the individual rectangles fit the curve better and better; the sums of their areas converge to the true area between the curve and the x-axis. Here’s a nice animation illustrating this point:

This idea can be made rigorous by describing it mathematically:

This formula can look quite daunting at first, but all I’ve done is transcribe my exact words into mathematical notation. Let’s go through it piece by piece, working from the inside out. Inside the summation, we’re simply calculating the area of a rectangle by multiplying the value of the function at the right endpoint by the width of the rectangle, as described before. This width is given by the difference of the endpoints divided by the number of divisions (this ensures every width is equivalent). The actual integral can then be calculated via summing the areas of all of the rectangles as the number of rectangles approaches infinity.

This is describing only one kind of integral, however. It turns out that you don’t need to ensure the rectangles have an equal width nor do they need to have a height equivalent to the right endpoint. A more general representation of this formula is as follows (which is what you’re more likely to see), using standard calculus notation:

This is known as a Riemann Sum, after Bernhard Riemann, one of the founding fathers of complex analysis. Now, this looks even scarier, but we just added a few more details. What this formula states, quite plainly, is that you can calculate the area between a function and the x-axis as the sum of rectangles. The area of each rectangle is given by some arbitrary width, Δx, and the height is given by the value of the function of x, where x is chosen on some criteria (left-endpoint, midpoint, greatest value, etc.).

The above equation appears complex, but all it does is mathematically quantify what was previously stated. As the widths of the rectangles get infinitesimally small (closer and closer to 0), our approximations for the area using rectangles become more and more accurate. The equation generalizes an integral through the fact that the width does not have to be consistent and that the height of the rectangle can be determined via different criteria; the end integral, however, will always be the same.

The notation of an integral, ∫, is just an elongated S (standing for sum), and we are evaluating the integral of a function f(x) between 2 points: a and b. The dxsimply denotes an infinitesimal value for the width of each partition (this is the equivalent of Δx in our integral, as Δx tends towards 0).

An integral which is evaluated between 2 points is known as a definite integral. A definite integral allows us to actually calculate the area between a function and the x-axis (or the y-axis, or even another function, but that’s slightly more involved).

How is this integral actually evaluated? Luckily, you don’t have to go through a lengthy process of summing many, many rectangles. The first part of the fundamental theorem of calculus states that:

F(x) is standard notation for the antiderivative of f(x). What this means is that the derivative of F(x) is equal to f(x) i.e. F’(x) = f(x). Antidfferentiation is the process by which, given the derivative of a function, you ascertain the original function: if f’(x) = 2x, what was the original function we differentiated? The upshot is an indefinite integral returns a function; a definite integral returns a value. This is the secondary purpose of an integral: it is the inverse function of a derivative. This is shown mathematically by the second part of the fundamental theorem of calculus,

The above integral is an indefinite integral, as it has no endpoints. All this integral does is find the antiderivative of a function. In order to evaluate it, you must be familiar with differential calculus and the rules of derivatives. There are a variety of rules you can use to solve it, and they stem from how derivatives are computed.

Here are the basic rules. If you’re confused by this chart or don’t understand where these rules come from, I recommend that you further read up on derivatives (which are just as intuitive as integrals, if not more so).

So, in order to find the area between a function and the x-axis, you first perform antidifferentiation upon the function and then evaluate it at both endpoints (remember that the antiderivative is still a function). Finally, subtract the first result from the second as stated by the fundamental theorem.

So far this has all be very abstract and technical, so let’s actually apply the concepts in an example. We want to find the area of the function f(x) = 3x²between the endpoints 0 and 6. The first step is to find the antiderivative of this function. Antidifferntiating it, we get F(x) = x³ (using Rule №4 from the chart). If you want to double-check, simply take the derivative of F(x): if it equals f(x)i.e. the original function, its correct.

We know plug in the values for our endpoints into F(x). F(0) = 0³= 0 and F(6) = 6³ = 216. We now subtract F(0) from F(6): 216 − 0 = 216. ∴ The area between the graph of the function f(x) and the x-axis is 216 units². That wasn’t too difficult now, was it? Integration problems can and do get more complex, but the underlying principle of finding some value by summing smaller and smaller sections remains the same.

Integration is one of the most important techniques in math, with applications ranging from physics to finance. But it isn’t as complex or intimidating as people think — the underlying concepts are incredibly intuitive and comprehensible. In fact, you may naturally find yourself thinking in terms of integration for certain problems that appear unsolvable. The issue with calculus for most people lies in the algebra, but when you understand what the algebra truly represents, it becomes significantly less daunting and obfuscated.

Integral calculus is closely related to differential calculus, and all other branches (differential equations, vector calculus, multivariate calculus, etc.), stem from these two founding ideas. The goal of this article is to introduce the notion of integration, letting the math flow from the intuition. Integral calculus has allowed us to understand our world better and describe phenomena more precisely than we could ever have hoped.