From Newton’s “Lion Claws” to the Modern Solution

In June 1696, the renowned mathematician Johann Bernoulli published in the Acta Eruditorum, the first German scientific periodical, the following problem:

“Given in a vertical plane two points A and B, assign to the moving [body] M, the path AMB, by means of which — descending by its own weight and beginning to be moved [by gravity] from point A — it would arrive at the other point B in the shortest time.”

It can be expressed in a more straightforward way as:

“Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time.”

The figure below shows Johann Bernoulli (on the left) and the problem’s statement in the June 1696 Acta Eruditorum written in Latin (on the right).

This mathematical challenge is known as the problem of the brachistochrone. Even though Johann Bernoulli already knew how to solve it himself, he challenged other mathematicians in Europe and allowed six months for its solution. However, after that period, no answer was given. Even Gottfried Leibniz, one of the greatest intellects in history, requested an extension of the deadline. On the afternoon of January 29, 1697, Isaac Newton found the challenge in his mail (in a letter from Bernoulli). He then solved it during the night and sent the solution anonymously. When Bernoulli received it, he famously declared he recognized the mystery solver “tanquam ex ungue leonem,” which means “as the lion by its claw.”

On the afternoon of January 29, 1697, Isaac Newton found the challenge in his mail, solved it during the night and sent the solution anonymously. When Bernoulli received it, he famously declared he recognized the mystery solver “as the lion by its claw.”

Newton’s handwritten solution is shown below. As remarked here, “this story gives some idea of Newton’s power, since Johann Bernoulli took two weeks to solve it.”

The translation of Newton’s handwritten solution is:

“From the given point A draw the unbounded straight line APCZ parallel to the horizontal and upon this same line describe both any cycloid AQP whatever, meeting the straight line AB (drawn and, if need be, extended) in the point Q, and then another cycloid ADC whose base and height [as AC : AP] shall be to the previous one’s base and height respectively as AB to AQ. This most recent cycloid will then pass through the point B and be the curve in which a heavy body shall, under the force of its own weight, most swiftly reach the point B from the point A. As was to be found.”

To find Newton’s detailed explanation of the above solution, which was requested by the Scottish mathematician and astronomer David Gregory, check this link.

The Brachistochrone Curve

The brachistochrone, also called the curve of fastest descent, is a curve located on the two-dimensional plane, with some initial point A and a final, lower point B, on which a bead slides in the shortest possible time, due to the presence of a gravitational field.

The problem of finding the curve has the following assumptions:

• There is no friction in the curve
• The bead starts at rest
• The gravitational field is constant g

Modern Solution

Suppose the solution is the function y=y(x) where for convenience we choose the initial point to be A = (0,0). The final point is defined as B = (a, b). Since the bead is initially at rest, conservation of energy will give us:

We then write dt as:

The total time the bead takes to go from A = (0,0) to B = (a, b) is then:

The mathematical object T depends on the function y(x) and it is, therefore, called a functional (a function of a function). A function depends only on (one or more) variables, not on full functions.

The problem we want to solve is to find which function y(x) minimizes the total time T. For that, we will need to learn about the field of mathematics called calculus of variations.

Calculus of Variations

Consider a function ψ(x) which satisfies the conditions shown in the figure below, namely ψ(x₀)=y₀ and ψ(x₁)=y₁. Consider then a second function very close to the first one and write it as

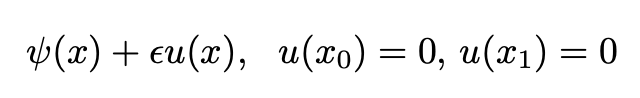
Note that for the conditions on ψ(x) to be obeyed, the above conditions on u(x) must be satisfied (for more details see Butkov).

Now consider the following functional:

Note that by varying L(x, y, y’), we obtain different values for the definite integral S[y(x)]. Now let us consider the variation of L as we vary ψ(x):

Integrating both sides, performing an integration by parts on the second term, and using the conditions obeyed by u(x), we obtain the following expression for the variation of the integral S:

For the omitted steps before Eq. 7 see Butkov. Now, if S is a minimum, δS=0 (as in common calculus). Since u(x) is arbitrary, we must have:

The expression inside the brackets vanishes when y(x) is equal to the function ψ(x) that makes L an extremum. Simplifying the notation we obtain the famous Euler-Lagrange equation:

Let us apply it to find the minimum time in Eq. 3 where:

(note that constants were omitted since they would cancel out). We obtain, after a few steps of algebra, the following differential equation, and its corresponding solution:

where k is some constant (dependent on boundary conditions) and the following change of variables was used:

These parametric equations describe a cycloid which is the curve that minimizes T as shown in the figure below.

Newton’s Solution

In 1699, the mathematician, natural philosopher, astronomer, inventor, and religious campaigner Nicolas Fatio de Duillier published the treatise “Double geometric research on the curve of the fastest descent” which included another solution to the brachistochrone problem.

David Gregory again asked Newton to simplify Fatio’s solution. The requested simplified version (which contained only twelve lines, excluding the incorrect lines which Newton crossed out, and it is shown below) of Fatio’s solution was sent by Newton to David Gregory in 1700. In this section, I will describe this solution, closely following the treatment in Roy.

In Fig. 10 the relevant quantities are defined. Following Newton we first write:

Now, we know from basic kinematics that the velocity of the falling bead at x is given by:

The time the bead takes to move along the ENG is proportional to:

Now defining:

Minimizing the total time t with respect to q, we obtain, after some simple algebra the differential equation of a cycloid, given by Eq. 11.

Thanks for reading and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin, personal website www.marcotavora.me, and Github have some other interesting content about math and physics and other topics such as machine learning, deep learning, finance, and much more! Check them out!