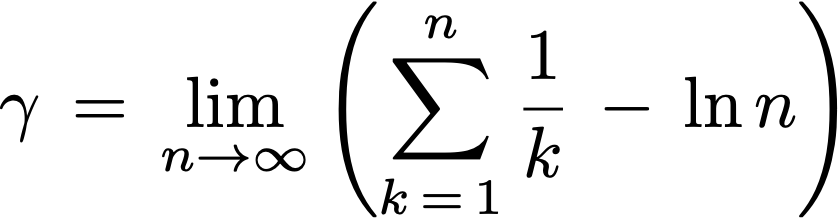
Remember the harmonic series?

More often than not, it serves as one’s first encounter with a series wherein individual terms diminish successively yet the series diverges to infinity. The below quote nicely sums the up notoriousness of the harmonic series:

Today I said to my calculus students, “I know, you’re looking at this series and you don’t see what I’m warning you about. You look and it and you think, ‘I trust this series. I would take candy from this series. I would get in a car with this series.’ But I’m going to warn you, this series is out to get you. Always remember: The harmonic series diverges. Never forget it.” — Source

Indeed. Never forget. The harmonic series diverges. Flirting continuously with convergence all the way, yet slowly but surely making its way to infinity. Increasing ever so slowly. In your grasp, yet out of it. Coldly tantalising its suitors.

By now, the series’ divergence has been confirmed via myriad different proofs, though none more beautiful than the very first one, which stands out for its simplicity. However, in this article, we would be concerned with the question

Is there any function which provides a decent approximation to the partial sums of the harmonic series?

Here, by partial sums, we mean the first n terms of the series, ie, -

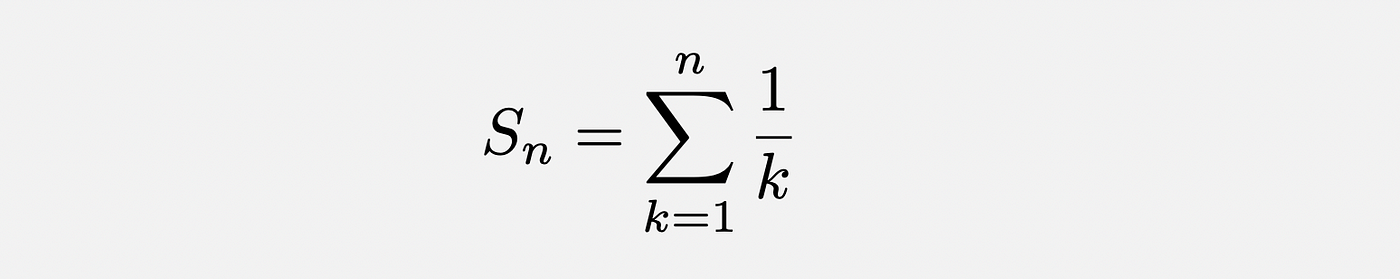
It turns out there is one, the natural logarithm function. As n gets larger, the difference between the partial sums and ln(n) approaches a finite limit. This limit is known as the Euler-Mascheroni constant, γ (gamma).

First appearing in 1734, the constant derives its name from two mathematicians — the ubiquitous Leonhard Euler, and Lorenzo Mascheroni, an Italian mathematician. The notation γ was adopted most probably because of the constant’s connection with the gamma function (extension of the factorial function). Despite being around for almost 300 years, gamma’s rationality is an open question. Also, it is unknown whether gamma is algebraic or transcendental.

How does the harmonic series relate to the logarithm function? That, precisely, is the content of this article. The process followed here relies on geometrical intuition, and is an archetype of a well established test for series convergence, the integral test.

Let

Then,

For better understandability, the article has been divided into four sections

• Proving that T_n (n in subscript) is bounded.
• Proving that T_n is monotonically decreasing, and hence, has a definite limit, ie, γ exists.
• Finding a tighter lower bound for γ.
• Some additional (rigorous) details around series convergence for interested readers.

T_n is Bounded

First, we give a lower bound to γ. Below is the plot for y = 1/x. Here, we exploit the well known trick of comparing the area under the plot with rectangular strips of unit width, with height being equal to the function’s value at that point.

From the above, it is clear that

Generalising, we get

Having proved that T_n is bounded from below, we now proceed to prove that it is bounded from above as well, via a slight manipulation of the above method.

Previously, the area of the rectangles dominated the area under the curve. What about the other way round?

Let’s see.

In this case

Again, generalising, we get

Combining above two results, we get

Therefore, T_n is bounded.

T_n is monotonically decreasing

Now we prove that T_n decreases monotonically, ie,

Proof —

Recall the Taylor series expansion for ln(x) —

Now

Therefore, we can safely use the above Taylor series expansion. Continuing —

Now, observe that,

Which means that the first term as well as each term in the summation above is negative. Thereby proving that

Hence T_n is monotonically decreasing.

Now, combining the two facts —

• T_n is bounded.
• T_n is monotonically decreasing.

and using the monotone convergence theorem, we get that T_n indeed converges to a fixed limit. That is, γ exists.

Providing a tighter lower bound for γ

On the basis of the above, we can confidently say that

But can we get tighter?

What if we used trapeziums in stead of rectangles?

Given the convex nature of y = 1/x, the trapeziums cover more area than the curve.

From the above, we see that —

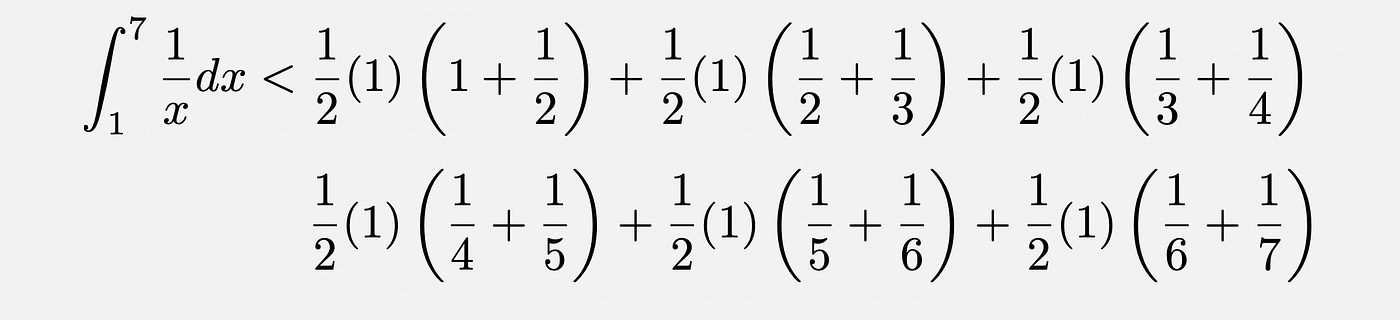
Again, generalising, we get —

Now, since

Therefore, we have —

Thus we have improved our lower bound for γ from 0 to 1/2.

As it turns out, the value of γ, correct upto 5 decimal places is 0.57721, not that far from our lower bound!

Additional stuff around sequence convergence

This is an auxiliary section, wherein we explicitly prove a result which we have already (implicitly) used in the above sections.

Let there be two sequences —

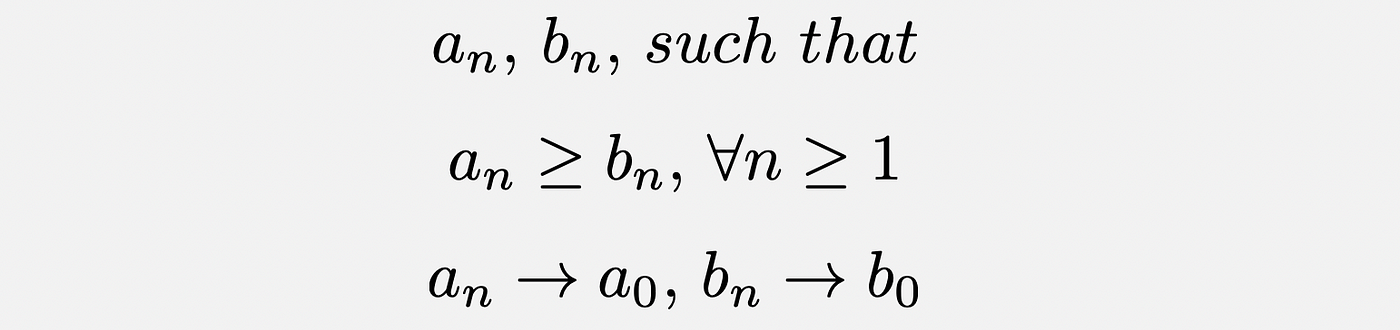
Then, we must have —

Proof —

Firstly, let’s recall what is meant by sequence convergence.

Now, we construct a proof by contradiction.

The last line above means that for n > N₀, a_n is restricted to r-neighbourhood of a₀ and b_n is restricted to r-neighbourhood of b₀.

To put it visually —

The above makes it obvious that —

Thus we have arrived at a contradiction. Hence our assumption (a₀ < b₀) is false. Therefore, a₀ ≥ b₀.

Thanks for reading through. Hope you enjoyed the article.

And, keep in mind, γ’s rationality and transcendence are still wide open questions up for grabs!