The Chaos of Weather Prediction

Since existence, humans have been trying to predict the weather. Early methods looked to astrology and the lunar phases. Even the Bible contains references to Jesus deciphering local weather patterns! And it makes sense, understanding the weather would offer immense advantages both in the battlefield and for agriculture.

However, like many achievements, it took a major conflict to really stir us into action. World War 1 really highlighted the need for accurate predictions of the weather. Both sides depended on knowing wind patterns for bombing raids and the drift of poison gas. This led to immense efforts to improve our understanding of these complex predictions. Attempts during this era were largely unsuccesful, as we just simply lacked the computational power. Forecasts would take days to run through and simply were not accurate enough. Instead, we relied on heuristic predictions that were far from reliable.

That all changed as computers slowly became more advanced. John von Neumann led the charge toward numerical forecasting. He envisioned future humans with the ability to completely control the weather due to both the accuracy of predictions and the ability for computers to know exactly what would happen given any pertubation.

Oh how wrong he was.

Edward Lorenz was freshly minted graduate in mathematics from Dartmouth in 1938 when he was called to war. There, he worked as a weather forecaster. Forecasting was still primitive, but was gradually being improved due the telegraph and the ever-growing amount of data available. This sparked an interest in meteorology, in which Lorenz received his doctorate from MIT, but he never really lost his mathematical mind.

Lorenz, along with Ellen Fetter, worked in the 60’s to develop a set of differential equations that could model the weather. For one of his studies, he examined a “cell” of atmospheric convection (think of this as air circulating) between a hot plate and a cold plate and watched how it changed over time. This model, seen below, had 3 different equations.

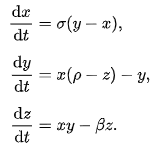
Lorenz’s first equation describes the convection itself. The variable x gives the rate of convection, and this equation describes how that rate evolves with time. His other two equations deal with temperature gradient, with y in the horizontal and z in the vertical. σ, ρ, and β are empircal variables that Lorenz varied to get different results. For more detailed explanation on working through the math, check out this fantastic piece. The Lorenz Equations show up in a slightly different form at the bottom of page 3.

This set of equations is deceptively complex and can quickly get out of hand. The symbol ρ is referred to as the Rayleigh Number, which gives insight into how heat is transferred due to convection. When ρ < 1, this system will eventually settle into an equilibrium with x, y, z all being 0. However, this is not what we observe in nature. Lorenz used the values σ = 10, ρ = 28, and β = 8/3 based on observation. See Figure 1 for an example of this system using these parameters and initial conditions (0, 1, 0).

If we plot z and x on the same axis, we get the famous Butterfly Plot as seen in Figure 2 below.

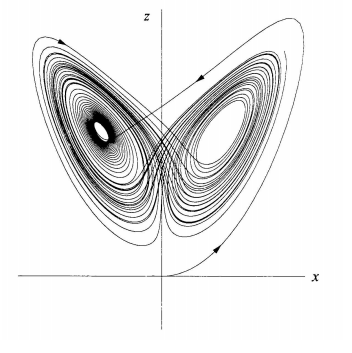
But what do these pretty pictures tell us about the weather? Scientist knew it would be complicated, but won’t we know exactly what will happen if we just get enough data? Like many things in science, a discovery was made completely on accident. Lorenz wanted to redo an earlier model run, but didn’t want to have to wait for the entire process (computers were slow back then). Instead, he input the x, y, and z values from halfway through and let it work from there. What he found shocked him. The solution began to move further and further away from his previous run, eventually becoming unrecognizable. Turns out, his input values were slightly less precise than the values that the computer was using. This very slight change in input drastically changed the output. You may know this as the Butterfly Effect.

This observation went against all previous intuition related to the weather. Yes, we knew it would be complex, but we had no idea how even the slightest imprecision would create massive inconsistencies. This also disproved John von Neumann’s idea about weather prediction; it was just too chaotic!

Modern weather forecasting only tries to limit the chaos; it is now accepted that it will never be able to eliminate it completely. This is done through ensemble forecasting, which was suggested in the 70’s and began being implemented in the 90’s. In this method, many simulations are done with varying initial conditions and the results are average to produce the most likely outcome. Newer versions will utilize different mathematical models as well and average those outcomes together.

Anyone who’s looked at the forecast know that we have a long way to go with weather prediction. Chaos Theory is still young field with so much to offer! For an informal introduction, I highly recommend Chaos by James Gleick. It does a lot to put the theory in historical context and gives you the basics. For more details and problems to work through The Nonlinear Workbook. This book is full of example and problems (some are coding based!) that help give an idea of just how varied the field is!

Thanks for reading! Leave a comment if you have any thoughts or questions about this article.