If your math teacher were to start a lesson from asking about your associations of the central angle theorem, would you answer by talking about the Thales theorem? If yes, what got back would be, “Yes, but only in one-third.” That is because an arc on which our inscribed angle could be subtended may have a semicircle, a major, or minor length. The semicircle one is known as the Thales theorem. And, we will start with its explanation at first; but just before beginning, for the comfort of reading, let us familiarize ourselves with definitions that are going to be used.

Vertex: a point where two lines (in our case) meet.
Diameter: Any straight line segment that passes through the center of a circle and whose endpoints lay on the circle. There is an infinite amount of possibilities to draw it.
Chord: the straight line segment connecting any two points on a circle, where the diameter is the longest one.
Arc: part of the circumference of a circle.
Central angle: the angle at the center of a circle between two radii.
Inscribed angle: the angle of a vertex on a circle between its chords. 
An angle subtended by the arc: A vertex whose chords’ endpoints enclosed the given arc.

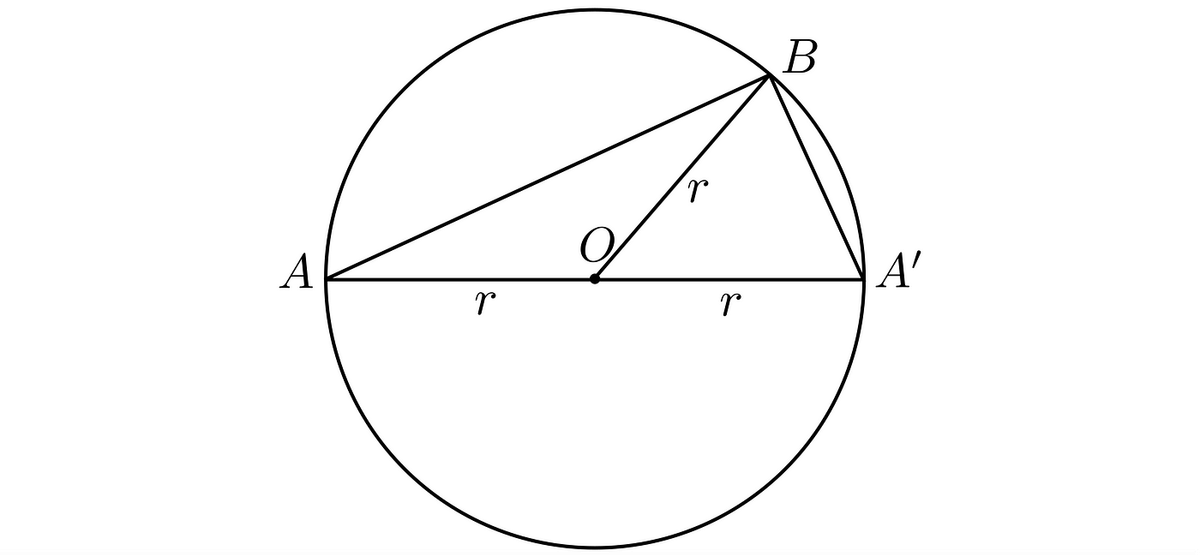
The Thales theorem, semicircle arc, central angle 180°

When a diameter goes through the center of a circle, then the central angle subtended by the semicircle arc is simply 180°, no doubt about that. And, if the theory is right, any inscribed angle whose chords’ endpoints are at the corresponding endpoints of this diameter should be twice less — it should be 90°. So we would have a right triangle, where the diameter is the hypotenuse.

Let us denote the diameter endpoints as A and A’, their angles as α and α’, and vertex of this inscribed angle, ß, as B. By connecting them, we got a triangle. Moreover, it would be the right triangle since the inscribed angle is right angle; with the diameter being its hypotenuse.

It looks like this:

Ready? Steady? Go! To prove this extremely useful theorem.

The geometrical proof for convenience

Notice that segments from the center O of the circle to the vertices are its radii. And they divide the AA’B triangle in the two other, but not any triangles. They have to be the isosceles ones because each has two equal sides that are equal to the radius of our circle.

Yet, both angles between the radii sides and the 3rd leg have to be equal; therefore, ß=α+α’.

And we know that the sum of angles in a triangle is 180°. By adding all them of AA’B triangle, we get:

So, indeed ß is right angle.

q.e.d

The Pythagorean proof for a little fun

Initially, I titled this section as “The Pythagorean proof”, but I enjoyed writing it so much that the extra “for a little fun” had to be denoted here.

We assume that the inscribed angle ∠ABA’, being twice less than the central one, is right. If that is the case, then the Pythagorean theorem must hold.

Do not bother yourself about the θ angle; it will be explained just in a second, but first, let us applied the formula to show what we are trying to prove, that is:

This θ is simply the angle about which a line is tilted from the origin. That is all.

Having it, we could decompose our line into components along the axis. And with a little help from the trigonometry, we could compute them: components written in such a way are known as the polar coordinates.

Let us back to the proof itself. We need to decompose the sides along right angle into x, y-components, and then by applying Pythagoras’ theorem compound both their length.

The length of AB:

Note that the x-component is the addition of r and r ⋅ cosθ. While the y is composed of a single value.

The length of A’B:

What is worth to mention here is the x-component length, unlike the same one earlier, force us to subtract from r the r ⋅ cosθ. Also, see and compare the y-components: they are equal. What, if think about this, should not be a surprise.

Now, we could get back to our initial formula, substitute these values, and check whether its sides are equal or not.

As seen, everything is correct — and better be.

q.e.d

Major arc (>180°)

What distinguishes the major (and minor) case from the Thales one, is the fact, that now, radii does not form a diameter. Those radii create a larger central angle than 180°. It means that, if the theorem still holds, any inscribed angle being twice less is larger than 90°.

It looks like this:

The geometrical proof

Three things are needed to prove this (and the next) case. Two of them are already known to us: The segments from the center of a circle to each vertex are radii. And they divide our figure into two isosceles triangles. But what is the third?

If we “copy” the OB, and turn it around the perpendicular axis noting the opposite point on the circle as B’, we would get a diameter.

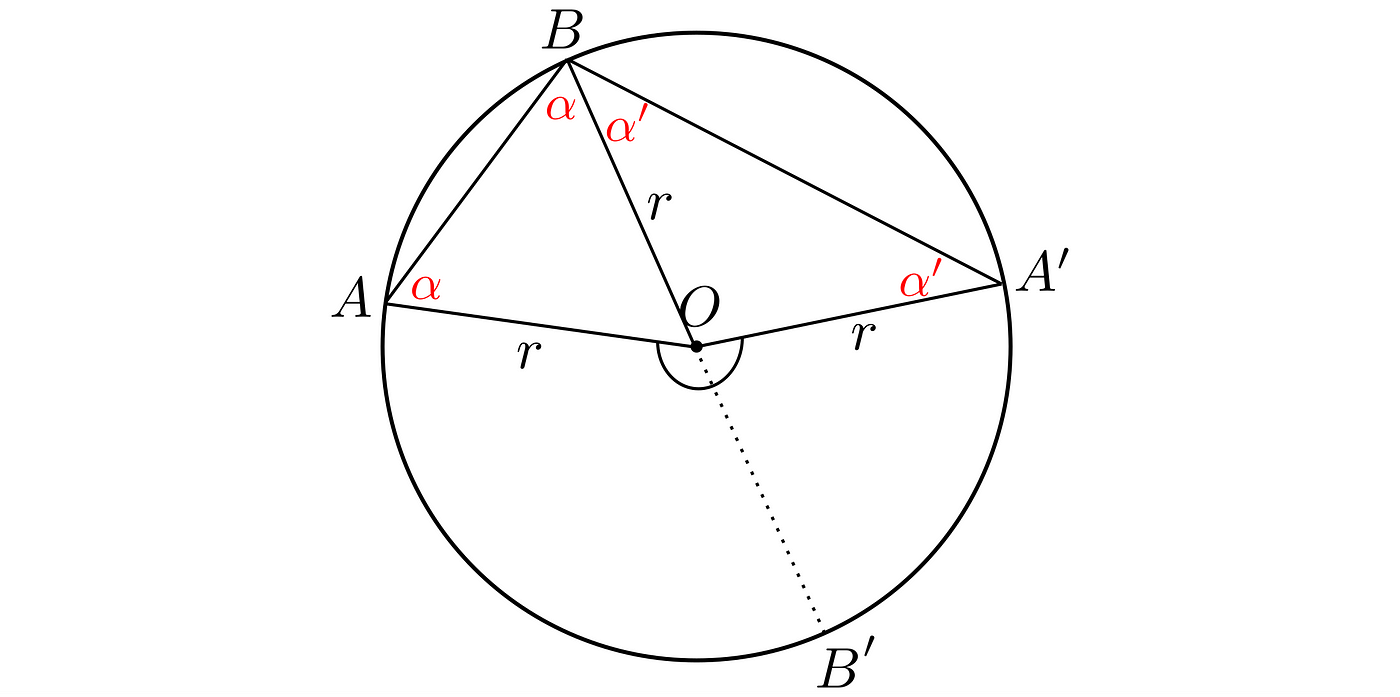
Now, by drawing one extra chord from B’ to each A and A’, we could separate this whole problem into two, say, a left and a right. Where both could be examined by the Thales theorem because BB’ is the diameter, the central angle is 180°, and the inscribed angle ∠BAB’ and ∠BA’B’ are 90°. Of course, ABB’, A’BB’ are right triangles.

The left one looks like this:

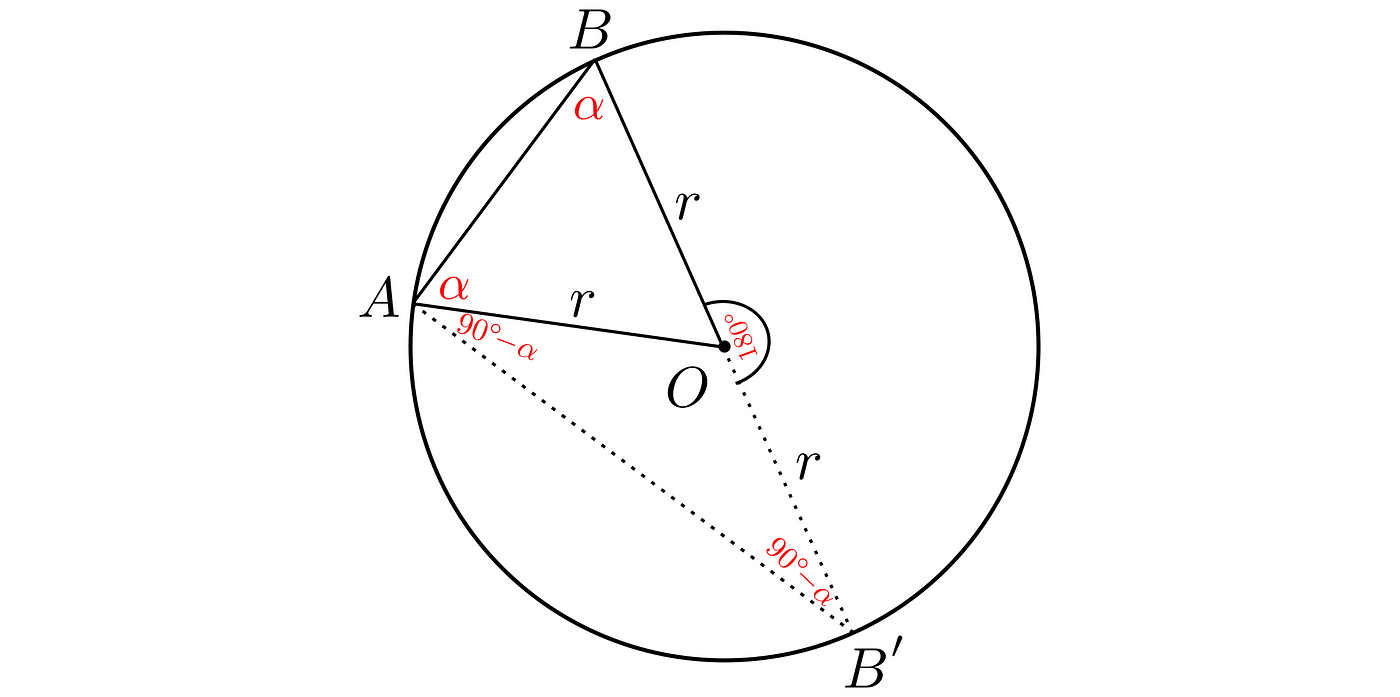
By finding the ∠AOB’ angle, we will know what the left part of the central angle is. What it could be? The angle ∠BAB’ is 90°, but since its upper part is α, the lower one has to be 90°-α, and the angle ∠AB’O has to be the same! So, by summing angles in the lower triangle, we get:

Thus the left part of the central angle is indeed twice as much as the α.

The decomposed right part looks like this:

And we do everything in the same way as with the left part, getting:

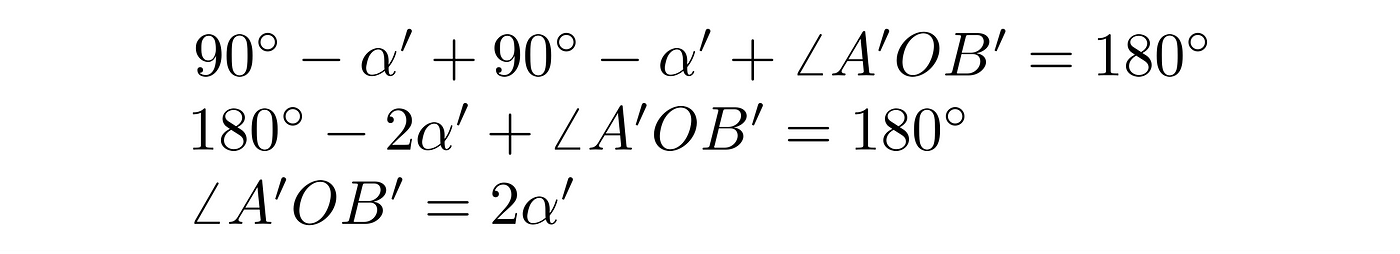
Hence, indeed, the central angle is twice as any inscribed one subtended by the same arc.

q.e.d

Minor arc (<180°)

The last case, when the central angle is less than 180°. All steps are identical to the major case. But first, let us take a look at what it looks like:

The geometrical proof

What we do is providing the BB’ diameter that will again slice our problem into a left and a right.

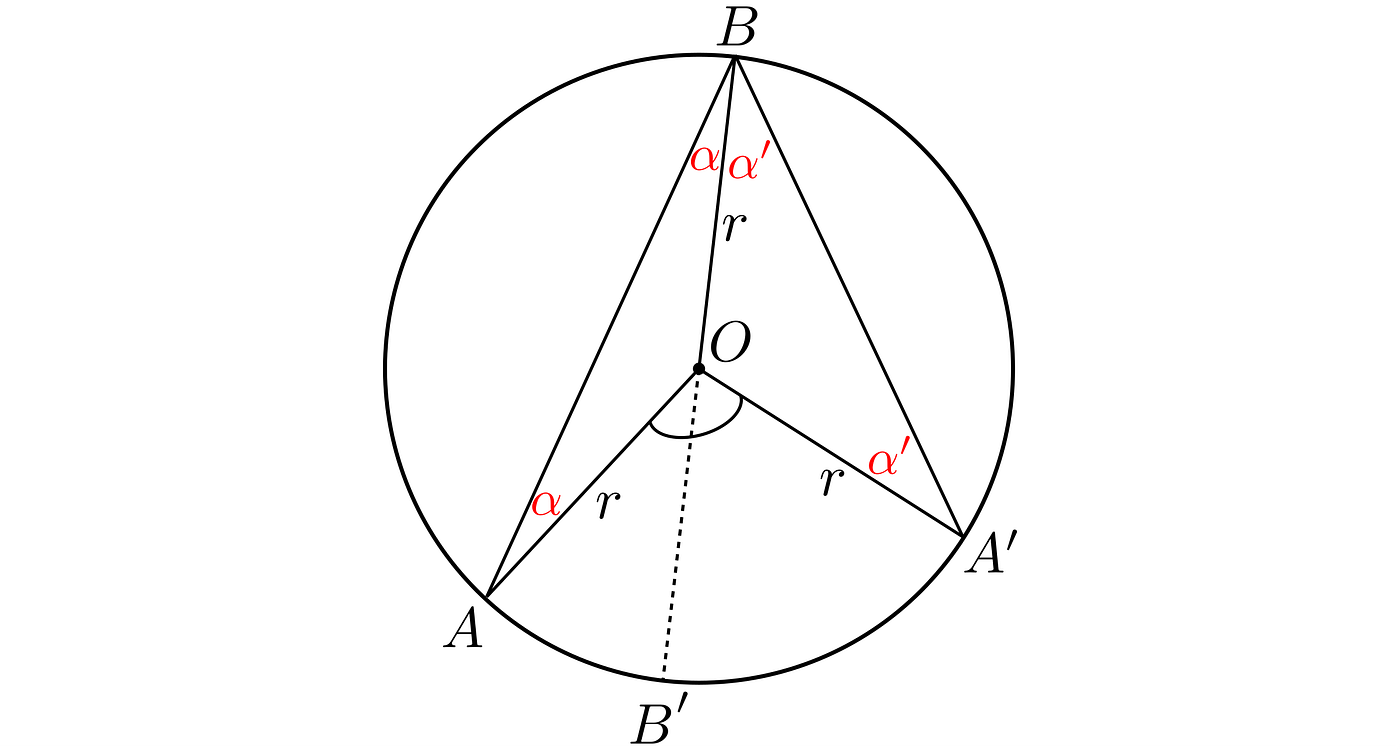
The left one:

The angle ∠BAB’ is 90°, and its upper part is α. Thus the lower part has to be 90°-α. The angle ∠AB’O has to be exactly the same. Thus, the sum of the angles in the lower triangle are:

After applying the situation is as follows:

The right one:

And for the last time, the inscribed angle ∠BA’B’ is 90°. Since its upper part is α’, the lower one has to be equal to 90°-α’. Also, the angle ∠A’B’O is the same in size. By summing the angles in the lower triangle we get:

which gives:

So, in this case, the central angle theorem works as well.

q.e.d