Ever wondered what happens to a raindrop during its journey from clouds to the ground? It does not stay intact. It deforms and breaks as it comes down. According to Villermaux and Bossa, the raindrop flattens as it comes down and forms a bag-like structure before it breaks (I strongly recommend watching the supplementary movie on this page for the high-definition video).

Why does a Liquid Droplet Break?

A liquid droplet assumes a spherical shape because of surface tension. The force of surface tension tries to minimize the surface area of a liquid droplet for a given volume. Since a sphere has a minimum surface area (Sₘᵢₙ) for a given volume, the droplet takes a spherical shape. The force of surface tension opposes any shape change from a sphere as the new shape has a surface area greater than Sₘᵢₙ. Hence, to break a droplet into smaller droplets, which involves increasing the surface area, a force greater than the surface tension of the liquid is needed. Where does this force come from? In the case of a falling raindrop, this force arises because of the relative motion between the falling raindrop and the surrounding air. This force can be called as an aerodynamic force. The basic requirement for creating the aerodynamic force for breaking a liquid droplet is the presence of relative motion between the droplet and surrounding gas flow-field. The magnitude of this aerodynamic force depends on the magnitude of the relative velocity between the droplet and the surrounding gas flow-field. For example, the magnitude of the aerodynamic force in the case of a falling raindrop in a quiescent surrounding (air is stationary) is lesser than in the case of the falling raindrop in an ascending stream of air, because the magnitude of the relative velocity is larger in the latter case, and thus the potential for droplet breakup is more in the latter case. But how large should this aerodynamic force be in comparison to the surface tension force to induce droplet breakup? In other words, what should be the minimum value of the ratio of this disrupting aerodynamic force to the surface tension force to induce droplet breakup? This ratio of the disrupting aerodynamic force to the surface tension force is known as the Weber number (We). Experimentally, it was found that the minimum value of the Weber number needed for droplet breakup to happen is We = 11±2. It is not as though the droplet breakup does not happen for We < 11. But, this breakup is not practically useful (it is discussed later). Also, for We < 11, the droplet breakup is not always guaranteed. However, for We > 11, the droplet breakup is always guaranteed. And, this breakup is practically useful too. So, let’s look at how a liquid droplet breaks for We < 11 and We > 11?

How Does a Liquid Droplet Break?

(a) For We < 11

For We < 11, the disrupting aerodynamic force is not strong enough to overcome the surface tension force completely. This makes the droplet oscillate, and sometimes break. This breakup is known as vibrational breakup. In this breakup, the droplet breaks into 2 or 3 droplets whose sizes are comparable to the parent droplet.

But why does a droplet oscillate before it breaks? As long as We > 1, the disrupting aerodynamic force is greater than the surface tension force. Then, instead of breaking/disintegrating, why should a droplet oscillate?

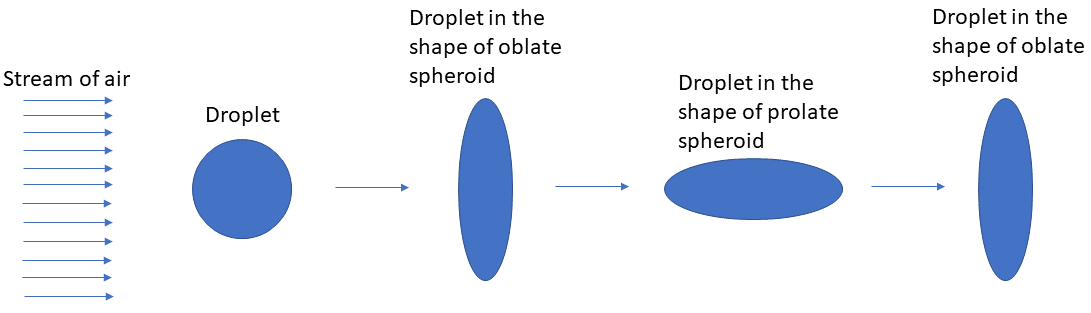
Figure 1 shows a droplet in a stream of air for which 1< We < 11. It was observed experimentally that the droplet takes shapes of oblate and prolate spheroidsduring its oscillation (Fig. 1). Let’s look at the mechanism which makes the droplet oscillate.

The relationship between the pressure inside and outside the droplet is represented using the Laplace law:

where pᵢₙ and pₒᵤₜ represent the pressures inside and outside the droplet, σ represents the surface tension of the liquid, κ represents the droplet surface curvature (the local bending of a curve or a surface), and R₁ and R₂ represent the principal radii of curvature. The ‘principal directions’ associated with R₁ and R₂ are perpendicular to one another. For a point on a surface, the principal radii of curvature are the radii of the osculating circles to the resulting curves formed by sectioning the surface by principal planes of curvature at the point of interest, and the principal planes of curvatures are also perpendicular to the surface tangent plane at the point of interest. OKAY, THAT’S TOO MUCH!! Let’s break it down.

As mentioned before, the droplet attains three different shapes during its oscillation for 1 < We < 11: a sphere, an oblate spheroid, and a prolate spheroid (Fig. 1). Let’s find out the expression for curvature κ for each of these shapes.

Figure 2 shows a spherical droplet. Consider point A on the droplet surface. A surface normal Aₙ and a surface tangent plane Aₚ, both at point A, are shown. Now, we want to measure curvature κ at point A. To calculate that, we need the principal radii of curvature which are perpendicular to each other and also lie in the principal planes of curvature. The principal planes of curvatures, represented by B and C in Fig. 1, are perpendicular to the surface tangent plane A, and also perpendicular to each other. The intersection of these principal planes with the local surface around point A form 2-D curves: curve Cc is formed by the intersection of plane C with the local surface, whereas curve Cb is formed by the intersection of plane B with the local surface. Figure 2 also shows the osculating circles of the curves Cc and Cb. Their radii Rc and Rb are the principal radii of curvature.

Since it is a sphere, the osculating circles have radii equal to the radius of the sphere (Rc = Rb = R). Hence, for a spherical droplet, equation (1) implies,

For any point on the spherical droplet, the above analysis results in the same expression for the pressure difference (pᵢₙ −pₒᵤₜ) across the interface of the droplet. Let’s do a similar analysis for a droplet having the shape of an oblate spheroid.

An oblate spheroid has different curvatures at different points on its surface. Figure 3 shows a droplet having the shape of an oblate spheroid. Here, we do a similar analysis, as we did in the case of the spherical droplet, for two points: U (one of the poles of the droplet as seen in Fig. 3a) and X (a point on the equator of the droplet as seen in Fig. 3b). Terminologies used here are similar to the ones used in the case of the spherical droplet.

For point U (Fig. 3a), equation (1) implies,

Similarly, for point X (Fig. 3b), equation (1) implies,

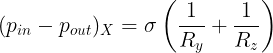
Now,

But, pₒᵤₜ is the same for both the points U and X (this is true for slow-moving droplets). Hence,

The inside pressure at U is less than the inside pressure at X. It means that there is a resistance to liquid flow from U to X, i.e., from poles to the equator. Hence, surface tension and the droplet curvature act such that they resist a shape change from a sphere to an oblate spheroid.

Let’s do a similar analysis for a droplet in the shape of a prolate spheroid. Figure 4 shows a droplet having the shape of a prolate spheroid.

For point I (Fig. 4a), equation (1) implies,

Similarly, for point P (Fig. 4b),

Now,

Again, pₒᵤₜ is the same for both the points I and P (this is true for slow-moving droplets). Hence,

There is resistance to the liquid flow from point P to I, i.e., from equator to the pole. Hence, the droplet in the shape of an oblate or a prolate spheroid always has a resistive force which tries to bring back the shape to a sphere. The higher the curvature of the droplet, the higher is the resistive force.

During droplet oscillations, as the force of surface tension brings back the droplet from oblate spheroid to a sphere, it overshoots the equilibrium shape (i.e., sphere) and forms a prolate spheroid. A similar thing happens when the droplet changes shape from prolate spheroid to oblate spheroid. These oscillations sometimes become unstable which leads to droplet breakup into 2 or 3 droplets whose sizes are comparable to the parent droplet size. However, for practical purposes, this type of breakup is not desired as there is not a significant increase in surface area of the droplet after the breakup, which is the primary purpose of a droplet breakup/atomization process in practical applications.

The oscillating droplet can be considered as an oscillating mass-spring system. The external force on the spring is analogous to the disrupting aerodynamic force on the droplet, whereas the restoring force of the spring is analogous to the surface tension force of the droplet (a droplet breakup model known as the Taylor Analogy Breakup model, which is used in spray simulations, is actually based on this analogy).

Till now, I have not considered the effect of viscosity on the droplet breakup. Viscosity also resists droplet deformation. However, for many practical cases, the effect of viscosity is negligibly small. Hence, I have not discussed its effect here.

(b) For We > 11

As the Weber number increases beyond 11, the aerodynamic force becomes strong enough that the surface tension force cannot bring back the droplet to its spherical shape and make it oscillate. The droplet deforms into a shape like an oblate spheroid, and then, it forms different structures depending on the mode of breakup before disintegrating into a multitude of smaller droplets. This mode of breakup depends on the value of Weber number. As the Weber number increases from 11, the mode of breakup changes from bag breakup, bag-stamen breakup, shear breakup to catastrophic breakup. These breakup modes occur in different ranges of Weber numbers, e.g., the bag breakup occurs in 11 < We < 16, and the bag-stamen breakup occurs in 17 < We < 30. Figure 5 shows grayscale images of different breakup modes (these images are taken from this report). The times are shown in milliseconds. The droplet breakup happens on short time scales. Hence, to study it, high-speed cameras are used.

For We > 11, the droplet breakup is always guaranteed. Also, the sizes of product droplets formed after breakup for We > 11 are significantly smaller than those for We < 11. Since the primary purpose of a droplet breakup/atomization process in a practical application is to increase the surface area of the liquid by disintegrating it into smaller droplets, droplet breakup for We > 11 has received serious attention from several researchers. The droplet can break via any of the breakup modes mentioned above depending on the value of the Weber number. The breakup modes differ in characteristics such as the morphology of breakup, droplet size distribution of the product droplets, breakup times, etc. The physical mechanism behind each of the breakup modes is still under debate. However, numerous experimental and numerical works have revealed valuable information regarding these breakup modes. Such information is useful for designing and developing spray nozzles, injectors, atomizers in practical applications.

References

1. M A Rodrıguez-Valverde, M A Cabrerizo-Vılchez, and R Hidalgo-Alvarez, The Young–Laplace equation links capillarity with geometrical optics, EUROPEAN JOURNAL OF PHYSICS, 2003.
2. J. Tan, M. Papadakis, and M. K. Sampath, Computational Study of Large Droplet Breakup in the Vicinity of an Airfoil, Technical report, 2005.
3. Emmanuel Villermaux and Benjamin Bossa, Single-drop fragmentation determines size distribution of raindrops, Nature Physics, 2009.
4. Myth of raindrop formation exploded (https://www.newscientist.com/article/dn17487-myth-of-raindrop-formation-exploded/)
5. Weisstein, Eric W., Osculating Circle, From MathWorld — A Wolfram Web Resource (https://mathworld.wolfram.com/OsculatingCircle.html)
6. Spheroid (Wikipedia)