Solving the Basel problem, using an elementary introduction to Fourier series!

Part 0: Motivation, some History, and Welcome!

Hello and welcome!

We are going to be tackling a beautiful problem, the ‘Basel Problem’. It was posed in 1650 by Pietro Mengoli, and it took 84 years to solve it, when the brilliant Euler did so.

Euler’s proof was brilliant, but also not strictly speaking complete! He used manipulations which couldn’t be justified with the mathematics developed at that time. It would take 100 years before the gaps in Euler’s proof were completely filled. It was the brilliant analyst Karl Weierstrass who developed the underlying theories that would eventually validate Euler’s argument.

We will follow a different path.

In our approach to the problem, we learn the basics of fourier series. Fourier series, pioneered by Joseph Fourier to solve the heat equation, decompose functions into trigonometric components, and their generalisations remain active areas of mathematical research.

It turns out that we can generalise some of our intuitions about 2 and 3-dimensional space when talking about functions! We explore why this is true, and then use our new tricks to crack open the problem. This won’t be easy (otherwise it wouldn’t have taken over 80 years to solve!), but will be very rewarding.

Good luck, and enjoy :)

Part I: the geometry of functions

We are all familiar with geometry. The gameplan is to extend our intuitive notions of geometry to a new mathematical setting.

First we consider 2 dimensional space. A point in two dimensional space is a very simple object. Importantly, we can ‘decompose’ the point into its x-component and its y-component, as done by the dotted lines below

We can do the same in three dimensions! We take a point, and intuitively we can express it as a certain height, a certain width and a certain length. In two dimensions we say we have an ‘x-axis’ and a ‘y-axis’. In three dimensions we have an ‘x-axis’, ‘y-axis’ and a ‘z-axis’.

Crucially, in both cases, the axes are ‘perpendicular’, or at right angles to each other. The idea of arrows, or axes, being perpendicular is actually quite a broad notion. Let’s understand why:

Given some mathematical objects, such points in 2-dimensional space, it is helpful to be able to express these objects as sums of simpler objects. In the case of two dimensional space, by breaking down a point as an x-component and a y-component, it becomes easier to visualise, to plot, and also to ‘add’ points together.

So, a more general idea might be the following: given some mathematical objects, find a subset of them from which we can build the others. We call this a basis. We then also want these objects to ‘point in different directions’ in a way similar to our perpendicularity of the x-axis and y-axis. To analyse more complicated objects, then, it is often sufficient to consider the simpler ones they are constructed from.

Trigonometric functions: sin(x) and cos(x)

The protagonists of your adventure will be some very humble functions: sin(x) and cos(x), which, miraculously, will be able to express very different functions through some ingenious mathematics.

As these two will be so important in our story, we remind ourselves of what they are here.

Given an angle, which we call θ, we get a position on a circle of radius 1. That position can be expressed as its x-direction and its y-direction. The x-direction is cos(θ), and the y direction is sin(θ).

One thing to note is that while normally people measure an angle θ in terms of degrees, which ranges from 0 to 360, in math we normally use radians. Then, we say there are 2π radians in a circle. This is done because it makes lots of formula’s and graphs a lot prettier and simpler to use. If you find this a bit confusing, it is just like how some countries use metric measurements (kilometres, kilograms, etc) while others use different measurements (miles, ounces etc), but both measure the same thing.

Another thing to note, is that while defining sin() and cos() in terms of angles, we normally use θ, in other contexts we call the input to the function x, which is somewhat confusing, as x is also the name given the the x-axis.

Perpendicular functions

Recall that a function takes in numbers and returns a number. It’s often helpful to visualise it with a graph

The graph below is for sin(x). Note that it repeats itself after 2π. That’s because, you might recall, there are 2π radians in a circle, so by 2π we are at the same point as when the angle was 0.

Now, let’s suppose we have a function which repeats itself in a regular way, and looks ‘moderately’ smooth. If it looks like you can draw a function by hand, then it is reasonable to assume it is ‘smooth’ enough for what we will do later.

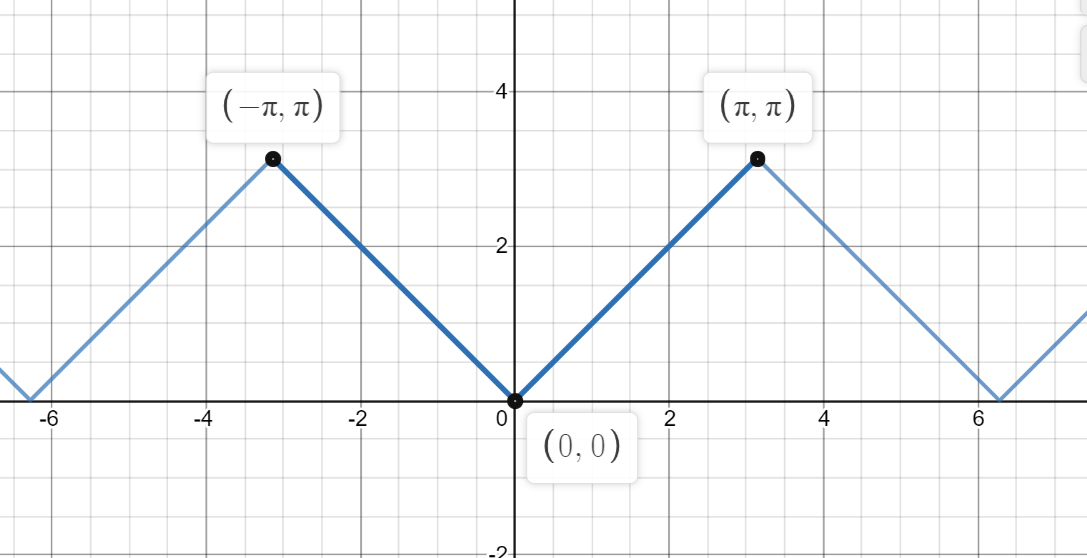
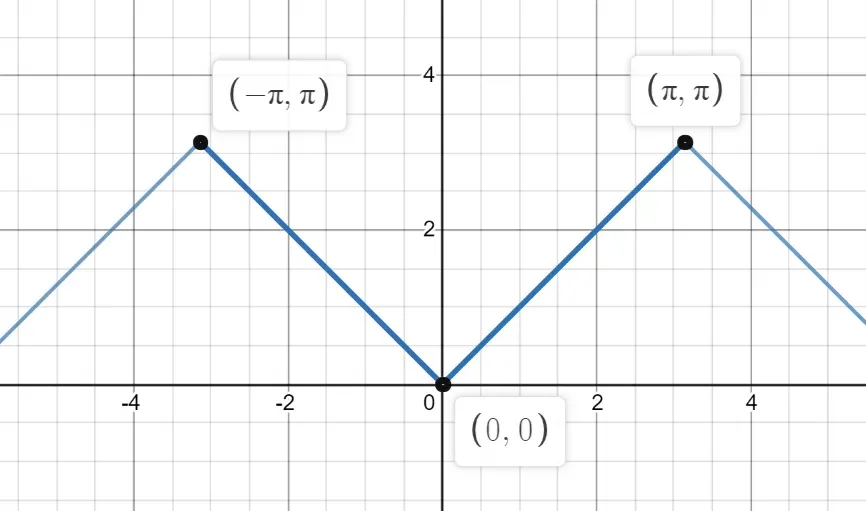
The function above looks like a repeating triangle with width 2π, and height pi. For -π≤x≤π, this function returns the absolute value of x. It is also clearly ‘periodic’, as the graph repeats.

Now, we are going to claim that for functions which are ‘periodic’ and ‘smooth enough’, like our function above, we can represent them as the (infinite) sum of trigonometric functions. Underlying this is that trigonometric functions are ‘perpendicular’ in a cleverly defined way. This is a miracle! sin(x) and cos(x) are functions which were invented to understand circles better, yet have this extraordinary versatility. (It turns out there are other functions which can be used like this, and have great use in mathematical physics and partial differential equations)

A Word of Warning

While many nice properties of our familiar two and three dimensional spaces carry over to our new ‘function spaces’, many things will not carry over. In particular, in two dimensional space, we can use just two(!) perpendicular directions to express any point (the ‘x’ direction and ‘y’ direction), whereas in a function space it turns out we will have a countably infinite number of perpendicular directions!! This makes things harder, but also waaaay cooler.

(A small aside on ‘smoothness’ conditions for the curious.)

This section is completely optional. Skipping it won’t effect your ability to understand the remaining math.

Why are mathematicians interested in these strange conditions like being smooth, or more precisely whether a function is ‘continuous’, ‘differentiable’, of ‘bounded variation’, ‘infinitely differentiable’, and so on?

It turns out that mathematics is really hard. But there are some properties which are not so difficult to check, and allow a lot of things to be proven in general. This is why university mathematics is quite intimidating (all the definitions and theorems), but underlying this is that we make mathematics easier by identifying the most relevant properties of the mathematical objects we study.

In the case of fourier series, the relevant conditions are known as the ‘Dirichlet conditions’, but there are also other conditions for the rate of convergence and other important properties.

Perpendicular functions continued. (Harder)

The following section will be a little tricky! If you get too stuck, moving along to the next section is ok, where we will have a more hands on application of the theory to begin solving the Basel problem. However, do give it a go, as good ideas take time to sink in :)

We define the following trigonometric functions:

sin(x), sin(2x), sin(3x), sin(4x), …

cos(x), cos(2x), cos(3x), cos(4x), …

We also need to define what it means for two functions, f(x), and g(x), to be perpendicular on the interval (-π,π). We do this using integrals!

In this new case of functions defined for inputs of x between -π and π, we are then saying f and g are perpendicular if the integral of them multiplied is 0.

Now, let’s see if the sin(nx) and cos(mx) functions are perpendicular. To do this we need the following formula:

We start with cos(x) and sin(x). If you aren’t too familiar with calculus, you can skip over this.

So, we have that:

Or in other words, cos(x) and sin(x) are ‘perpendicular’! The key idea here is that we are giving a ‘geometric’ interpretation to integrating the product of two functions, which will allow us to decompose functions similarly to how we decompose vectors in two or three dimensional space.

A lot of algebra later, we get the following key results:

• Case 1. For any integers ’n’ and ‘m’, sin(nx) is perpendicular to cos(mx). This is true even when n=m. We saw the case n=m=1 above. Example: sin(3x) is perpendicular to cos(2x) (n=3, m=2)
• Case 2. For any integers ‘n’ and ‘m’ which are not the same, sin(nx) is perpendicular to sin(mx). Likewise cos(nx) is perpendicular to sin(mx). Note that when n=m this is not true. Example: sin(5x) is perpendicular to sin(6x) (n=5, m=6).
• Case 3. For ‘n’= ‘m’, we have that sin(nx) is not perpendicular to sin(nx). This is very important, just as how the x-axis isn’t perpendicular to itself! Example: sin(11x) is not perpendicular to sin(11x).

In notation, we summarise these results as:

Once we have confirmed that our functions are ‘orthogonal’, we have the following expression for our function f(x):

Where:

i.e. c averages f(x) over the interval

And:

i.e. b_n gives the part of f(x) in the direction of cos(nπx)

And:

i.e. a_n gives the part of f(x) in the direction of sin(nπx)

We now press on and use this theory for some fun!! At the end of the article, I give a few more details on how to derive the above equations, for those who are really keen.

Let’s have some fun!

Now we have established some facts about when sin(nπx) and cos(mπx) are perpendicular, we treat these functions like we did the x and y coordinates of 2-dimensional space: we express a function f(x) as a sum of them!

Let’s remind ourselves what our triangle-like function looked like. It turns out for this function, we will only need the cos(x), cos(2x),…, cos(nx),… functions to represent it. *If you want to see the reasoning why we only need the ‘cos’ functions, the appendix goes into greater detail*

The first approximation we use is:

Visually this approximation is:

That’s pretty good. What if we throw in another term?

Wow!!! That is really good. Now we include over 10 terms of function’s fourier series.

Ok, we’ve had some fun :))

But let’s just do one more, using the first 100 terms!!

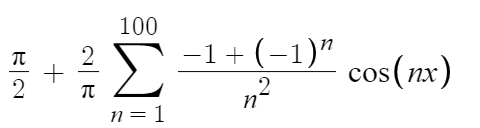
So, fourier series are awesome. I think you’ll now believe me if I said if we include all infinite terms of the approximation then the approximation becomes perfect!

We now use this to solve the Basel Problem!!

Part II: solving the Basel Problem

We use all our terms of our approximation to the ‘triangle’ function.

Now we do something astonishingly simple. We simply approximate our ‘triangle’ function as x=0.

Note for enthusiasts. Many hard problems in mathematics are actually applications of more general principles, but the specifics of the problem makes it difficult to see that we should apply the more general principle. This is the case here.

Observe that cos(0) = 1. Plugging in our approximation at x = 0, we get:

We now write this explicitly, and rearrange:

We are nearly done!! (The ‘dots’ ‘….’ after a sum indicate that it is an infinite sum)

We make a simple observation. (If you don’t see why it is true at first, write out the first few terms by yourself to see why the equality holds)

The aim is to use this observation to tie the sum of the basel problem to the identity we deduced above:

The above step simply states that the sum of the reciprocals of the odd squares is the sum of the reciprocals of all squares minus the reciprocals of the even squares. We combine this with the first observation:

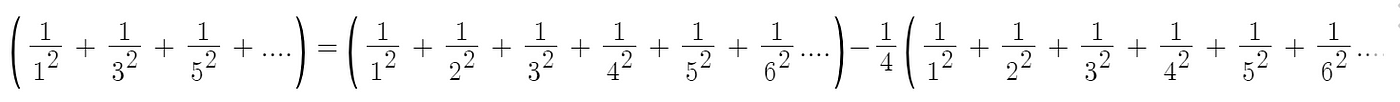
We are now within striking distance of the Basel problem!!

After all, we have already calculated the term on the left hand side!!

To finish the job, we re-arrange,

Q.E.D. □

Thank you to Bartek Pierzchała, for advice and proof reading, and more generally for being a cool dude, and making me laugh during lockdown.

I am a mathematics student at cambridge university, UK. Thank you for taking the time to learn some new math!! I will try to reply to all comments left below :)

Appendix: more details on the fourier series derivation. (Harder, and optional)

Some of the theory for fourier series’ existence and convergence is quite subtle. Here we don’t go into all the technical detail, but do explain a little more how to derive some of the formulas.

Let’s look at a worked example.

In general, we have the expression:

Let’s see if we can use the ‘orthogonality’ of our functions. What happens if we integrate the following?

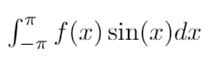
Let’s press ahead, plugging in the series expression for f(x)

We expand this expression:

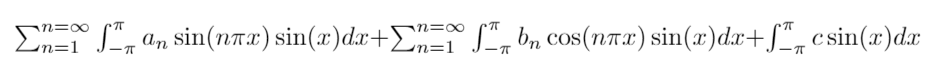
Aha! But now we can use our orthogonality conditions. This is because sin(x) is orthogonal to all the functions in the expression above except itself!! This allows the fantastic simplification to:

Hence, we get:

We already have an expression for the integral of sin²(x) from -π to π

Bringing this all together yields:

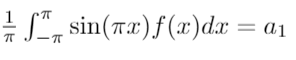
A very similar argument holds for all the other coefficients.

This also sheds light on what may have been a confusing step in the fourier series of the ‘triangle function’ we used earlier. I stated that we only needed cos(x), cos(2x), cos(3x), … cos(nx),… to represent it, and didn’t need sin(x), sin(2x) … and so on. The reason for this can now be better understood.

You may have noticed that our triangle function is an even function. This means that f(x)=f(-x). In simpler language, it is symmetric in the y-axis.

If we zoom in a bit, this is visually obvious

Now we look at f(x)sin(x):

We see this function is odd: the values to the left of the origin are simply -1 times those on the right hand side. Importantly for our purposes, when integrating, which gives us the area under the curve, the areas to the left and the right of the origin cancel.

The same principle can be seen when we multiply our function by sin(3x)

With a little work, we see that for our triangle function, all the coefficients of the ‘sin(nx)’ terms are zero, i.e. that

and therefore we can write it purely in terms of ‘cos’ terms.

P.S. if you made it to the end (well done!!), and have thoughts on how I could improve the article, I’d love to hear them below :)