Grothendieck

The Anarchist Abstractionist — Who was Alexander Grothendieck?

Mathematician Alexander Grothendieck was born in 1928 to anarchist parents who left him to spend the majority of his formative years with foster parents.

Jørgen Veisdal

Jørgen Veisdal

— 27 min read
The Anarchist Abstractionist — Who was Alexander Grothendieck?
Alexander Grothendieck in 1951, 1965 and 2014 (Photos by Paulo Ribenboim, Karin Tate and Peter Badge)

“The greatest mathematician of the 20th century” — Le Monde

Mathematician Alexander Grothendieck was born in 1928 to anarchist parents who left him to spend the majority of his formative years with foster parents. His father was murdered in Auschwitz. As his mother was detained, he grew up stateless, hiding from the Gestapo in occupied France. All the while, he taught himself mathematics from books and before his twentieth birthday had re-discovered for himself a proof of the Lebesgue measure, a staple of integration theory. Later a rising star in the hot-shot French mathematical milieu of 1950s and 60s, Grothendieck would in his “golden years” from 1955–1970 move from subject to subject, introducing revolutionary new ideas as he went along:

“This just kept happening over and over again, where he would come upon some problem that people had thought about for, in some cases, a hundred years […] and just completely transformed what people thought the subject was about” — Nick Katz, Princeton University

In 1966 he was awarded the Field’s Medal, mathematics’ highest honour for his contributions to algebraic geometry, homological algebra, and K-theory. Four years later, he famously abandoned his professorship at the “French Institute for Advanced Study” for political reasons. Indeed, he left mathematics altogether in 1991 to instead live in seclusion in a remote village at the foot of the Pyrenees Mountains. Rarely ever seen or heard from since, he spent the last twenty-three years of his life in isolation, refusing to communicate with anyone, at times attempting to sustain himself on “a diet of dandelion soup” while writing thousands upon thousands of pages of text on spirituality and a “coming day of reckoning”.

This week’s newsletter is about Alexander Grothendieck, perhaps the most technically gifted mathematician of the twentieth century. Feel free to share newsletter with anyone who might be interested:

Share

Early Life (1928–42)

Left: Young Alexander Grothendieck. Right: Alexander with his foster-parent Dagmar Heydorn in Hamburg during the 1930s (Photos: unknown)

Alexander Grothendieck was born in Berlin in 1928 to anarchist parents Alexander “Sascha” Schapiro and Johanna “Hanka” Grothendieck. His father was Russian and of Jewish ancestry, having been born in what is now Ukranine and growing up in the Russian Empire. Sascha fought in the Russian Civil War opposite the Red Army, where he lost an arm during an escape from a prison, a crime for which he was sentenced to death before being pardoned due to his young age. Following a suicide attempt, he was in 1914 placed in involuntary solitary confinement for a year. Born to a wealthy family, his father in 1922 moved to Berlin where he met Alexander’s mother, journalist and writer Hanka Grothendieck. Their son was given the surname of his mother, who stemmed from a well-established middle-class family in Hamburg. The name Grothendieck is Plattdeutsch, a Northern German dialect (Pragacz, 2004).

Alexander “Sascha” Schapiro (1889-1942) and Johanna “Hanka” Grothendieck (1900-1957) (Photos: unknown)

Alexander lived with his parents for the first five years of his life until the end of 1933, when the the “great purge” of Jewish intellectuals, academics and political figures forced his father to flee to France. His mother joined him there soon after, leaving their five-year old son in the care of a Lutheran pastor and teacher by the names of Wilhelm and Dagmar Heydorn. Starting in 1936, Alexander’s father Sasha fought in the Spanish Civil War in the resistance alongside other anarchists in opposition to the Franco regime.

Class photograph from Le Collège-Lycée Cévenol International in the early 1940s. Grothendieck is standing, third from the right, barefoot (Photo: unknown)

Alexander continued living in Hamburg until 1939 when it was decided that the young Grothendieck should seek refuge too, and so he was put on a train for Paris. Soon after their reunion, his father was arrested by the French Vichy police and put in an interment camp called Vernet in the Pyrenees Mountains near the Spanish border. As a consequence of the Vichy anti-Jewish legislation of 1940, Sasha was soon sent the Drancy internment camp before being handed over to the Nazis for deportation to Auschwitz where he was murdered in 1942.

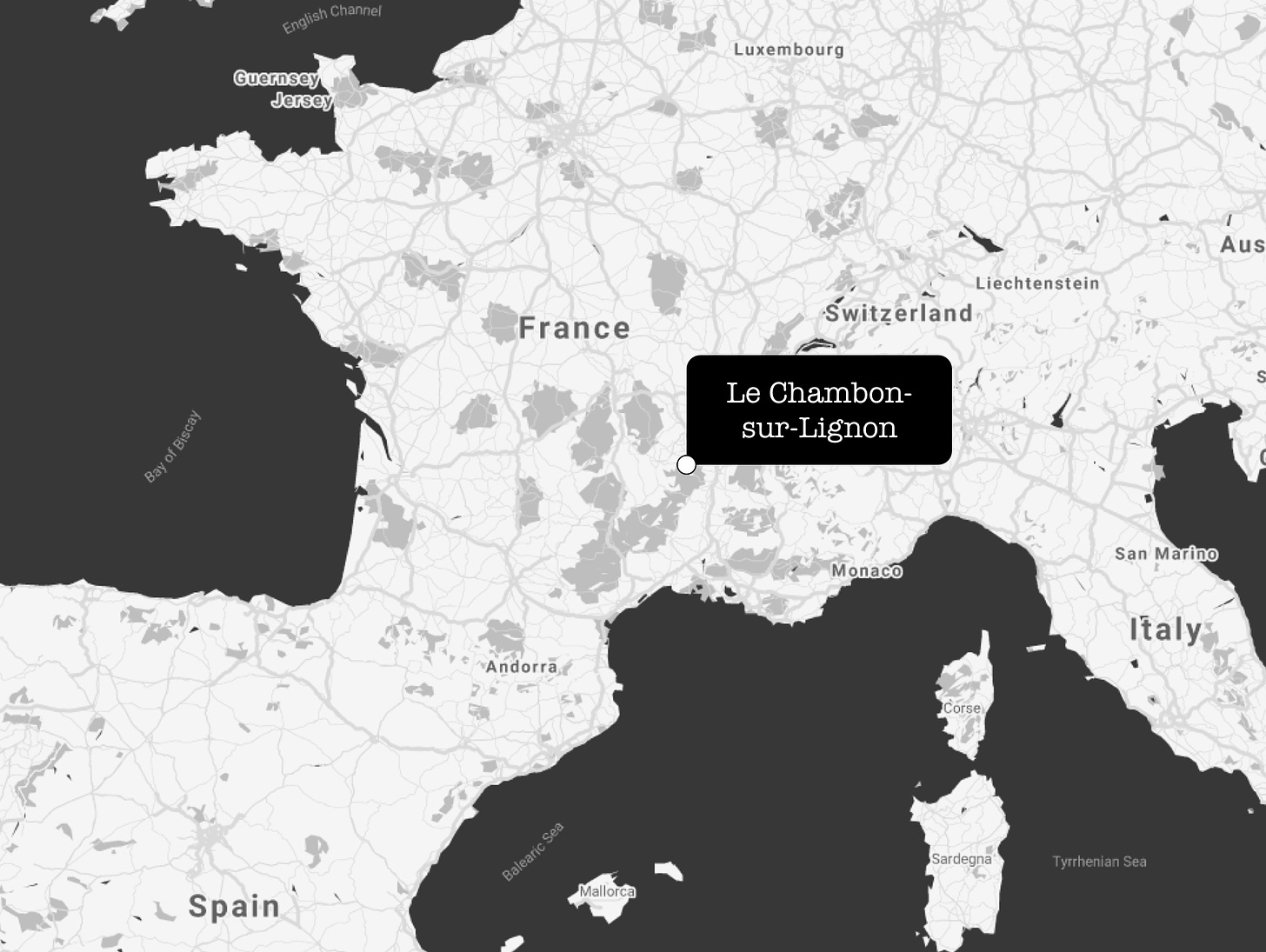
The town Grothendieck hid in during war.

Around the same time as Sasha’s arrest in 1940, Alexander and his mother were moved to the Rieucros Camp near the city of Mende in the south-east of France as “undesirable dangerous foreigners” (Pragacz, 2004). At 13 yeras old Alexander managed to escape the camp, but was soon taken back. The two were separated when Hanka was later transferred to the Gurs internment camp in the Pyrenees Mountains. Alexander, then 13 years old, found shelter in a hostel for refugee children called Secours Suisse, routinely having to flee into the forrest during Gestapo raids:

“Quand on était averti par la police locale qu’il y aurait des rafles de la Gestapo, on allait se cacher dans les bois pour une nuit ou deux, par petits groupes de deux ou trois, sans trop nous rendre compte qu’il y allait bel et bien de notre peau“ — From Récoltes et Semailles (Grothendieck, 1983–86)

Alexander was able to continue his education at the school now known as Le Collège-Lycée Cévenol International, then run by local Protestants pacifists and anti-war activists in the mountain town of Le Chambon-sur-Lignon.

“Chaim Honig once asked Grothendieck why he had gone into mathematics. Gothendieck replied that he had two special passions, mathematics and piano, but he chose mathematics because he thought it would be easier to earn a living that way” (Jackson, 2004a)

Education (1942–53)

Le Collège-Lycée Cévenol International (1942–44)

Alexander first discovered his passion for mathematics in his early teens, while attending the Le Collège-Lycée Cévenol International in south-eastern France, stating in his later autobiography Récoltes et Semailles that he “learned from an inmate, Maria, the definition of the circle [the set of points located at the same distance from a point]. It had impressed me with its simplicity and its obviousness, whereas the perfect roundness of the circle appeared to me as a mysterious reality”.

Even while still only in his early teens, Grothendieck was notoriously curious about the nature of geometry. As retold by Piotr Pragacz (2004), he was barely thirteen years old when he questioned to himself “How do you accurately measure the length of a curve, area of a surface and volume of a solid?“

Université de Montpellier (1945–1948)

“In Grothendieck’s days, […] not a proper place for studying great mathematical problems”— Jean Dieudonné (1990)

By the time the war in Europe ended in 1945, Grothendieck was 17 years old. He was reunited with his mother Hanka and the two went to live in a village outside of Montellier, where he enrolled at Université de Montpellier. There, he was awarded a scholarship which him and his mother survived on, in addition to her doing housework and him doing seasonal work in the grape harvest of the local wine fields (Jackson, 2004a).

Grothendieck did not blossom in Montpellier, as he found the lectures at the university to be uninspired repetitions of textbooks. Rather than attend, he would instead devote most of the three years of his undergraduate studies catching up on what he had missed in high school. This included “providing a satisfactory definition of length, area and volume” (Jackson, 2004a), which in essence involved re-discovering for himself the result known as the Lebesgue measure, first proved in 1902. Regarding his time there, Grothendieck himself later wrote

“I learned then, in solitude, the thing that is essential in the art of mathematics — that which no master can really teach”

École Normale Supérieure (1948–1949)

After Montpellier, Grothendieck continued on to Paris, where he spent a year attending courses at the prestigious École Normale Supérieure, the foremost research institution for mathematics in France at the time. His teacher of calculus in Montpellier, Monsieur Soula, recommended Grothendieck travel there and make contact with his former professor Élie Cartan (1869–1951), the father of the Professor Henri Cartan (1904–2008) at École Normale Supérieure (ENS).

Before he left, Grothendieck applied for a scholarship which required an interview with a French education official. The official later recalled being “astounded” at his meeting with the young Grothendieck:

“Instead of a meeting of twenty minutes, he went on for two hours explaining to me how he had reconstructed, ‘with the tools available’, theories that had taken decades to construct. He showed an extraordinary sagacity” — André Magnier

The official noted that he immediately recommended Grothendieck for the scholarship. He also noted, however, that he had been left with an impression of “an extraordinary young man” who already then appeared “imbalanced by suffering and deprivation”.

Grothendieck arrived in Paris in the fall of 1948. He began attending lectures in a legendary seminar held by Henri Cartan on algebraic topology and sheaf theory. There, he encountered for the first time many of the most prominent French mathematicians of the day, including Chevalley, Delsarte, Dieudonné, Godement, Schwartz and Cartan’s student, later Fields Medal winner Jean-Pierre Serre (Jackson, 2004a). Early leader of the Bourbaki group André Weil (1906–1998) also attended the seminar. Grothendieck, who had never before mingled with first-rate mathematicians was an outsider in the group. Not only was he a German in post-war France, his background as an undergraduate student from the Université de Montpellier was also sharply in contrast to that of the other attendees, most of which had their educational background from the prestigious ENS.

Despite this, as Jackson (2004a) writes, Grothendieck later recalled not feeling intimidated, but rather receiving what he called a “benevolent welcome” (Grothendieck, 1986 pp. 19–20) where he felt free to ask questions, but also found himself “struggling to learn things that those around him seemed to grasp instantly […] like they had known them from the cradle”. The contrast lead Grothendieck to eventually leave Paris, in October of 1949 on the advice of Cartan and Weil who recommended he instead travel to Nancy to work with Schwartz and Dieudonné on functional analysis.

University of Nancy (1950–53)

Although not as prestigious as the ENS in Paris, Nancy was indeed still one of the most prominent centers of mathematics in post-war France, having been central in birthing the Bourbaki movement. Studying under Laurant Schwartz (1915–2002), in Nancy Grothendieck immersed himself in functional analysis. Starting in 1950, his early papers (written starting when he was 22 years old) posed important questions regarding the structure of locally convex linear topological spaces such as the complete linear metric spaces. Grothendieck worked so hard during this period that his supervisor Schwartz reportedly told another graduate student, Paulo Ribenboim, “You seem to be a nice, well-balanced young man; you should make friends with Grothendieck and do something so that he is not only working” (Jackson, 2004).

His efforts paid off. During his time in Nancy, Grothendieck published an astounding six papers before completing his Ph.D.:

All six papers regarded the theory of function spaces spearheaded twenty years before by Polish mathematician Stefan Banach (1892–1945).

Dieudonné and Schwartz were running a seminar in Nancy on topological vector spaces. As Dieudonné explained, by this time Banach spaces and their duality were well understood, but locally convex spaces had only recently been introduced, and a general theory for their duality had not yet been worked out. In working in this area, he and Schwartz had run into a series of problems, which they decided to turn over to Grothendieck.

They were astonished when, some months later, he had solved every one of them and gone on to work on other questions in functional analysis.

- Excerpt, Comme Appelé du Néant - As If Summoned from the Void: The Life of Alexandre Grothendieck by Allyn Jackson (2004a)

“When, in 1953, it was time to grant him a doctor’s degree, it was necessary to choose from six papers he had written, any one of which was at the level of a good dissertation” Dieudonné (1989) later wrote. For his Ph.D. thesis, dedicated to his mother Hanka, Grothendieck chose a 1952 paper which would later be published as:

In the paper, starting from the Schwarts kernel theorem, Grothendieck proposes the notion of a nuclear space, which was later shown to have wide applications. Nuclear spaces are topological vector spaces whose properties have much in common with finite-dimensional vector spaces. That is, the topology on nuclear spaces can be defined by a family of seminorms whose unit balls decrease rapidly in size.

Left: Grothendieck in 1951 (Photo: Paulo Ribenboim). Right: The first page of Grothendieck’s Ph.D. thesis “Produits tensoriels topologiques et espaces nucléaires” in Séminare N. Bourbaki (1954)

His supervisor Schwartz later made Grothendieck’s graduate work the topic of a Paris seminar entitled Les Produits Tensoriels d’Après Grothendieck (“Tensor Products after Grothendieck”). Writer/mathematician Leila Schneps (1961-) who later communicated with Grothendieck, described his ascent to stardom during his time in Nancy as ‘incredible’ and ‘unique’, later writing:

He was so completely unknown to this group and to their professors, came from such a deprived and chaotic background, and was, compared to them, so ignorant at the start of his research career, that his fulgurating ascent to sudden stardom is all the more incredible; quite unique in the history of mathematics.

- Excerpt, Who Is Alexander Grothendieck: Anarchy, Mathematics, Spirituality, Volume 2, Chapter 3: From Student to Celebrity (1949-1952) by Leila Schneps (2012)

Career (1953–1970)

“When algebra and geometry were separated, their progress was slow and their use limited; but once these sciences were united, they lent each other mutual support and advanced rapidly together towards perfection.” — Joseph-Louis Lagrange (1795)

Historians often cite the fifteen year period from 1955–1970 as Grothendieck’s most prolific. During this period he would travel the world, win the most prestigious award in mathematics, involve himself in political causes and eventually be hired as a research professor at France’s version of the Institute for Advanced Study in Princeton, the Institute des Hautes Études Scientifiques outside of Paris.

A complete list of Grothendieck’s 103 published works is available here thanks to the Grothendieck Circle project initiated by Leila Schneps.

At the University of São Paulo (1953–1955)

Having completed his Ph.D. in a purely theoretical topic and being stateless (his passport and birth certificate were lost during the war) left Grothendieck with few prospects for employment after his graduation in 1953. As becoming a French citizen would have entailed mandatory military service, Grothendieck instead obtained a Nansen passport. This enabled him to travel to Brazil, where his Ph.D. supervisor Schwartz had recommended him for a visiting professorship at Universidade de São Paulo. He left in 1953.

While there, Grothendieck taught a course on topological vector spaces, the notes from which were subsequently published as Espaces vectoriels topologiques by Universidade de São Paulo. He also planned to write a book on topological vector spaces, but it never materialized. Grothendieck himself in his autobiographical writings Récoltes et Semailles described the period, especially 1954 as l’année pénible (“the wearisome year”) due to a lack of progress on the so-called “approximation problem” in topological vector spaces, a problem which was first posed in Stefan Banach (1892–1945)’s famous 1932 monograph Théorie des opérations linéaires (“The Theory of Linear Operations”). Famously, in 1936 Stanislaw Mazur had offered a live goose for the solution of the problem. Despite his best efforts, Grothendieck’s efforts never won him the goose.

Around the same time however, as a student in Grothendieck’s course later recalled, he began talking about changing fields. He was “very, very ambitious”, the student said (Jackson, 2004a):

“You could sense that drive — he had to do something fundamental, important, basic” — José Barros-Neto

Reportedly, even as early as in 1952, Grothendieck had told his contemporary Bernhard Malgrange that “there is nothing more to do”, the field of topological vector spaces is now “dead” (Jackson, 2004a).

At the University of Kansas (1955–56)

In 1955, Grothendieck received an offer to do research at the University of Kansas in Lawrence, at the invitation of Nachman Aronszajn (1907–1980) who also worked on function spaces in the 1950s (Colmez & Serre, 2003). His arrival on January 11th was announced by the Kansas University News Bureau:

Alexandre Grothendieck, brilliant young French mathematician, has arrived at the University of Kansas for a six months assignment as a visiting research associate professor. Grothendieck is an expert on the theory of linear topological spaces. A large research project, partially government sponsored, has been in progress at K.U. in that field for several years.

We sought Professor Grothendieck’s services a year ago as he was highly recommended by the best French mathematicians,” said Dr. G. Baley Price, department chairman. “However he was still on a 2-year engagement in São Paulo, Brazil.

By the time of his arrival in Kansas, Grothendieck had fully decided to change subjects and move towards topology and eventually, algebraic geometry. His letter to Jean-Pierre Serre dated January 28th, 1955 conveys his fervour at this time:

Letter from Grothendieck to Serre (January 28th 1955)
Dear Serre. A really annoying thing has happened: as I could not carry all my papers on the plane, I sent part of them in two packages, which were posted together the day I left. But only of them has arrived, a week ago, and by now it is unlikely that the other will arrive. 

It contained (among other things) those lectures from the Schwartz, Cartan and Cartier seminars thatt existed at the time, your paper on algebraic sheaves and the Kodaira-Spencer papers. I am very upset about this, as it will probably not be possible to replace the last to for some time, and I had not even had time to glance at Kodaira-Spencer. 

In any case, send me the complete set of all the lectures from all three seminars, if there are any left. I hope Barros remembers to bring you the Schwartz lectures. Can you also tell Spencer I have not received any of the papers he wanted to send me from Princeton?

[...]

My address is:
Dep. of Math., University of Kansas, Lawrence (Kansas) USA

Thank you in advance for your help. Yours, A. Grothendieck.

Serre and Grothendieck, while very different both as mathematicians and human beings, enjoyed a long and fruitful correspondence, the surviving letters from which were later published under the title Grothendieck-Serre Correspondence (Colmez & Serre, 2003). In his later autobiographical writings Grothendieck describes that most of what he learned in geometry — that he didn’t learn from self-study — he learned from his correspondence with Serre, calling him a “detonator” who provided the sparks that set ablaze explosions of ideas (Jackson, 2004a). By 1957, Grothendieck was fully immersed in problems in algebraic geometry and homological algebra, fueled in part by his correspondence with Serre (Cartier et al. 1990):

“The year 1955 marked a crucial change in my mathematical work: the passage from “analysis” to “geometry”. I still recall the striking (but of course entirely subjective) impression of leaving rude and arid steps, only to find myself suddenly in a sort of “promised land” filled with luxurious riches, multiplied everywhere to infinity, so that it suffices to lay your hand anywhere you like to gather and explore.”

Left: Grothendieck in Chicago, around 1955 (Artin et al, 2016). Right: The first page of Grothendieck’s “Tôhoku paper”

Indeed, while still in Kansas, Grothendieck had been able to put homological algebra on an axiomatic basis by introducing the abelian category concept (Pragacz, 2005). The results were published in a paper now referred to as the “Tôhoku paper”, which is actually entitled:

An English translated version is available here. The paper, which later contributed to his winning of the Fields Medal (1966), regards homological algebra, a purely algebraic aspect of algebraic topology. Considered a revolutionary paper, its results removed the need to distinguish between cases of modules over rings and the sheaves of abelian groups over topological spaces. The work extended the work of both Cartan and Samuel Eilenberg (1913–1998) on modules.

At Centre National de la Recherche Scientifique (1956–57)

Prior to traveling to Kansas, Grothendieck had in 1954 applied for a temporary position at Centre National de la Recherche Scientifique (CNRS) in Paris, only to be rejected. Whiles still in Kansas, Grothendieck applied again and the news of his acceptance arrived in Kansas in May of 1955. And so, Grothendieck returned to Paris in 1956. Once there, he spent most of his time regularly corresponding with Serre and continuing his work in topology and algebraic geometry. Borel later recalled him “bubbling with ideas” (Jackson, 2004a) at the time:

“I was sure something first-rate would come out of him. But then what came out was even much higher than I had expected. It was his version of Riemann-Roch, and that’s a fantastic theorem. This is really a masterpiece of mathematics”

In its classical form, the Riemann-Roch theorem is described as an important theorem which enables the computation of the dimension of the space of meromorphic functions with prescribed zeroes and poles. That is, it relates the complex analysis of a connected, compact Riemann surface to the surface’s topological genus, such that it can be handled as purely algebraic expression. The theorem was first proved by Riemann in 1857, before being refined for Riemann surfaces by his student Gustav Roch (1839–1866) in 1865. Then, as stated by Nick Katz of Princeton University, 90 years later:

“Grothendieck came along and said, ‘No, the Riemann-Roch theorem is not a theorem about varieties, it is a theorem about morphisms between varieties […] a fundamentally new point of view, the vary statement of the theorem completely changed”

Whereas the Riemann-Roch theorem relates the Euler characteristics of the cohomology of a vector bundle with their topological degrees for curves and line bundles, the Grothendieck-Riemann-Roch theorem changes the theorem from a statement about a single vector bundle to a vector bundle applying to chain complexes of sheaves. The achievement was later described by Borel as being “in the spirit of categories and functors”, but that “no one had ever thought about doing this in such a hard topic”, noting that (Jackson, 2004a)

“If people had been given that statement and had understood it, there might have been others who would have been able to prove it. But the statement itself was ten years ahead of anybody else”

Grothendieck’s unexpected but successful proof of his generalization of the celebrated Riemann-Roch theorem introduced what Grothendieck himself called K-groups, which provided the starting point for the development of topological K-theory, which helped both Grothendieck and his friend Michael Atiyah (1929–2019) win the Fields Medal in 1966.

At the Institute des Hautes Études Scientifiques (1958–1970)

“For twenty-five years, between 1945 and 1969, I invested practically my entire energy into mathematical research.” — Alexander Grothendieck

In 1958, on the strength of his work up until that point, Grothendieck was appointed a research professor at the newly founded Institute des Hautes Études Scientifiques (IHÉS) in Bures-sur-Yvette, just south of Paris. Founded by a businessman with a Ph.D. in Physics, Léon Motchane — with the moral support of J. Robert Oppenheimer — the IHÉS was envisioned to be French version of the Institute for Advanced Study in Princeton. According to historian David Aubin, Motchane first personally persuaded Dieudonné to join, who agreed only if he would also give an offer to Grothendieck. They both officially joined INÉS in March of 1959.

Grothendieck lecturing during his Seminaire de Géometrie Algebrique (SGA) at the IHÉS in the 1960s (Photos: IHES)

Among his first initiatives as professor, Grothendieck in May of 1959 started a seminar on algebraic geometry later referred to simply as SGA, Séminaire de Géométrie Algébrique du Bois Marie, and authored the first volumes of what is now considered a foundational work in modern algebraic geometry, the Éléments de Géométrie Algébrique(EGA) with contributions by Jean Dieudonné. According to former director of IHÉS, at the time of his death in 2014, the institute still sold over 100 copies of the latter, every year.

Around the same time, he also visited Harvard University for the first time, in the fall of 1958. He had been invited by algebraic geometer Oscar Zariski (1899–1986) who wanted his students to be exposed to Grothendieck’s powerful new methods, which in one sense had superseded his own:

One of Zariski's deepest theorems was that the inverse image of every normal point under a proper birational morphism from one variety onto another is connected. Then Grothendieck came along and he reproved this result by a descending induction on an assertion on the higher cohomology groups with Zariski's theorem resulting from the H⁰ case.

This seemed like black magic.

- Excerpt, ‘My Introduction to Schemes and Functions’ in: Alexandre Grothendieck: A Mathematical Portrait by David Mumford (2014)

According to David Mumford (1937-) who was there, Grothendieck was a hypnotizing presence at Harvard. Engaging, energetic, always willing to schedule another lecture to explain his ever-expanding theories to those interested.

“He wrote so fast and fluidly on the blackboard, I thought it resembled the ‘grass writing’ that I had heard about in a lecture on Chinese calligraphy: writing like the waves in the grass as a gust of wind sweeps over it”

Grothendieck at the University of Montreal in 1970 (Photo: unknown)

After a later visit in 1961, in which Grothendieck and Tate ran a seminar on “existence theorems and the representability of various functors such as Picard schemes”, he communicated home to Serre that:

“The mathematical atmosphere at Harvard is ravishing, a real breath of fresh air compared with Paris, which is getting more gloomy every year. Here there are a fair number of intelligent students who are beginning to be familiar with the language of schemes and ask for nothing more than to work on interesting problems, which obviously are not in short supply”

The boost of energy that his Harvard visits provided Grothendieck led him to rework his seminar on algebraic geometry, by now populated by the leading lights of mathematics in Paris and from abroad (Jackson, 2004a). The seminar took place at IHÉS’ new campus in a park called Bois-Marie in Bures-sur-Yvette just outside of Paris.

Attendees in Grothendieck’s seminar walking to the seminar building (Photo: IHES)

In addition to his research and seminars, Grothendieck during this time also supervised young mathematicians towards their Ph.Ds. Because the IHÉS (like the IAS in Princeton) didn’t award degrees, these students typically came from other universities in Paris and other parts of France. Well-known students of Grothendieck include later Fields Medalist Pierre Deligne (1944-), Michael Demazure (1937-), Luc Illusie (1940-) and Jean-Louis Verdier (1935–1989). Among his students, Grothendieck developed a reputation for being kind, friendly and an excellent teacher (Jackson, 2004a):

“His lectures were so clear, and he made so many efforts to recall what was necessary, the prerequisites. [….] He took time to explain very simple examples showing how the machinery works” — Luc Illusie

The Fields Medal (1966)

Grothendieck was awarded the prestigious Fields Medal at the International Congress of Mathematics in Moscow in 1966, two years before his 40th birthday. He won the award for his contributions which, according to the committee:

“Built on work of Weil and Zariski and effected fundamental advances in algebraic geometry. He introduced the idea of K-theory (the Grothendieck groups and rings). Revolutionized homological algebra in his celebrated ‘Tôhoku paper’.”

His co-recipients were Michael Atiyah (1929–2019), Paul Joseph Cohen (1934–2007) and Stephen Smale (1930-). Grothendieck refused to attend the ceremony for political reasons and so the IHÉS’ Director Léon Motchane traveled to Moscow to collect the medal in his stead.

Resignation (1970)

In late 1969 it had come to Grothendieck’s attention that the IHÉS was partially funded (never more than five percent) by grants from various sources within the French military. A staunch pacifist, Grothendieck had taken the matter to its founder and Director, Motchane. As the story goes, Motchane had agreed, but gone back on his words a few months later as the institute’s budget “stretched thin and he accepted a grand from the minister of the army” (Jackson, 2004a). Not alone in his opposition to the IHÉS’ acceptance of military funding, reportedly Grothendieck had prior to his resignation tried to convince his colleagues to threaten to resign alongside him. None did.

On the 25th of May 1970, at 42 years old, Grothendieck resigned his prestigious professorship at the IHÉS, effective at the latest, on October 1st. A letter confirming his wish to resign was sent to the Director of the IHÉS on June 9th.

Grothendieck’s letter of resignation (Scharlau, 2020 pp. 2)

Activism (1970–1985)

Photos of Grothendieck from his trip to Vietnam in 1967 (Photos: Hoàng Xuân Sinh)

A former prisoner of war, Grothendieck had been a strong opponent of the United States’ intervention in Vietnam, even visiting the country for three weeks in 1967. In his writings later he described the effect the trip had on him, “the many air raid alerts and bombing that left two mathematics teachers dead, as well as the valiant efforts of the Vietnamese to cultivate a mathematical life in their country” (Jackson, 2004b).

His first lecture following his resignation in the summer of 1970 was held at the Université de Paris in Orsay. A written version later circulated among Paris activists and students. The lecture, entitled Responsabilité du savant dans le monde d’aujourd’hui: Le savant et l’appareil militaire (“The responsibility of the scholar in today’s world: The scholar and the military apparatus”) discussed the threat of nuclear proliferation and claimed that conducting research funded by the military was harmful (Jackson, 2004b). Grothendieck’s activism continued throughout the 1970s. The same year as his departure, in collaboration with two other mathematicians he founded a political group called Survivre, later changed to Survivre et vivre. The grouppublished a bulletin dedicated to antimilitary and ecological issues, in the opposition of indiscriminate use of technology and science. Grothendieck served as its editor until 1973.

Erika Ifang’s brilliant 1988 portraits of Grothendieck

Twelve years later, in 1985, Grothendieck wrote a “beautifully written but bitter treatise” of about 1000 pages entitledRécoltes et Semailles (“Harvests and Seeds”), where he laid out his opposition and dissatisfactions with the mathematical community, which by that point he was all but entirely estranged from:

Grothendieck deeply resented the fact that, after he left the IHÉS, other mathematicians took up his ideas and carried them forward, adding their own imprint along the way. This resentment eventually metamorphosed into a paranoia which is evident in the pages of Récoltes et Semailles.

- Excerpt, The IHÉS at Forty by Allyn Jackson (1999)

He however continued to do mathematics, working for two years as a temporary professor at the Collège de France and finally as a professor at his alma matter, Université de Montpellier. His last position was as a researcher at Centre National de la Recherche Scientifique, where he worked briefly before being hired at the IHÉS. He formally retired from mathematics in 1988, continuing to live in a nearby village of Université de Montpellier by the name of Les Aumettes.

Grothendieck photographed by Erika Ifang in Les Aumettes in 1979

Seclusion (1991–2014)

In the work of discovery, this intense attention, this ardent solicitude, are an essential force, just like the warmth of the sun for the obscure gestation of seeds covered in nourishing soil, and for their humble and miraculous blossoming in the light of day. — Alexander Grothendieck

In the years prior to and following his retirement, Grothendieck began sending strange letters to former colleagues and friends, expressing his spiritual beliefs. For instance, in the period 1987–88 he wrote a 300-page manuscript (accompanying 500 pages of notes) entitled La Clef des Songes ou Dialogue avec le Bon Dieu (“The Key to Dreams or Dialogue with the Good Lord“) in which he expressed his conviction that “God exists and that he speaks to people through their dreams” (Jackson, 2004b). A few years later, in 1990, he wrote a letter entitled La Lettre de la Bonne Nouvelle (“The Letter of Good News”) which he addressed to 250 people, declaring that the “Age of Liberation will commence on the Day of Truth, 14 October 1996”.

Around the same time, he burned approximately 25,000 pages of his own writing, including various works in mathematics, letters between his parents in the 1930s and unpublished manuscripts in an attempt to “lighten himself of all things” (Jackson, 2004b).

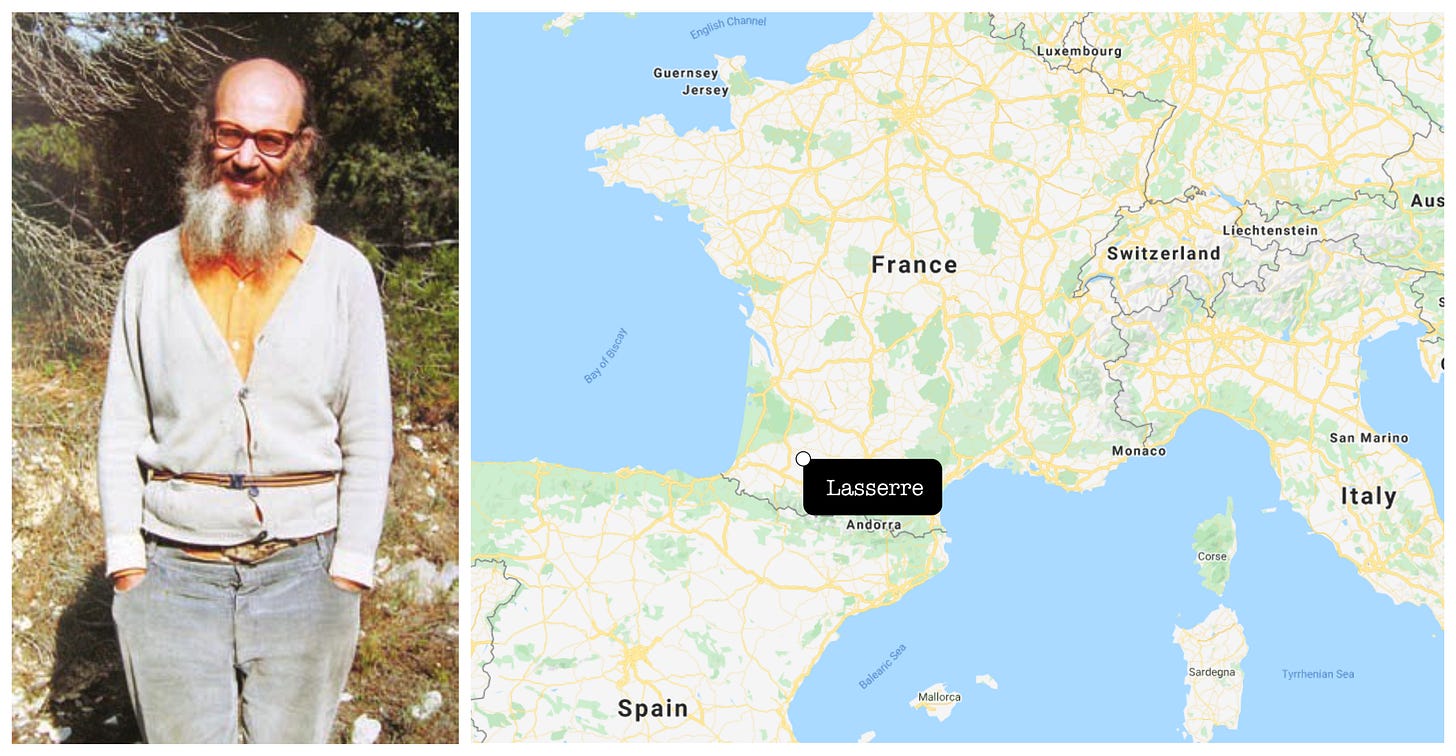
Already having abandoned the mathematical community, by the early 1990s Alexander Grothendieck was ready to abandon society all together. In 1991, without notifying anyone of his plans, he moved to the remote village of Lasserre in the Pyrenees Mountains of southern France. There, he lived for the next 23 years in isolation, partially supported by local villagers.

He died on November 13th 2014 at the age of 86 years old in the hospital at Saint-Girons.

Left: Grothendieck, year unknown. Right: Lasserre, where Grothendieck lived the last 23 years of his life in seclusion.

Legacy

Perhaps surprisingly, Alexander Grothendieck fathered five children. As Schnep (2020) later described, he was a “physically attractive man with a powerful, overwhelming personality” and so women often found him appealing, before feeling “deeply disabused and disappointed” shortly thereafter.

His firstborn, a son named Serge, was conceived with his landlady during his time as a graduate student in Nancy in the first half of the 1950s. Serge was raised largely by his mother, as Grothendieck left for Brazil in 1953. Grothendieck also had three children with his wife Mireille Dufour (who Grothendieck separated from in the early 70s): a daughter, Johanna, named after his mother in 1959, and two sons Alexander (1961) and Mathieu (1965). In addition, he fathered a child with a woman named Justine Skalba in the early 1970s, whom he lived in a commune with. According to biographer Winfried Scharlau (2020), like their father, neither of his children were able to “integrate successfully into mainstream society in what concerns education, profession, family or social circles”, writing “They are all “breakaways”.

Personality

“He was not mean, but very demanding of himself and everyone else”

Associates of Grothendieck who knew him during the 50s and 60s generally describe him as intense and demanding, such as Karin Tate, daughter of Emil Artin (1898–1962) and brother of Michael Artin (1934-):

“Extremely intense, seeing things in black-and-white with not shades of gray”, stating later that “You always knew where you stood with him. [He] didn’t pretend anything. He was direct”.

Her husband John Tate (1925–2019) however, described Grothendieck not as arrogant, but as “Just friendly, and at the same time rather naive and childlike […] Many mathematicians are childlike, unworldly in some sense, but Grothendieck more than most. He just seemed like an innocent — not very sophisticated, no pretense, no sham. He thought very clearly and explained things very patiently, without any sense of superiority.” A student who attended Grothendieck’s legendary IHÉS seminar described how “Grothendieck dominated whether he was the speaker or not. […] He was not unkind, but also not coddling”. Fellow Ph.D. student named Paulo Ribenboim (1928-) who arrived in Nancy around the same time as Grothendieck later recalled how despite his genius Grothendieck was “not the guy who would admit he didn’t understand” something (Jackson, 2004a).

Grothendieck is also remembered as extremely hard-working, by Barry Mazur (1937-) who described how arriving at his house late at night was never a concern: “We would take the last train back, absolutely certain that there would be Grothendieck working, his desk by the window.“ Similarly, David Ruelle expressed how “Grothendieck was working on the foundations of algebraic geometry seven days a week, twelve hours a day, for ten years”.

At the time of his death in 2014, mathematicians David Mumford and John Tate were asked to write an obituary for him for Nature magazine. It can be accessed in its entirety on Mumford’s website here.

Gunter Demnig’s Stolpersteiner placed in front of the childhood home of Grothendieck at 165 Brunnenstraße in Berlin, where the family resided from 1928–1933 (Photo: Berliner Mathematische Gesellschaft e.V.)

Those interested in reading more about Alexander Grothendieck are encouraged to read Allyn Jackson’s wonderful two-part article, which this essay is based on:

I also encourage those who are mathematically inclined to look up the beautiful book Alexandre Grothendieck: A Mathematical Portrait*, edited by Leila Schneps.

References

* This is an Amazon Affiliate link

Read more