When we look at the operation of integrating a function, we find that it resembles the operation of addition in the sense that it’s kind of an infinite sum of infinitely small numbers.

How much are these operations alike? and in particular, can we find a relation between them?

This article answers this and gives you one of the most powerful tools of analytic number theory: The Abel Summation Formula.

I will give you several examples of the formula in action along with some powerful notation to do asymptotic calculations. This notation is known as “big O” notation.

Let’s get started.

The Formula

The formula in all its generality is very general. I will state two special cases of it here that is very applicable but not as general as they could be. It is however enough for this article.

We need to introduce some notation.

By [x] we mean the integral part of x (sometimes called the integer part of x), i.e. the greatest integer smaller than or equal to x. By {x} we mean the fractional part of x defined by x = [x] + {x}.

The Abel Summation formula is the following. Let f be a continuously differentiable function, then

So this is a way of transforming a sum into an integral which we might be better at calculating. To be fair the integral is much like a sum because the function [t] is piecewise constant.

Asymptotics

The next thing I need to introduce to you is called “Big O” notation and is a genius piece of notation as I will show you in a bit. The notation is as follows:

When we write that, what we mean is that there exist constants K and c such that

In other words, f is bounded by some multiple of g in the limit. Another way of looking at it is that the ratio f/g eventually becomes a bounded function.

The Harmonic Numbers

The harmonic numbers are defined by the following sum.

They turn up in a lot of places, especially in number theory. What we want to do is to figure out approximately how these numbers grow.

We apply the Abel summation formula to the harmonic numbers with f(n) = 1/n.

The constant 1- C is sometimes called the Euler-Mascheroni constant and is denoted γ.

We have the following result.

Note that since 1/x → 0 as x → ∞ , we have that

γ turns up in a lot of places in analysis and is a very important number. Despite this, we don’t know much about it. We don’t even know if it is rational or irrational! One can calculate it to as many decimal places one wants and one gets γ ≈ 0.5772156649.

Triangular Numbers

The Greeks knew of these numbers and at that time (500BC–300BC) they tended to think about numbers geometrically. Therefore the triangular numbers, which I will define in a moment, were especially pleasing to them and they even knew of a proof of a certain polynomial formula, what we now call a closed-form expression that would generate them.

The first few numbers are the following:

1, 3, 6, 10, 15, 21, 28, …

They are the sums of the first n natural numbers i.e.

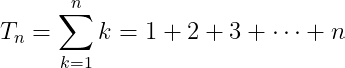
Why are they called triangular numbers? Well, you can view the sum as a triangle where the different terms in the sum correspond to the different layers in the triangle as in the following picture.

So how do we find a formula that generates them? Well, most proofs of such a formula “guess” the formula first and then proofs it to be true by induction afterward.

We shall take a different approach given the topic as I am sure that you’ve already guessed. We will find the closed-form expression formula by Abel summation. Of course, we will have our function f to be the identity i.e. f(n) = n. Assuming n is an integer we have:

At this point, you’re probably thinking that we’re stuck with this nasty integral but in fact, this is easy since if you think about it {t} is a periodic function cutting out a triangle with an area equal to half the area of the unit square on all whole number intervals throughout the real line.

Thus, we have

We have now proved that

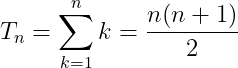
You can try it yourself and see if you get the above numbers.

The Riemann Zeta Function

Consider the partial sums of the famous series for the Riemann zeta function. If we apply Abel summation on that we get an interesting result.

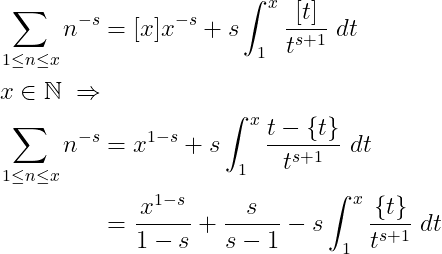
Assume that Re(s) > 1 so that we can take the limit x → ∞ on both sides. Then we get:

This is amazing. First of all, now we can see where the pole of zeta at s=1 comes from. Second, this is actually an analytic continuation of “the zeta function defined as a series" because the right-hand side converges for Re(s) > 0. This means that we can check the non-trivial zeros of zeta (we know that they don’t lie on the line s=0).

Abel Summation on Taylor Series

For the last example, I will show you a very interesting way to write the natural exponential function.

Before doing this though I need to introduce two special and very important functions, namely the gamma function Γ(z) and the digamma function ψ(z). Now, the gamma function has the following property: Γ(z+1) = zΓ(z) which makes it a generalization of the factorial. One can prove by induction that Γ(n) = (n-1)!. The digamma function is the logarithmic derivative of the gamma function and satisfies ψ(z+1) = ψ(z) + 1/z. They are defined by the following.

The gamma function can be extended to the whole complex plane by a very simple analytic continuation except at the non-positive integers where it has poles (i.e. blows up).

Recall the exponential function’s Taylor series:

By a few tricks followed by applying Abel summation on this series (be careful! you need to differentiate with respect to the running variable and not x) and taking the limit, we get

Wow! Can this be right? Well, one property that the exponential function has and that we can check immediately is the invariance under differentiation. Let’s do it.

Now we do a substitution in the integral along with applying the properties of our special functions

which by the inverse Abel summation used on the version of Abel summation above where we sum from 0, corresponds to the series

So it is because of the transformation rules of Γ and ψ that the differentiation invariance holds. The equality between the series above really needs more justification because Γ is not defined at 0. However, we see that

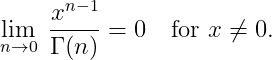
It is also clear that using this integral expression for the exponential function only works for x > 0 because of the logarithm. Maybe you can extend it?

Outro

The Abel Summation Formula is a powerful tool and it has been used to prove many interesting theorems. There are undoubtedly many more to be discovered using this formula.

I have chosen some series and sums that I find interesting but I suggest that you go and find your own sums. Transform them into integrals and see what you get.

Happy (Abel) summing.