Solving the Königsberg Bridge Problem

This proof is accessible to ANYONE — no mathematics knowledge required! (perfect for if you are a bit bored and in isolation, like me right now!)

The Königsberg bridge problem shows the beauty of mathematics to transform the impossible to the obvious. It also gives an insight into the mind of the genius Leonhard Euler.

Stating the problem

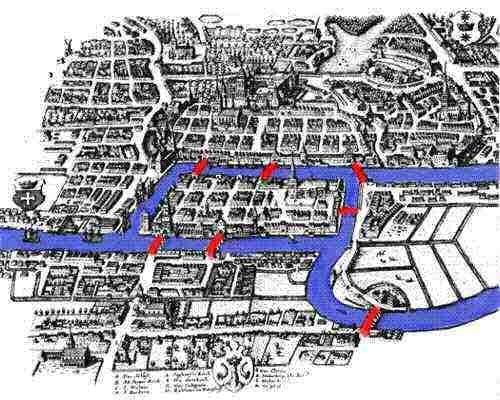
Have a look at the map above.

It’s a diagram of the rivers and bridges of Königsberg. The areas A, B, C and D are bits of land, joined by the bridges, but otherwise cut off from each other by water.

A map of the city is below. You can look at either diagram — both capture the key bits of information: which blobs of land are connected to which other blobs of land, and by how many bridges. In technical-speak, we are representing this as a graph. The blobs of land are the vertices, and the bridges are the edges. But that’s not important.

The problem is whether it is possible to find a route which goes over every bridge exactly once. That means, in our walk around the city, we want our route to go over every bridge, but it cannot cross over it two times, or three times… Basically, if you find yourself on the same bridge as you were previously, the path is invalid. If you finish your walk and there is a bridge you didn’t walk across, then your route was invalid.

The Solution

Consider each blob of land. Each bridge is connected to two blobs of land (that’s how bridges work). Each blob of land happens to have an odd number of bridges attached.

Now, let’s consider what a valid walk would look like.

As you go on your walk, you record in a notepad each time you are in a certain blob of land. For instance, if you start in the most southern end of the city, you make a note of that (take a photo, buy a souvenir…) and if you find yourself there again, you increase the tally for the southern sector to two.

For each blob of land there are two cases

(1) this is a section of the city we neither start our walk in, nor do we finish our walk there

(2) this is a section of the city either start our walk in, or we finish our walk in, or both.

Clearly, there are at most 2 sections of the city of the second type. We cannot start in two places at once, nor can we finish in two places at once.

As there are four sections of the city, that means that there are at least two sections of the city, in our walk, which we neither end nor start in. Let’s pick one of them.

Whenever we go into that sector, we use up one bridge, and whenever we leave it we use another. But, each sector has an odd number of bridges attached to it! That’s a contradiction. To see why, recall that each sector has either 3 bridges, or it has 5 bridges attached.

If we are in the sector once, we can only use up two of its bridges. If we are in it twice, we would use up four of its bridges (or run out of bridges, if it only had three bridges). If we are in it three times, we would require 6 bridges, which we cannot have. So the requirement that we both enter and leave a sector of the city which is not our start or our end point contradicts the fact that the number of connecting bridges is odd for every sector.