Solving the Dirichlet Integral

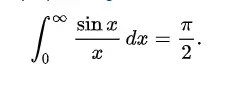
The Dirichlet integral was first solved by the brilliant Leonhard Euler (1707–1783), it then achieved fame with Peter Gustav Lejeune Dirichlet (1805–1859)’s work on Fourier series. Now it is our turn!

Part I: Approach

The main difficulty we have with this integral is the pesky 1/x attached to the sin(x).

Our strategy will be to ‘remove’ this, but introducing a new variable and solving a more general problem. Paradoxically, as is often the case in mathematics, solving the general case will be easier than solving the special case, as it will allow us to use more powerful tools from other parts of calculus.

The first thing we will define is a new function, whose variable is t.

How to make sense of this? You might even doubt this is a function! It doesn’t even look like a normal function. To dispel some doubts, here is a graph of I(t). As a computer cannot calculate upto infinity, I show the graphs that results with the upper bound of integration being a suitably large number.

While the formulas might not feel like a comfortable way to define a function, hopefully seeing the graphs puts you more at ease that we can define a function in this way. After all, for every value of t (horizontal axis), the function outputs a value of y (vertical axis).

Now, let’s look at t = 0:

That’s promising! If we worked out this new function, then we would just have to plug in t = 0 to get the value of the Dirichlet integral.

So, for different values of t, the function inside the integral changes, which in turn causes the value of the integral to change.

Part IIa: Limits

An important mathematical idea is that of a limit. A limit looks at ‘arbitrary closeness’.

Let’s look at a boring example. The limit as x tends to zero, often written using ‘lim’ and a right arrow:

lim x-> 0

is 0. To see why, look at the graph of f(x) = x

As the input, x, gets arbitrarily close to 0, so does the output f(x). Of course, in this case f(x) = x, so it is not surprising that as the input gets close, the output gets close, as the input and output of the function are the same.

Let’s look at a more interesting example. f(x) = x³. We want to know what the limit of f(x) is as x tends to 0. Again, we look at the graph:

and from the graph it seems obvious that as the input gets arbitrarily close to 0, so does the output.

We won’t go into an in depth exploration of how to define a limit rigorously here. What’s important is that limits can be applied sensible to more interesting mathematical expressions too. As we will see, the derivative is defined through a limit, which will allow us to crack what seemed at first to be an impossible integral!

Part IIb: Differentiation

Intuitively, differentiation looks at how small changes in the input divided by that change look like. More precisely, the derivative of our function I(t) is given by:

In the above, ‘delta’ [delta is the squiggly d] t represents a small change to in input value t, which we make arbitrarily small. You may be more comfortable with conceptualising the derivative as the gradient of a tangent line to a function at a point.

We can also differentiate e^(-xt) with respect to t.

What do we mean by ‘x is being held constant’? Well, suppose you are baking a cake. The fluffiness of the cake changes as you add more flour, but it also changes when you leave it in the oven longer. We might write fluffiness as a function of flour and oven time: F(flour, oven time). For any given oven time, say 25 minutes, the fluffiness now only depends on flour added. So we can look at the ratio of small changes in flour to the change caused in the fluffiness of the cake. The reverse is also true: you could decide in advance to only use 100g flour, and then the fluffiness will only change as the temperature of the oven changes. Therefore, given a function in two variables, we can keep one ‘fixed’ at some value, and treat it as a function of the remaining variable.

Part III: Solving the Integral

We start with the the function we defined previously:

And we take the derivative. Remember how this was defined?

We now go ahead, and plug in the function evaluated at t+delta t (a delta is the squiggly d), at t, and divide by delta t

Take some time to digest the above. In particular, can you see how the right hand side is just the definition of I(t + delta t) — I(t) divided by delta t? Have another look at the definition of I(t) if it doesn’t yet make sense.

To proceed, we go ahead and keep simplifying the right hand side of the equation.

That second step needs some justification. Why are we allowed to put the limit sign inside the integral? The answer actually goes into some quite deep analysis, which is normally justified using Lebesgue integrals. Instead, we take the approach of physicists, and wave it through, because it looks plausibly true, and the end answer is right.

Now that the limit is inside the integral, we can observe that this is, in fact, our definition of differentiation for e^(tx). But we know how to differentiate this! Somewhat magically, we now ‘disappear’ the 1/x factor mafia-style.

Now that the 1/x factor is disappeared, we can evaluate this integral. This can be done using ‘integration by parts’. Be aware that, when evaluating this integral, we are evaluating it with respect to dx so ‘t’ is treated like a constant.

I’m going to be honest. The integration by parts isn’t exactly pretty, and it’s fiddly to keep track of all the -1 factors*. However, it does illustrate a common trick in mathematics: you get some unknown quantity, and you find out how it is related to itself, and solve the resulting equation.

*Yes, I made several mistakes first time round!

In this light, feel free to skim over the first 2 equations, but the last three lines show how this trick is being used.

This allows us to conclude that:

What’s nice about this expression is that it has an exact solution! We just need to get the anti derivative (a.k.a the integral of) 1/(1+t²)

where c is the constant of integration. We are so nearly done! To evaluate the constant of integration, let’s look at what happens as t tends to infinity (yes! another limit)

Finally, we may gloriously conclude that

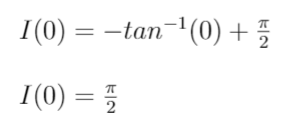
A wild journal with escapades through functions of two variables, limits and differentiation inside integrals, and more. I hope you enjoyed and found it interesting :)