Solving Infinite with Finite
Mathematics has a lot of hidden gems. Today I will try to give us a glimpse to one of the vast domain — modular arithmetics.
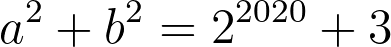
Mathematics has a lot of hidden gems. Today I will try to give us a glimpse to one of the vast domain — modular arithmetics.
In the last post, we showed that there are no circles at the origin with a finite number of rational points. We also said that no rational points are lying on a circle with a radius square root of 3, but we did not prove it. Before starting the proof, we need to get comfortable with one fundamental instrument of mathematics — modular arithmetic.

We can find usage of modular arithmetic in many different domains of mathematics: group theory, field theory, number theory, p-adic theory and many others. Carl Friedrich Gauss introduced modular arithmetic at the beginning of the 19th century when he was 21. His textbook “Disquisitiones Arithmeticae” was the first document formalizing the concept of residue classes and other crucial parts of modern number theory.
We can start with a real-world example. Modular arithmetics is often associated with the mechanism of clock hands. Because of that, sometimes modular arithmetics could be mentioned as a clock arithmetics. As an example, assume we know that short hour hand points to 9 and someone asked us what it will be pointing after 28 hours. It will not be a tough question for us, because we know that adding number, which is a multiple of 12, will not change the position of the clock hand. So we can take the remainder from division 28 on 12 which is equal to 4 and add it to 3 getting 1 hour.

Let us define a formal way of using modular arithmetic. To do it, we introduce a concept of congruent relation. Two numbers a and b are congruent modulo n if and only if n divides the difference of a and b

Let us take 66 and 21 as examples and compare them modulo 5. We can use the fact that every whole number a could be uniquely represented as follow,

where n, q and r are whole numbers. Let us write decomposition of 66 and 21 in that way

We can easily show that if we calculate the difference between these numbers, then their remainders will cancel out and we will get a number divisible by 5.

So as a corollary we have the fact that two numbers are congruent modulo n if their remainders are the same when n divides them.
We can use the steps from above for any two numbers to understand whether they are congruent or not. That way, we can create the relation defined on every pair of whole numbers. It is simple to show that this relation will be:
- Reflexive — any number a is congruent to itself.
- Symmetric — if a and b are congruent, then b and a are too.
- Transitive — if a and b, b and c are congruent, then a and c are too.
If any relation defined on the set of objects has these three properties, it could be called an equivalence relation and whole set of objects could be split into equivalence classes. In our case, we will identify every class by the remainder from the division by n. There are exactly n distinct remainders so that we will have exactly n distinct classes. We will use the notation [a] for the class of number a,assuming the value of n from the context. We can think about these equivalence classes as values of the clock hands from our real-world example.
Mapping from a to [a] is a function from the set of whole numbers to the set of all remainders from division by n. To continue, we need to understand the two main properties of this function.

These properties tell us that our function is a homomorphism. This word may sound scary, but it just says that our function conserves all operations after mapping. Try to prove it as an exercise; it is not so hard as it seems. If we apply this function to any polynomial, we can get quite curious results. Let us take this one as a primer.

Assume that this polynomial equation has a solution in the whole numbers, then we can apply our mapping defined earlier to it and get a solution in terms of residue classes. Let us take n equal to 2 and apply our homomorphism to this polynomial equation.

From first glance, nothing changed, but remember that [x] can have only n different values. In our case n is equal to 2, and it allows us to substitute every possible value of [x] to check equality. If we do not find values that satisfy the equation, it will mean that our initial equation can not have the whole solutions too.

This example is not very interesting, because we can use school method to solve it and understand that there is no solution even in the real numbers. Let us look at more interesting one. Try to find a and b such that:

We can use our function again with n equal to 4 to see whether it helps us.

The right side of the equation could be simplified.

Let us substitute every possible value of [a] on the left side.

We can see that there are no combinations of [a] and [b] that could give us [3] as a sum, so this equation cannot have solutions in the whole numbers.
Sometimes using this technique, we can reduce an infinite number of tries to a small few. Next time I will use this technic for proving that there are no rational points on the circle with a radius square root of 3.





