Solving a Handshaking Problem using Recursion

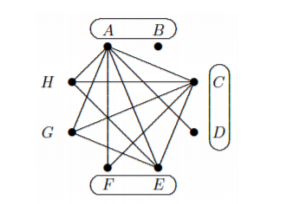
Statement of the problem

Mr. and Mrs. Bryan invite four other couples for dinner. At the beginning of the evening there is some hand shaking. Mr. Bryan notes that none of the nine other people shook the same number of hands. So how man hands did Mr. Bryan shake? How many did Mrs. Bryan shake? (Clearly one doesn’t shake hands with one’s spouse or one’s self.)

Approach

We are going to reduce this to a smaller problem, and then reapply the same logic every time. The idea is that we can remove someone from the ‘graph’ of handshakes and focus on the handshakes all the remaining people made. We can do this, and keep track of how many hands Mr and Mrs Bryan have made. In particular, we are going to ‘remove’ people from the graph of handshakes two at a time (in their couples, it turns out) after we have determined whether Mr and Mrs Bryan shook their hands. Then we will work out what the new handshake graph is like, and repeat, until we are done.

I say graph, because the mathematical object used to represent such problems is normally a graph. People in this case would be represented as vertices, and handshakes as edges.

Solution

Of those 9 people, one person shook 0 hands, one shook 1, one shook 2, … one shook 8.

One person shook 8 hands. Excluding themselves and their spouse, that must mean they shook everyone else’s hands. So, that person’s spouse shook zero hands. That means our protagonist shook at least 1 hand. Also, Mrs Bryan wasn’t removed, so she has shaken at least one hand.

Now, let’s remove that person and their spouse from the ‘graph’. This leaves 8 people, 7 other people, and our protagonist My Bryan. Every remaining person’s handshake count is reduced by one for this subset of people, as each one of them shook hands with the person who shook 8 hands. The person who shook the most hands therefore shook 6 hands. The same logic repeats, as this person must therefore have shook everyone but their own hand and their spouse’s hand. Our protagonists Mr and Mrs Bryan are now on 2 hands shook, and we are left with 6 people: our protagonist Mr Bryan and 5 others.

Now we remove the person in the paragraph above, and their spouse, from the handshake graph. These all see their handshake counts reduced by 1, as all of them shook the hand of the person who was removed, along with their spouse, in the previous paragraph. The top person shook 4 hands now. By the same logic, we can remove them and their spouse, Mr and Mrs Bryan is now on 3 total hands shook, and there are 4 people left.

Finally, we have four people, and one person, who was not Mr Bryan shook two hands of these four people, and so that person’s spouse shook 0 hands of these four. Adding in the final handshake By Mr Bryan ends up on 4 handshakes, and so does Mrs Bryan.