A Shannon cipher, invented by its namesake Claude Shannon (1916–2001) is a simplified cipher mechanism for encrypting a message using a shared secret key. A cipher is generally defined simply as an algorithm for performing encryption or decryption, i.e. “a series of well-defined steps that can be followed as a procedure”.

Example (Boneh & Shoup, 2020)
Suppose Claude and Marvin want to use a ciper such that Claude can send an encrypted message that only Marvin can read.Then, Claude and Marvin must in advance agree on a key k ∈ K. Assuming they do, then when Claude wants to send a message m ∈ M to Marvin, he encrypts m under k, obtaining the ciphertext c = E(k,m) ∈ C, and then sends c to Marvin via some communication channel. Upon receiving the encrypted message c, Marvin decrypts c under k. The correctness property ensures that D(k,c) is the same as Claude's original message m.

Regarded by many as the foundation of modern cryptography, the concept of a Shannon cipher was first introduced in the 1949 paper Communication Theory and Secrecy Systems published by Shannon in a Bell Systems Technical Journal. The results Shannon presented in the paper were based on an earlier version of his research in a classified report entitled A Mathematical Theory of Cryptography, and preceded Shannon’s publication of his well-known A Mathematical Theory of Communication published a year before, in 1948. The following discussion of Shannon ciphers is based on Chapter 2.1 “Shannon ciphers and perfect security” in the book A Graduate Course in Applied Cryptography by Dan Boneh and Victor Shoup.

Definition

Formally, a Shannon cipher is a pair of encryption (E) and decryption functions (D):

wherein in order to encrypt a message m:

Encryption
The encryption function E takes as input a key k and a message m, to produce a ciphertext c. That is, c = E(k,m), stated as "c is the encryption of m under k".

and in order to decrypt the encrypted ciphertext c:

Decryption
The decryption function D takes as input a key k and a ciphertext c, to produce a message m. That is, m = D(k,c), stated as "m is the decryption of c under k".

In order to ensure that the operation functions as intended, we require the following property of the cipher:

Correctness Property
Decryption "undoes" encryption, that is, the cipher must satisfy the following correctness property: for all keys k and all messages m, D(k,E(k,m)) = m, stated as "m is the decryption of E(k,m) under k"

One-time pads

In cryptography, a one-time pad (OTP) is an encryption technique that cannot be cracked (i.e. cannot be computed). It requires the use of a one-time key kwhich is shared prior to the transmission of a message. The key must be the same size as, or longer than the message being transmitted. Formally (Boneh & Shoup, 2020):

Definition of a one-time pad
A one-time pad is a Shannon cipher ε = (E,D) where the keys (k), messages (m) and ciphertexts (c) are bit strings of the same length.

That is, the one-time pad Shannon cipher ε is defined over (K,M,C), where

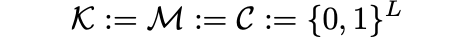
for some fixed parameter L. For a key k ∈ {0,1}ᴸ and a message m ∈ {0,1}ᴸ, the encryption function E(k,m) is defined as k ⨁ m = c, where ⨁ denotes component-wise addition modulo 2.

One-time pads work by pairing a message m in plaintext with a random secret key (referred to as a one-time pad). Next, each bit or character of the message is encrypted by combining it with the corresponding bit or character from the pad using modular arithmetic. If the one-time pad used fulfills the following properties: 1. It is truly random; 2. It is at least as long as the plaintext; 3. It is never reused in whole or in part; and 4. It is kept completely secret; then the ciphertext can be shown to be impossible to decrypt or break, i.e. “perfectly secure”.

Perfect Security

In cryptography the gold standard of security, “perfect security” is a special case of information-theoretic security wherein for an encryption algorithm, if there is ciphertext produced that uses it, no information about the message is provided without knowledge of the key. Formally (Boneh & Shoup, 2020),

Definition of perfect security
Let ε = (E,D) be a Shannon cipher defined over (K,M,C). Consider a probabilistic experiment in which the random variable k is uniformly distributed over K. If for all m₀, m₁ ∈ M, and all c ∈ C, we have:Pr[E(k,m₀) = c] = Pr[E(k,m₁) = c]then we say that ε is a perfectly secure Shannon cipher.

In words, the probability that a ciphertext c is m₀ is the same as the probability that the same ciphertext c is m₁, then the cipher ε is a perfectly secure Shannon cipher. That is, the perfectly secure Shannon cipher ε has produced a ciphertext which has equal probability of being any message, i.e. the ciphertext c gives no information about the plaintext m. In order to construct a proof that this is the case, we must first provide a few equivalences from Boneh & Shoup (2020):

Let ε = (E,D) be a Shannon cipher defined over (K,M,C). Then the following statements are equivalent:i) ε is perfectly secure;ii) For every ciphertext c ∈ C there exists Nc (possibly depending on c) such that for all messages m ∈ M, we have |{k ∈ K : E(k,m) = c}| = Nciii) If the random variable k is uniformly distributed over K, then each of the random variables E(k,m) for m ∈ M has the same distribution

That is, the statement that ε is i) perfectly secure is equivalent to the statements that ii) for every cipher c there exists a certain number of ciphers Nc such that for all messages m, the encryption function E can generate c

ii) for every cipher c, there exists a number Pc (depending on c) such that for all messages m, the probability that the encryption function E(k,m) generates the ciphertext c is Pc. Here, k is a random variable distributed over K and Pc = Nc/|K|, and iii) that if the random variable k is uniformly distributed over K, then each random variable k which may be used to encrypt m has the same distribution. The proof of these equivalences is available in Boneh & Shoup (2020, p. 9). From ii), we can next provide the following proof that one-time pads satisfy the requirements for a perfectly secure Shannon cipher:

Proof that the one-time pad is a perfectly secure Shannon cipher
Suppose the Shannon cipher ε = (E,D) is a one-time pad and is defined over (K,M,C) where K := M := C := {0,1}ᴸ. For any fixed message m ∈ {0,1}ᴸ and ciphertext c ∈ {0,1}ᴸ, there is a unique key k ∈ {0,1}ᴸ satisfying the equation k ⨁ m = cnamely, k := m ⨁ c. Therefore, ε satisfies condition ii) in theorem 2.1 above (with Nc = 1 for each ciphertext c).

Epilogue

Although symmetric cryptographic systems have been known for at least two thousand years (read: Caesar cipher), Shannon’s 1949 paper was the first to provide a formal mathematical description of such systems. In his paper, Shannon defined the properties of what he called “perfect secrecy” for shared-key systems and showed that they must exist.

Those interested in reading more about Shannon ciphers are encouraged to download the book A Graduate Course in Applied Cryptography by Dan Boneh and Victor Shoup (2020). Those interested in reading more about Claude Shannon are encouraged to acquire the book A Mind at Play: How Claude Shannon Invented the Information Age by Jimmy Soni and Rob Goodman.