Here’s a cute way to prove the existence of Transcendental numbers. It requires *only* a keenness for mathematics, and is combined with a quick guide to the infinite and Cantor’s Diagonalisation argument! We’ll also see that there are ‘more’ transcendental numbers than non-transcendental .

Below: Cantor’s Diagonalisation Argument in base 2. More on this later!

Step 1: What is a Transcendental Number?

A transcendental number is one which cannot be written as the root of a polynomial with integer coefficients. Numbers which are the root of a polynomial with integer coefficients are called algebraic.

Strangely, it is not so hard* to prove they exist, but very very hard to prove a number is transcendental. *comparatively speaking.

For instance, the square root of 1.5 is NOT transcendental because it solves the equation 2x² -3 = 0.

Whereas pi, famous pi, IS transcendental, because no polynomial with integer coefficients exists to which it is a root(although proving this is difficult and uses the Lindemann-Weierstrass Theorem). So we’ll tackle a slightly strange question. We want to prove that transcendental numbers exist without necessarily being able to give an example of one!

[A word on notation. (1) I will sometimes refer to polynomials with integer coefficients as algebraic equations. (2) A countably infinite list is one with an infinite number of elements but we can enumerate all of them. A little more formally, we can pair up elements in the list with the positive integers, so that for each element of the list it makes sense to ask which element of the list it is. The simplest example are the positive integers themselves: the 5th element of the positive integers is 5, the 6th element is 6, and, in general, the Nth element is N. Another way of looking at a countably infinite list is that it is a list which you will never reach the end, but by counting ‘upwards’ from an initial element, it only takes a finite amount of time to reach any particular element of the list. You cannot count ‘to infinity’, but given enough time you can count to 1 million.)

Step 2: there are only a countably infinite number of algebraic numbers

(N.B. We use Cantor’s Diagonalisation argument in Step 3).

Countably infinite means that we, theoretically, create a list, and for any algebraic number you cared to name, we could point at its position on the list. This section can be a bit tricky on first reading, so don’t worry if it’s a little confusing at first. If you feel too stuck at any point, you can take my word that this is true, and more onto step 2.

A helpful example: the integers are countably infinite

The integers are countable, for example. Consider the list (0, -1, 1, 2, -2, 3, -3, …)

Yes the list goes on forever, but if I gave you a number, maybe 50 or maybe -10¹⁰⁰⁰⁰⁰ you would eventually find it a finite number of elements into that list.

Pairs of integers are countably infinite

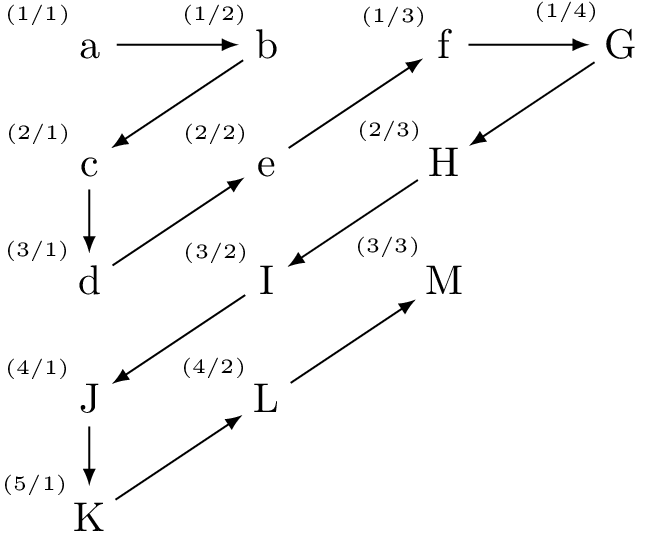
Before you read the below, let’s imagine you have a large square of people. You can count the group of people in several ways. You can count the people in several ways. You can count each column, and then count the number of rows. You can count each diagonal and sum them up.

The issue with an infinite grid, is that if you went counting down one of the columns, you’d never reach the end. Yes, you’d have proven that there are so many people that a subset of them is contained in a countable list, but you’d have failed to prove there was also a list including all of them.

Instead, we count along the diagonals. Fortunately each diagonal has a finite number of people. (See the diagram below). We can put all the diagonals in a countable list, and then find which diagonal an element is in.

This proves that there are a countable number of pairs of integers. If you hand me a pair of integers, it is a dot in the grid, and so is found in some diagonal, say in the Kth diagonal. But there are only 1+2+3+…+K elements in the first K diagonals, so this element will be found in the first K(K+1)/2 elements of our list. I.e. every possible pair of integers is found somewhere in our list.

For instance, if you gave me the pair (3,2), that’s found in the 4th diagonal, as the 4th diagonal contains all pairs whose sum is 5 (take a look at the diagram if you don’t believe me). We know that it is found in the first 1+2+3+4 elements, that’s 10, or 4*5/2 = 20/2 = 10, as I promised.

Triplets of integers are countably infinite

Now let’s pull off a blinder of a trick.

Now we’ve proven that all pairs of integers are countably infinite. But a triplet of integers is a pair of… an integer and a pair of integers! (In any case, they store the same information)

(a,b,c) = (a, (b,c))

As we managed to find a countable list containing all pairs of integers, this is the same problem as before, as we can look at our list of all possibilities for (b,). If we parcel up each distinct pair (b,c) with the label A, then we want to find all lists of the form (a, A), where A is an element from another countably infinite list. (No need to look under the hood of A, all we need to remember is that it is a countable list).

We can do the same AGAIN! If we want to consider all lists of the form (a,b,c,d) where a,b,c,d are all integers, we now treat this as (a,A), where A is one of the countably infinite list of triplets (b,c,d)! The we prove that all lists of 5 integers are countable similarly. Then lists of 6 integers. And so on and so on. This leads to…

All combinations of K integers are countably infinite

We prove this by dominoes. Well, by induction, which is basically the same thing.

If all (K-1) long lists of integers are countably infinite, we pull our same trick as before. We abstract away from the details of the list we found, and just use the fact that it is countable, and it is exhaustive, i.e. it goes through all possible combinations. Then, all combinations of (a, A) are exhaustive of lists of integers with K elements, as a K element can be decomposed into a first element, a, and the remaining list, which has K-1 elements.

This is basically a domino argument. Each case proves the next case, and so we can be sure that each domino falls, provided the first domino falls.

The number (‘cardinality’) of polynomials with integer roots is countably infinite. The number of roots to polynomials with integer roots is countably infinite.

We represent each algebraic equation as a list.

For instance, the equation 5x²-4x+2=0 can be represented as (5,-4,2).

Every algebraic equation has a ‘maximum term’. The maximum term of the above equation is x² , which has a coefficient of 5. The maximum term of x⁷+7x-9=0 is x⁷, which has a coefficient of 1. In general the term is the largest power of x with a non-zero coefficient.

We have all the algebraic equations whose maximum term is 1. That’s equations of the form ax+b=0. We can find a countable list which contains all these equations. As each of these equations has at most one solution, we can contain all solutions to such an equation in a countably infinite list.

The equations whose maximum term is 2 are quadratic equations of the form ax²+bx+c=0. All such equations with integer coefficients can also be found in a countable list. But all these equations have at most 2 roots (as, recall, we can factor polynomials to a product of x minus their roots). Therefore we get our list before, but instead write in the two solutions (or maybe one, or none for some equations) when previously we would have written in the equation. Thus, it takes us at most twice as long to reach a root of an equation as it took in our previous list to reach the equation but we still get there.

This continues. For equations with a maximum term of size k, we have at most k roots, and can pull off the same stunt: we get the countable list of all such equations, and then jam in the k roots. It may take upto k times as many steps to reach a root of an equation compared to how long it took to reach the equation in our original list, but we still get there in a finite number of steps.

Now we array a HUGE grid of points. This grid of points contains EVERY solution to an algebraic equation. The first row is our countably infinite list or all roots to algebraic equations of size 1. The second row is our countably infinite list of all roots to algebraic equations of size 2, and so on.

Using our previous trick, we go along the diagonals. This gives us a countable list containing all solutions to polynomials with integer coefficients.

Step 3: There are an uncountable number of real numbers.

Suppose your evil nemesis (the devil, stalin, your annoying younger sibling…) hands you a list containing all the real numbers. Can you prove that they are lying when they claim the list contains all the real numbers?

Sure you can.

You can construct a number not in their list. In fact,we can do this restricting ourselves just to a number less than one.

To construct your number, look at the first number in your evil adversary’s list. Now, pick your first digit, the digit for the ‘10ths’ column, to be different to its digit for the 10ths column. This is quite easy , as there are 10 digits to choose from, and they can only have used one.

Now, for the second digit, choose your 100ths column digit to be different from theirs. And so on.

With a few fiddly details (which don’t change the essence of the proof, and probably distract from it on a first reading), if your evil nemesis says, aha! my 7th, 102nd, 12048121st, or Nth digit is the number you constructed, then you can prove them wrong — after all, you chose your 7th digit to make it different from the 7th number in their list, and you chose your 102nd digit to make it different from their 102nd number, and, when you got there, you chose your 12048121st digit to make it different from their 12048121st number.

So there are no lists which contain all the real numbers.

Conclusion: There are transcendental numbers!

Combining our previous steps, we reach our conclusion!

We managed to show there are only a countably infinite number of algebraic numbers. In mathematical speak, we managed to show that their cardinality is ‘countable’. I.e. we could construct a list which contained all of them.

Then we showed that there is no countably infinite list which contains all the real numbers.

So, our list involving all the algebraic numbers must be missing a lot of real numbers (missing an uncountably many!).

Congratulations, you’ve just understood Cantor’s diagonalisation argument, one of the major advances in 19th century mathematics, along with cardinality arguments, and then applied it to a cute problem about transcendentals :)