Let’s prove a beautiful Theorem from complex analysis!! For the determined amateur with some knowledge of 12th grade math and calculus.

Some prerequisites

Here we give a feel for some of the key concepts underlying the proof.

Differentiation of complex functions

The Cauchy-Goursat Theorem is about the integration of ‘holomorphic’ functions on triangles. A holomorphic function is basically an extension of what differentiability means, but for complex numbers. Basically, we want the following expression to converge as h tends to zero.

However, as we are dealing with complex functions (i.e. a function which takes a complex number as an input, and a complex number as an output), the conditions are a little stronger than for real functions. That’s because the complex numbers are a plane: a 2-dimensional object. So our limit can come from any direction: left, right, up, down, spiral, you name it. Whereas in normal calculus, we can only approach a number, say 3, in a one-dimensional manner (i.e. from the left, such as 2.9, 2.99, 2.999, 2.9999, and from the right, such as 3.1, 3.01, 3.0001, 3.00001, …). So ‘holomorphism’ is a stronger requirement, but it has some wondrous consequences.

Integrating over curves

Also, we integrate over curves, rather than in real variable calculus, where we integrated over intervals. In real variable calculus you might have said: let’s integrate this function between 0 and 1, but in complex calculus you can integrate a function over a curve which connects, say, 2 + 3i and 1 + 6i.

Also, when we integrate over a curve, we don’t just get one output, we get two outputs: a real part and an imaginary part.

Anti-derivatives and evaluating integrals

An important continuity (ha-ha, sorry about the pun) with real analysis is that to integrate a function f along a curve C, if we find a function F which differentiates to it, then the integral of f along C is just F(w) — F(v) where w and v are the endpoints of the curve C. That means that it depends solely on the endpoints of the curve if we can find an anti-derivative.

A really really important consequence of this is that if a curve C is closed, i.e. its endpoints are at the same place (e.g. a triangle, a circle, a rectangle, a star shape…) then the integral of a function f with an anti-derivative F along C will be zero. This is because the integral will equal F(w) — F(v), but as v=w this expression is 0. This idea captures that for F, its change in values between points is captured by its derivative, so if we start and finish at the same place, no matter the path we pick, then the integral of its derivative along this path will be 0.

A simple but powerful inequality: the Triangle Inequality

We will also need the triangle inequality. This says that the magnitude of |a+b| is less than |a| + |b|. In essence this is because their directions can cancel (e.g. if a = 1, b = -1, the left side is 0 and the right side is 2). This also holds for complex numbers for a similar reason, but now the magnitude of a complex number is the length of arrow which points to it in the complex plane. In the picture above, |2+3i| = sqrt(2² + 3²) = sqrt(13) as the arrow pointing to 2+3i has length 13. Note that this will hold for adding multiple numbers. So |a+b+c+d| ≤ |a+b+c| + |d| ≤ |a+b| + |b| + |c| ≤ |a| + |b| + |c| + |d|. In the example above, if we let |T*| represent the largest value of |a|, |b|, |c|, |d|, then we would conclude |a+b+c+d| ≤|a| + |b| + |c| + |d| ≤ 4|T*|. We can apply this to integrals: as the output of an integral is a complex number, that means it has a magnitude and we can apply the triangle inequality to sums of integrals.

Statement of the Theorem

The Cauchy-Goursat’s Theorem states that, if we integrate a holomorphic function over a triangle in the complex plane, the integral is 0 +0i. (i.e. both real and imaginary parts of the integral evaluate to 0)

Proof

Step 1: four congurent triangles

We split the triangle into 4 parts, by drawing lines connecting their midpoints

Each of these new triangles has a perimeter one half the size of the original triangle. We define the diameter to be the largest distance between two points, and this also is one half the diameter of the original triangle. This is because the 4 new triangles are congruent to the larger one. If you are interested in a proof of this bit of geometry, see this thread on stackexchange. But hopefully the diagrams make this fact visually obvious!

We now claim that the contours around the four smaller triangles equals that of the larger triangle

Visually that can be seen above. All the paths on the inside cancel (the arrows in the opposing directions) leaving only the path on the outside.

So, we have the following equation, where T is the original triangle, and T_1, T_2, T_3, T_4 represent the 4 smaller triangles,

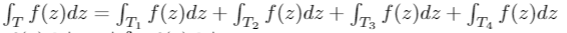
By the triangle inequality (see the end of the previous section on prerequisites), we then get the following. T

In the above T_j represents the triangle whose integral had the largest magnitude. (so the sum of the magnitudes of all four triangles is ≤ 4 times the magnitude of the one with the greatest magnitude.). For example, if the four triangles had magnitudes of 1,5,3 and 2 respectively, then 1+5+3+2 ≤ 5 + 5 + 5 + 5 = 4*5.

Step 2: iterating the first step

Now, we repeat this iteratively: we split the triangle T_j (which was the triangle whose integral had the largest magnitude) into four parts and repeat. After repeating this n times we get

Where T*^n is the nth triangle we picked. In essence, we repeated the first trick, and found a new triangle every single time embedded in the previous one we picked.

It turns out that, as each of these triangles is nested inside the previous (and they are ‘closed’ sets to use the technical lingo), there is a point inside all of them. At this point, we use holomorphism (existence of the complex derivative) at that point. In particular, just like in real calculus, close to the point we can write a linear approximation, with the ‘gradient’ term given by the derivative. That is what we do below.

Here we used holomorphism (I.e. existence of the complex derivative) and we used that the integral of a function with an anti-derivative around a closed curve is 0. (see pre-requisistes section, above).

Step 3: some elementary bounds on the size of integral around the Nth triangle, and looking at the behaviour of these bounds as N gets arbitrarily large.

Now we use our final trick. The magnitude of the integral of f along a curve C is always less than the length of the curve and the maximum magnitude of the function at any point on the curve. For instance, the maximum amount of energy you burn on a run is always less than the length of the route you took multiplied by the max energy burn rate you had during the run. But we know the length of the curve and the maximum distance between two points for the nth triangle.

As n tends to infinity, the final term shrinks to 0, as this was the error term of our expansion: as our triangle gets arbitrarily small, the approximation we did becomes arbitrarily good, and so the error term tends to 0. This leaves one option:

Where we used that a value’s magnitude can only be equal to zero if there is no distance between it and the origin, and thus it is 0.

If you made it this far well done:) hope you enjoyed the proof. I’m moving into the IB mathematics course at cambridge next year. You can follow me on twitter here where I am ethan_the_mathmo. If you are interested in learning complex anlaysis, I recommend the book by Stein and Shakarchi.